Наиболее удобным началом занятий геометриею является установление признания возможности построить прямую линию. Сделать это можно, например, в такой форме. Учащимся раздаются нелинованные тетради и линейки (очень удобно пользоваться бумажными линейками, получаемыми при помощи перегибания куска бумаги, лучше бумаги толстой). Учитель заявляет классу, что он умеет рисовать прямую линию и спрашивает учащихся, умеют ли это делать и они. На основании своего жизненного опыта учащиеся признают за собою это умение, упражняются в рисовании прямых линий при помощи линейки. Здесь явится возможном заменить слово «рисовать» термином «строить». Следует обратить внимание на 2 обстоятельства: 1) отучить учащихся от употребления терминов «косая», «наклонная» и т. п. для называния прямых линий, построенных не параллельно горизонтальному краю доски, – прямая линия остается прямой, как бы ее ни располагали по отношению к привычным для нас предметам; 2) обратить внимание учащихся, что прямая линия видна уже тогда, когда мы только приложим линейку к поверхности доски или тетради, но еще не обвели ее мелом или карандашом, видна, как граница между линейкою и доскою. Далее является возможность установить, что прямую линию можно продолжить, «как хотим, далеко», т. е., что у нее нет концов. Необходимо также, разбирая поверхности различных физических предметов (поверхность доски, поверхность графина, поверхность лица, поверхность яблока) установить, что прямые линии можно строить, без каких-либо ограничений, лишь на особых поверхностях – вводятся термин «плоская поверхность или плоскость» (поверхность доски – «будто плоская поверхность»). Затем учащиеся признают за собой умение строить точки, после чего начинается работа изучения постепенно усложняющихся комбинаций: точка на прямой, прямая и две точки на ней (см. п. 8). Эта работа развивается почти совершенно так же, как то изложено в п. 8. Приходится делать лишь некоторые небольшие отступления для облегчения этой работы, имея в виду, что учащиеся маленькие. Одно из наиболее важных отступлений будет дано ниже. Здесь же необходимо остановиться на одном обстоятельстве. В предыдущем сделан лишь маленький шаг к тому, чтобы учащиеся не смешивали настоящие прямые линии и точки с теми меловыми (или карандашными) чертежами и кружками, которыми они рисуются, – шаг этот имеет место в обращении внимания учащихся, что прямую линию можно видеть, когда она еще не нарисована, а только линейка приложена к доске. Но этого шага мало. Надо выбрать, после того, как уже начались занятия по геометрии, один-два урока для беседы с учащимися по поводу наблюдаемых всюду границ, о трех родах границ и т. д., как это изложено в пп. 8 и 3. Нет сомнений – учащиеся легко понимают содержание такой беседы. Однако, не следует, как к этому привыкли, относиться к этой беседе, как к чему-то такому, что подлежит запоминанию со стороны учеников и что будет с них «спрашиваться» в следующий раз. Нет, беседа так и должна остаться беседою, и лишь иногда в дальнейшем, когда в том встретится надобность, потребуется вспоминать ту или иную часть этой беседы.

То отступление, о котором замечено выше, относится к углам. Учащиеся среди углов выделяют особенный, выпрямленный, замечают, что каждый угол делит плоскость на 2 области, но, пожалуй, преждевременно для таких учащихся разделять углы на меньшие выпрямленного и большие выпрямленного. Приходится, благодаря этому, прибегнуть к приему, который, в сущности, по своей мысли не правилен, а именно – всегда присоединять к углу ту часть плоскости, которую представляется нам возможным уместить целиком на другой (которая «меньше») – этим самым, следовательно, ограничивается работа учащихся лишь углами, меньшими выпрямленных. Конечно, если кто-либо из преподавателей чувствует себя в силе сделать так, чтобы учащимся сделалась ясной возможность присоединять к углу или ту или иную из двух получаемых областей и тем самым ввести сразу в сознание учащихся как углы, меньше выпрямленного, так и углы, большие выпрямленного, то можно только было бы приветствовать такую постановку дела.

Вся работа по усвоению действий над отрезками и углами ведется так же, как то описано в п. 8, за тем лишь исключением, что для перенесения отрезка с одного места на другое приходится употреблять не циркуль, а бумажную линейку, на которой удобно отмечать концы переносимого отрезка карандашом, а для перенесения углов приходится вырезывать из бумаги модель переносимого угла.

Необходимо, помимо сложения и вычитания отрезков и углов, ввести еще деление отрезка и угла пополам. Деление отрезка пополам выполняется при помощи бумажной линейки: концы отрезка отмечаются на линейке, а потом последняя перегибается так, чтобы отмеченные концы совпали. Деление угла пополам выполняется при помощи «угла», вырезанного из бумаги: эта модель угла перегибается так, чтобы стороны угла совпали друг с другом. Учащиеся могут затем получить перегибанием любого куска бумаги модель выпрямленного угла, а вторичным перегибанием разделить выпрямленный угол пополам и получить половину выпрямленного угла или прямой угол. Таким образом в руках у каждого ученика окажется модель прямого угла, и каждый ученик, прикладывая ее к листу бумаги или к доске и обводя стороны этого угла, будет иметь возможность утверждать, что он умеет получать, умеет строить прямой угол.

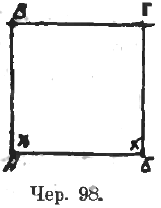
Построение квадрата выполняется в таком порядке (чер. 98): строится отрезок АБ (для начальной школы, чтобы не создавать лишних затруднений, предпочтительнее употреблять для обозначений точек большие русские, а не латинские буквы), при концах его строятся прямые углы (отмечены крестиками), на сторонах этих углов откладываются при помощи бумажной линейки отрезки АВ и БГ, равные отрезку АБ, концы этих отрезков В и Г соединяются отрезков ВГ. Полученной фигуре дается название «квадрат». Изучение квадрата возможно в следующих направлениях: 1) мы строим АБ = АВ = БГ, – возникает вопрос об отрезке ВГ: не равен ли он остальным трем сторонам квадрата? 2 ) Мы строили углы при точках А и Б прямые – возникает вопрос: не прямые ли углы получились и при точках В и Г? 3) Если в предыдущем учащиеся ознакомились до некоторой степени с параллельностью прямых, то возникает вопрос: не параллельны ли стороны АБ и ВГ или АВ и БГ?

По поводу первых двух вопросов имеет место следующее. В сущности, то построение, которое пришлось выполнить для получения квадрата, покоится на симметрии, и если удастся достигнуть того, чтобы ученики чувствовали эту симметрию и осознали, что роль прямой АБ для нашей фигуры совершенно такая же, как и роль прямой ВГ, то тогда должна явится уверенность в том, что 1) ВГ = АБ и что 2) углы при В и Г также прямые. Если же эта симметрия не чувствуется учениками, то придется остановиться только на положении, что, по-видимому, сторона ВГ = АБ (так приблизительно выходит, если сравнивать эти отрезки при помощи бумажной линейки) и что, по-видимому, углы при В и Г прямые (так приблизительно выходит при сравнении этих углов с моделью прямого угла).

Что касается параллельности сторон квадрата, то, если в предыдущем учащиеся были ознакомлены с понятием о параллельных прямых, хотя бы лишь в том смысле, что они смогли представить себе возможность случая, когда две прямые, сколько бы мы их ни продолжали, не пересекаются, и здесь та же симметрия квадрата подскажет учащимся, что надо думать, что противоположные стороны квадрата параллельны.

Совершенно аналогично этому развивается построение и изучение прямоугольника.