Является теперь возможность установить иной взгляд на получение угла: каждый угол можно рассматривать, как результат вращения луча вокруг точки. Если мы имеем луч OA и, отметив его исходное положение, станем его вращать вокруг точки O (по плоскости), то, дойдя, например, до положения OM этого вращающегося луча, получим ∠AOM, являющийся результатом этого вращения (чер. 26).

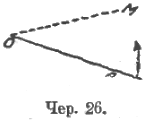
Обратив внимание на какую-либо точку A этого луча OA, мы видим, что эта точка описывает во время вращения луча некоторую линию. Называем ее именем «круг» или «окружность». Так как точки O и A определяют отрезок OA, то устанавливаем возможность получения окружности вращением отрезка около одного из его концов. Строим круг при помощи циркуля (ножки циркуля являются как бы концами воображаемого отрезка) и вводим термины: центр, радиус, диаметр, площадь круга (или окружности), понимая под этим именем часть плоскости, ограничиваемую кругом (или окружностью), дуга и хорда. Является также возможность установить деление всех точек плоскости на точки внутри круга, на круге и вне круга. Легко также явится возможным установить возможность иметь на одном круге равные и неравные дуги.

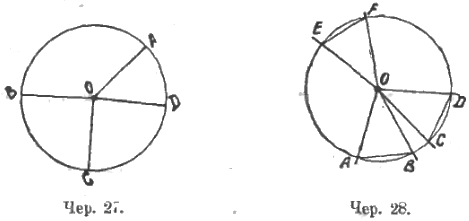
Итак, круг рассматривается нами как линия, которую опишет, например, точка A при вращении отрезка OA около O (чер. 27). Но ясно, что мы получим все то же самое, если начнем вращение с радиуса OB (а не OA) или с радиуса OC или OD и т. п. Это обстоятельство является указанием на полную симметрию круга относительно центра (для учащихся этот род симметрии приходится выражать фразами вроде: «в круге, куда из центра ни смотреть бы, все должно быть одинаковым»). Эта симметрия позволит установить, что если, например, построить в разных местах круга равные хорды (AB = CD = EF …) (а это легко сделать при помощи циркуля, чер. 28) и соединить лучами концы этих хорд с центром O, то получим и равные дуги (◡AB = ◡CD = ◡EF = …) и равны центральные углы (∠AOB = ∠COD = ∠EOF = …). Также ясно, что если удастся построить при центре равные углы, то они высекут из круга равные дуги и определят собою равные хорды, стягивающие эти дуги. Итак, здесь устанавливается ряд положений: равным центральным углам в круге соответствуют равные хорды и равные дуги; равным хордам (или дугам) соответствуют равные центральные углы. Выясняется также, что большему центральному углу соответствует большая дуга и т. п. Подробнее на этом останавливаться не приходится, и тем более не следует из этих положений делать теоремы, подлежащие доказательствам, цель педагогического достижения здесь такова – должно сделать каждому ученику: 1) ясною симметрию круга относительно центра и 2) ясным, что из этой симметрии вытекают вышеуказанные положения.

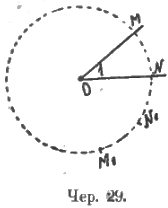
Выясненными свойствами можно пользоваться для построения угла, равного данному, сначала при той же вершине, а затем, когда уяснится (а это делается легко, мимоходом), что круги с равными радиусами равны (конгруэнтны) и при разных вершинах (чер. 29). Пусть имеем ∠1; приняв его вершину за центр, строим круг произвольным радиусом, на этом круге определится дуга MN (или хорда MN, не построенная на чертеже), перенесем при помощи циркуля эту хорду (или дугу) на другое место круга, например, в положение M`N`, соединим концы этой хорды с центром, и мы должны получить угол, равный ∠1. Затем строим круг тем же радиусом, принимая за центр иную точку (а не точку O), после чего является возможным получить угол, равный ∠1 при другой вершине. (В моем курсе (Н. Извольский. – «Геометрия на плоскости») была избрана иная система. Опыт показывает мне предпочтительность системы, излагаемой в настоящей книге; поэтому в 3-м издании «Геометрии на плоскости» я провожу эту систему.) Вводятся упражнения: 1) построить угол, равный данному, при данной вершине так, чтобы одна его сторона шла по данному лучу; 2) построить сумму или разность двух заданных углов (имеющих разные вершины).

Далее, также опираясь на получение круга вращением отрезка, можно установить симметрию круга относительно диаметра: безразлично, вращать ли луч OA для получения круга по стрелке 1 или по стрелке 2 (чер. 30). Отсюда явствует, что части круга, расположенные по разные стороны диаметра AB, тождественны: если плоскость перегнуть по диаметру AB, то одна часть круга совпадет с другою.

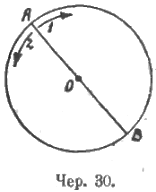
Удобно, напомнив учащимся одну из их любимых забав в детстве (а именно: капнуть несколько капель чернил на лист бумаги, перегнуть его, размазать и, развернув его вновь, получить фигуру, симметричную относительно линии перегиба), здесь установить общее понятие о симметрии фигур относительно оси: если при перегибании плоскости по прямой линии одна часть какой-либо фигуры совпадает с другой, то эта фигура симметрична относительно прямой перегиба или эта прямая (перегиба) есть ось симметрии фигуры. Для круга осью симметрии может служить любой диаметр.

Если рассмотреть теперь фигуры (их можно строить по разному), состоящие из двух кругов, то учащиеся должны суметь найти ось симметрии каждой из этих фигур. Здесь уясняется симметрия точек пересечения двух кругов относительно их линии центров.