К тем сведениям о круге, которые уже имеются у учащихся, прибавляется теперь более подробное изучение вопросов о кругах. Основным вопросом является таковой: мы знаем, что прямая линия определяется двумя точками, – сколькими точками определяется круг? Учащиеся разбирают этот вопрос в таком порядке:
1) Зададим одну точку; сколько можно построить кругов, проходящих через эту точку?
2) Зададим две точки; сколько можно построить кругов, проходящих через эти две точки?
3) Зададим три точки (сначала не на одной прямой, а потом на одной прямой); сколько можно построить кругов, проходящих через эти три точки?
1-ый вопрос приводит к ответу: бесчисленное множество кругов, причем центр можно брать где угодно на плоскости. 2-ой вопрос приводит к ответу: бесчисленное множество, причем центр можно брать только на перпендикуляре к отрезку, соединяющему эти точки, через его середину. 3-ий вопрос приводит к заключению: круг вполне определяется тремя точками, через которые он обязан проходить, т. е., если три точки не лежат на одной прямой, то через них можно построить лишь один круг, а если эти три точки расположены на одной прямой, то через них нельзя построить ни одного круга. При рассмотрении последнего вопроса, когда 3 точки не лежат на одной прямой само-собою приходим к треугольнику, вписанному в круг, и к его свойству.
Дальнейшая работа учащихся должна происходить над вопросом о том, какие различные случаи возможны для расположения прямой и круга. Желательно двоякий подход к этому вопросу 1) закреплены положение прямой и центра круга, а радиус его меняется. Тогда мы видим, что если радиус круга меньше расстояния центра от прямой, то круг не имеем общих точек с прямою, а если радиус круга больше расстояния его центра от прямой, то круг имеет две общих точки с прямою. Намечается особый случай: что будет если радиус круга равен расстоянию его центра от прямой? Обычным путем выясняется, что здесь имеется лишь одна общая точка у круга и прямой, а другой быть не может, и является возможность установить понятие о касании круга и прямой. 2) Закреплен круг (его центр и радиус), а прямая перемещается параллельно самой себе. Здесь также выяснится, что, когда расстояние прямой от центра круга равно радиусу, должен иметь место особый случай, а именно – случай касания прямой и круга.
В результате этой работы явится возможным установить признак касания прямой к кругу (если расстояние прямой от центра круга равно его радиусу, то прямая касается круга), а также построение касательной к кругу через точку, лежащую на самом круге.
После этого явится возможным поставить вопрос, аналогичный основному вопросу: сколькими прямыми определяется круг, если он обязан касаться этих прямых?
Учащиеся устанавливают постепенно: 1) если круг должен касаться одной данной прямой, то таких кругов можно построить бесчисленное множество, причем центр можно брать где угодно на плоскости (здесь намечаются еще побочные вопросы, над которыми могли бы учащиеся поработать, и это очень желательно: каково геометрическое место центров кругов, касающихся данной прямой в данной точке? Каково геометрическое место центров кругов, касающихся данной прямой и имеющих данный радиус?) 2) Если даны две параллельных прямых, то кругов, касающихся этих прямых, можно построить бесчисленное множество, причем центры их расположены на средней параллельной; устанавливается свойство этих кругов: все они имеют одинаковый радиус, равный половине расстояния между данными параллельными. 3) Если даны 2 пересекающихся прямых, то кругов, касающихся этих прямых, можно построить бесконечно много, причем их центры лежат на биссекторах углов, образуемых этими прямыми. 4) Если даны три прямые, из которых две параллельных и третья их секущая, то можно построить 2 круга, касающихся всех трех прямых, причем выясняется особенность этой фигуры: биссекторы двух внутренних односторонних углов пересекаются на средней параллельной. 5) Если даны три прямых, пересекающихся в трех точках, то можно построить 4 круга, касающихся всех трех прямых, причем выясняются свойства треугольника: 6 прямых, делящих пополам и внутренние и внешние углы треугольника, пересекаются по 3 в 4 точках, а именно – в центе вписанного в треугольник круга и в центрах вне-вписанных кругов; биссекторы внутренних углов треугольника пересекаются в одной точке, в центре вписанного круга.
Здесь придется остановиться на понимании термина «определяется», а именно – можно говорить, что круг определяется данными требованиями тогда, когда им удовлетворяет конечное число кругов. Поэтому те требования, которые имеются в задачах 3-ей и 4-ой, определяют круг, т. е. круг (2 или 4 круга) определяется требованием, чтобы он касался трех данных прямых.
Сюда желательно присоединить еще ряд задач на построение само собою возникающих во время работы над предыдущими вопросами: 1) выяснилось, что кругов, касающихся данной прямой в данной точке, можно построить бесконечно много, причем центры их лежат на перпендикуляре к данной прямой через данную точку; не определится ли круг, если к этому требованию присоединить еще одно из разобранных ранее, а именно требование, чтобы круг проходил через другую данную точку? 2) Выяснилось, что требование касаться двух параллельных прямых не определяет положение круга; не определится ли оно, если присоединить сюда еще требование, чтобы круг проходил через точку, данную между параллельными? 3) Выяснилось, что требование касаться двух пересекающихся прямых не определяет положения круга; не определится ли оно, если присоединить сюда еще требование, чтобы круг касался одной из данных прямых в данной точке (если учащиеся придут к мысли взять точку не на одной из данных прямых и потребовать, чтобы круг проходил через взятую точку, то придется указать учащимся, что такая задача может быть решена, но что пока у учащихся недостаточно для этого знаний) или чтобы круг имел данный радиус и т. п.
Далее следует перейти к рассмотрению менее крупных вопросов: 1) изменение хорды в зависимости от ее расстояния от центра; 2) к нахождению оси симметрии фигуры, состоящей из круга и из одной прямой; 3) к решению вопроса, когда у фигуры, состоящей из круга и двух прямых, имеется ось симметрии. Первый из этих вопросов позволит установить, что в круге две хорды равны, если они равно удалены от центра или обратно: равные хорды равноудалены от центра. Второй вопрос приводит к установлению свойства, что диаметр, перпендикулярный к хорде, делит ее пополам. Третий вопрос желательно обработать в такой форме: если построим круг и 2 прямых произвольно, то, вообще говоря, эта фигура не имеет оси симметрии, – возникает вопрос, как надо построить две прямые (или 2 хорды в этом круге), чтобы фигура имела ось симметрии. На этот вопрос изыскиваются ответы: надо или чтобы прямые (хорды) были параллельны или чтобы эти прямые (хорды) были равноудалены от центра.
Затем переходим к изучению фигуры, состоящей из двух кругов. Теперь уже ясно, что 2 круга не могут иметь более двух общих точек (через 3 точки можно построить лишь один круг или даже ни одного). Построив два круга на далеком расстоянии друг от друга и затем постепенно придвигая один к другому, мы с легкостью увидим, какое значение имеют для расположения двух кругов сумма и разность их радиусов и установим соотношения для каждого случая расположения между суммою или разностью их радиусов и расстоянием между их центрами. Здесь, конечно, надо обратить особое внимание на изучение касания кругов и необходимо добиться от учащихся ясных представлений, являющихся ответами на вопросы: много ли можно построить кругов, касающихся данного круга в данной точке? Каково геометрическое место их центров? Каково геометрическое место центров кругов, имеющих данный радиус и касающихся данного круга (внешним или внутренним образом)? Здесь появятся также некоторые конструктивные задачи. Напр.: построить круг, имеющий данный радиус и касающийся данного круга и данной прямой (или двух данных кругов); построить круг, касающийся данного круга в данной точке и проходящей через другую данную точку (следует рассмотреть различные возможные здесь положения точки относительно данного круга). Могут быть введены и более сложные задачи. Напр.: построить круг, касающийся данного круга в данной точке и касающийся данной прямой; построить круг, касающийся данного круга и данной прямой в данной точке; построить круг, касающийся двух данных концентрических кругов и проходящий через точку, данную между ними. Конечно, развитие работы по рассмотрению этих задач зависит и от состава учащихся и от времени.
Уже симметрия круга относительно центра давно позволила учащимся видеть соотношения между центральными углами и высекаемыми ими дугами (если дуги равны, то и центр. углы равны и т. п.). Теперь введем в курс вписанный в круг угол.
Здесь педагогическое достижение должно быть направлено на то, чтобы учащиеся ясно видели (конечно, опираясь на предыдущие сведения), что центральный угол в 2 раза больше вписанного опирающегося на ту же дугу. Надо стремиться, чтобы в сознании учащихся как бы запечатлелась картина, изображенная на чер. 66. Видоизменения расположения центрального и вписанного углов должны быть рассмотрены, но это уже не столь существенно. Главное – добиться запечатления здесь приводимого чертежа.
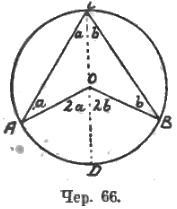
Сюда присоединяется целый ряд существенных вопросов, обычно вводимых в курс в форме теорем. Если окажется, что центральный угол AOB выпрямленный, то вписанный угол будет прямым, а отсюда возникает возможность решить вопрос: много ли можно построить прямоугольных треугольников на данном отрезе, как на гипотенузе? Где расположены вершины этих треугольников? Отсюда переход к построению касательных к кругу из внешней точки. Когда выяснится, что из внешней точки к кругу можно построить 2 касательных, причем их отрезки от этой точки до точек касания равны, то явится возможным разобрать свойство сторон описанного около круга четыреугольника. Здесь возникнет вопрос: нет ли какого-либо аналогичного свойства у вписанного четырехугольника? Интересны следующие сопоставления (чер. 67).
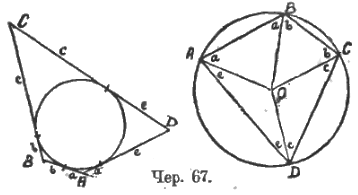
Каждая сторона описанного четырехугольника разбивается точкою касания на 2 отрезка (AB = a + b и т. д.), причем отрезки попарно равны (на первом чертеже равные отрезки обозначены одинаковыми буквами a и a, b и b и т. д.). Каждый угол вписанного четыреугольника разбивается радиусом, проведенным к его вершине, на 2 части (∠A = e + a; ∠B = a + b и т. д.), причем эти части (эти углы) попарно равны (на втором чертеже равные углы обозначены одинаковыми буквами a и a, b и b и т. д.), причем это равенство ясно всякому, кто видит равнобедренные треугольники AOB, BOC и т. д. и знает их свойства. Если на первом чертеже 8 отрезков a, a, b, b, c, c, e и e можно распределить на 2 группы так: AB + CD = a + b + c + e и BC + AD = a + b + c + e, то на втором чертеже 8 углов a, a, b, b, c, c, e и e можно распределить также на 2 группы: ∠A + ∠C = a + b + c + e и ∠B + ∠D = a + b + c + e. Отсюда видно: 1) в описанном четырехугольнике сумма одной пары противоположных сторон равна сумме другой и 2) во вписанном четырехугольнике сумма одной пары противоположных углов равна сумме другой. Если присоединить сюда знание, что сумма внутренних углов всякого четыреугольника равна 4d (четырем прямым), то сумма двух противоположных углов вписан. четыреуг-ка равна 2d. Аналогичного добавления для описанного четыреугольника сделать нельзя, ибо сумма всех сторон (периметр) четыреугольника может меняться до бесконечности, и это желательно сделать ясным для учащихся.
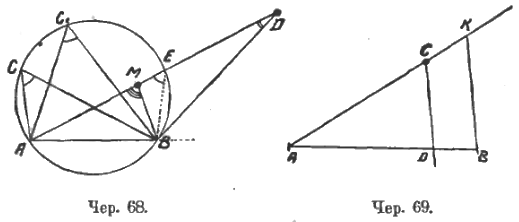
Возможность построить множество вписанных углов, высекающих из круга одну и ту же дугу (или, как обычно говорят, опирающихся на одну и ту же дугу) и возможность видеть их равенство (каждый из них равен половине одного и того же центрального угла) приводит к задаче: построить геометрическое место точек, из которых данный отрезок виден под данным углом. Этой задаче должен предшествовать следующий разбор (чер. 68): из всякой точки дуги AC1B (напр., из C, из C1 и т. д.) хорда AB видна под равными углами, а из любой точки вне круга (но по ту же сторону прямой AB), напр., из точки D, под меньшим углом (видно из ∆EDB: ∠AEB внешний, а ∠D внутренний), а из точки M внутри круга – под большим углом (видно ∆MEB: ∠AMB внешний, а ∠AEB внутренний). Когда таким образом выяснится, что искомое геометрическое место точек, из которых данный отрезок должен быть виден под данным углом, есть дуга некоторого круга, проходящего через концы отрезка (точнее: дуги двух кругов, причем одна дуга лежит по одну сторону прямой AB, а другая по другую сторону), можно приступить к самому построению. Учащимся ближе и понятнее такое построение (чер. 69): пусть AB – данный отрезок и ∠m – данный угол. Построим через A любой луч и на нем возьмем любую точку C. Построим при C ∠ACD = ∠m. Тогда из точки C виден под углом m не данный отрезок AB, но лишь его часть, а именно отрезок AD. Найдем теперь на луче AC такую точку, чтобы из нее был виден под данным углом весь отрезок AB, для чего надо через т. B построить BK || DC. Тогда из точки K отрезок AB будет виден под данным углом – остается через 3 точки A, K и B построить круг, что умеем выполнять. Можно присоединить сюда несколько задач на построение, решение которых основано на изучаемом геометрическом месте.
Не будем останавливаться на подробностях этой части курса, а лишь заметим, что возможно по ходу дела изменить порядок. Напр., возможно сначала изучать геометрическое место точек, из которых данный отрезок виден над данным углом, отсюда перейти к вписанному в круг четыреугольнику, а затем к построению касательной к кругу из внешней точки и к описанному четыреугольнику.
