Развитие соображений о равенстве площадей представляет собою ценный материал для приучения учащихся к обобщающей работе мысли, а потому оно никоим образом не должно комкаться так, как это обычно имеет место в наших ходовых учебниках.
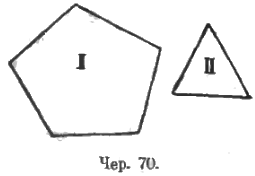
Прежде всего тот процесс наложения, который неоднократно имел место в предыдущем, позволит учащимся установить, что две площади следует считать равными, если они при наложении совпадают. Далее ставим на очередь вопрос о сложении двух площадей (напр., I и II), ограниченных прямыми линиями (чер. 70). В основе сложения лежит, как мы уже знаем, процесс сдвижения, а здесь мы можем две наших площади (I и II) сдвинуть множеством различных способов. Следует, чтобы учащиеся выполнили (при помощи циркуля и линейки), по крайней мере, два различных построения нахождения суммы I и II площадей, которые в результате давали бы 2 площади, не совпадающие между собою при наложении. Учащиеся уже знают переместительный закон сложения для чисел, для отрезков, для углов – теперь становится необходимым обобщить этот переместительный закон и принять, что, как бы мы ни придвинули одну площадь к другой, результаты этих сдвижений должны считаться равными. Обратив хотя некоторое внимание на сложение трех и более площадей (а, следовательно, и на обобщение свойства сложения, что при сложении многих слагаемых их можно складывать любыми группами и в любом порядке, – а это свойство является следствием переместительного и сочетательного законов), мы приходим к установлению второго признака равенства площадей: две площади (ограниченные прямыми) должны считаться равными, если каждая из них является суммою площадей, попарно совпадающих при наложении (здесь, в сущности, имеется еще одно обстоятельство: каждая площадь должна считаться суммою конечного числа слагаемых).
Переходим к вычитанию площадей. Опять видим (применяясь, напр., к I и II площадям), что это вычитание можно выполнить разнообразными способами, что влечет за собою новый признак равенства площадей: две площади должны считаться равными, если каждая из них есть разность площадей, совпадающих при наложении.

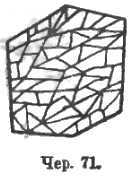
Как известно, наука устанавливает 3 разных термина для этих трех случаев равенства площадей: 1) равенство по наложению – конгруэнтные площади, 2) равенство по сложению – равносоставленные площади и 3) равенство по вычитанию – равновеликие площади. Здесь возникают тонкие вопросы, и, быть может, должно об них побеседовать с учащимися: 1) не могут ли две равносоставленные площади быть не равными по наложению, т. е. пусть некоторая площадь разбита на много (но не на бесконечно большое число) слагаемых (чер. 71), – нельзя ли эти слагаемые площади переложить так, чтобы из них получилась новая площадь, явно не совмещающаяся с начальной, напр., чтобы вся новая площадь умещалась внутри начальной или, наоборот, чтобы новая площадь закрывала всю начальную, да еще захватывала бы какой-либо кусок плоскости, лежащий вне начальной? 2) Обязательно ли две равновеликие площади в то же время и равносоставлены? Другими словами: две площади, равные по вычитанию, должны ли быть равными и по сложению? Смысл этих вопросов сводится, конечно, к общему вопросу: не может ли оказаться противоречий при применении трех вышеустановленных признаков равенства площадей? Эти вопросы послужили предметом научных изысканий (принцип Де-Цольта, теория площадей Гильберта), но знакомить учащихся с этими изысканиями не представляется возможным, и приходится ограничиваться лишь тем, что эти вопросы не должны замалчиваться перед учащимися. Последние, на основе своих непосредственных представлений, приходят к установлению отсутствия противоречий в трех вышеуказанных признаках равенства площадей и, следовательно, к заключению:
Две площади равны: 1) если они совпадают при наложении и 2) если каждая из них является суммою или разностью площадей, совпадающих попарно при наложении.
Установленные признаки для применения к площадям понятий «больше» или «меньше» не представляет трудности.
Основные проекты учения о равновеликости многоугольников (два многоугольника называют равновеликими, если равны их площади) таковы: 1) равновеликость двух параллелограммов с равными основаниями и высотами (следует указать на возможность видеть, что площади таких параллелограммов равны и по вычитанию и по сложению); 2) равновеликость треугольников, имеющих равные основания и равные высоты; 3) превращение треугольника в равновеликий прямоугольник, четыреугольника – в треугольник, пятиугольника (и т. д.) – также в треугольник; 4) теорема Пифагора.
Лучшим способом выяснения теоремы Пифагора считаю, согласно свой практике, следующий.
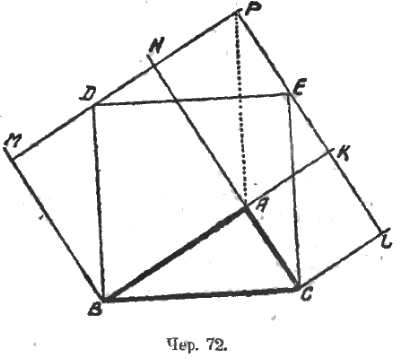
Предлагаем учащимся выполнить следующее (сложное) построение. Строим (чер. 72):
1) прямоугольный треугольник BAC (∠A = d).
2) Квадрат BDEC на гипотенузе BC (BD ⊥ BC, CE ⊥ BC, BD = EC = BC).
3) AK – продолжение BA, CL || AK и прямую EL (через точку E) || AC – получится квадрат CAKL на катете AC (для выяснения этого придется рассмотреть ∆ECL и ∆BAC; у них BC = EC и ∠BCA = ∠ECL; так как эти треугольника прямоугольные, то этого достаточно, чтобы быть убежденным в их равенстве, т. е. ∆ECL = ∆BAC).
4) AN – продолжение CA, BM || AN и прямую MDN (через точку D) || BA – получим квадрат BMNA на катете BA (выясняется это при помощи равенства треугольников BMD и BAC).
5) NP – продолжение MN и KP – продолжение LK; наконец, – прямую PA.
Тогда получим еще 3 треугольника, равных начальному, а именно: ∆DPE, ∆ANP и ∆PKA.
Итак, имеем: ∆ABC = ∆CEL = ∆BDM = ∆DPE = ∆ANP = ∆PKA.
Мы видим, что придется от всей застроенной площади BMPLCB отрезать 3 куска, а именно: площади треугольников BMD, DPE и CEL, чтобы получить площадь квадрата BDEC. Но у нас имеется 6 равных треугольников; если от застроенной площади BMPLCB отрезать площади остальных трех треугольников (т. е. ∆BAC, ∆ANP и ∆PKA), то получим площади двух квадратов ABMN и AKLC, откуда и приходим к выводу, что площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.
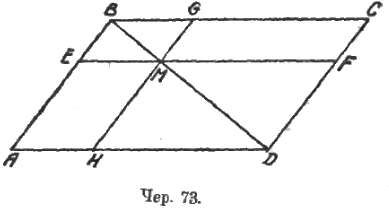
Очень хорошо ввести в дело и знаменитое евклидово построение (чер. 73), дающее возможность получить 2 равновеликих параллелограмма, имеющих и разные стороны и разные высоты, но равные углы. Это построение таково. Строим: 1) параллелограмм ABCD, 2) его диагональ BD, 3) через любую точку M его диагональ BD две прямые: EF || BC и GH || BA.
Тогда легко видеть:
1) площадь AEMH = площади MGCF и
2) площадь ABGH = площади EBCF.
Это построение можно применить к решению ряда вопросов и задач (см. приложение), а с учащимися его следует использовать для превращения данного прямоугольника в другой, равновеликий ему и имеющий данное основание. Это важно потому, что таким образом видно, что для решения этой задачи не надо ни умения измерять площади, ни знания пропорциональности отрезков (при обычном решении этой задачи всем этим пользуются).
