На чер. 73 дано построение равновеликих параллелограммов, имеющееся у Евклида. Этим построением можно пользоваться для решения различных задач на превращение параллелограмма или прямоугольника в равновеликий ему, удовлетворяющий известным требованиям.
Например, легко решается, без сведения дела к измерению, задача: построить прямоугольник, равновеликий данному и имеющий данное основание (обычно, опираясь на знание того, что площадь прямоугольника равна произведению основания на высоту, задачу сводят к построению 4-го пропорционального отрезка).
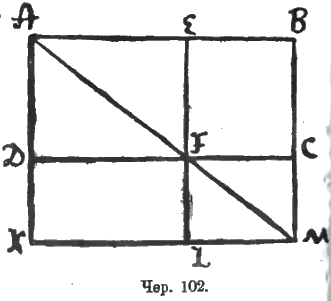
Решение этой задачи, без сведения к алгебре, таково: пусть ABCD (чер. 102) – данный прямоугольник; отложив отрезок AE, равный данному основанию искомого прямоугольника, и состроив EL || AD, а заем прямую AF, где F точка пересечения EL с DC, и построив MK || BA (точка M есть точка пересечения BC и AF), получим прямоугольник ABMK, для которого видим, что прямоугольник AELK имеет данное основание AE и равновелик данному прямоугольнику ABCD.
Это решение задачи было давно известно, хотя и не пользуется распространением. Под его влиянием может возникнуть мысль изыскать решение, построенное на той же идее, другой общеизвестной задачи: построить квадрат, равновеликий данному прямоугольнику.
Предварительно надо ознакомиться с так называемой «прямой Симсона».
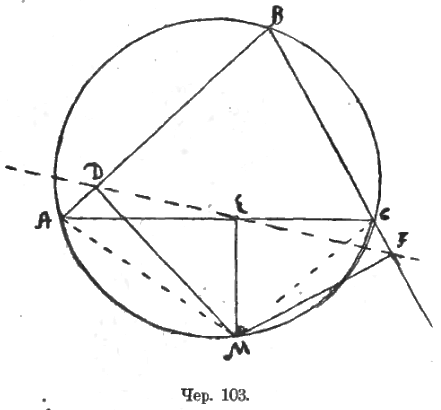
Если в круг вписан треугольник ABC (чер. 103) и если из какой-либо точки M окружности построены перпендикуляры MD, ME и MF на его стороны, то, как известно, основания этих перпендикуляров, точки D, E и F, лежат на одной прямой, называемой «прямая Симсона».
Вот выяснение этого.
Угол ADM – прямой; следов., точка D лежит на окружности, диаметром которой служит отрезок AM. Так как ∠AEM тоже прямой, то точка E лежит на той же окружности. Поэтому углы AMD и AED суть углы, вписанные в эту окружность и опирающиеся на одну и ту же дугу AD (она на чертеже не дана). Следов., ∠AED = AMD.
Так как ∠MEC = d и ∠MFC = d, то точка E и F лежат на окружности, диаметром которой служит отрезок MC, и углы CMF и CEF суть вписанные в эту окружность и опирающиеся на одну и ту же дугу CF (не нарисованную на чертеже). След., ∠CEF = ∠CMF.
Так как четырехугольник MABC вписан в круг, то ∠AMC + ∠B = 2d.
Так как углы при точках D и F в четырехугольнике MDBF прямые, то этот четыреугольник есть вписываемый и, следов., ∠DMF + ∠B = 2d.
Отсюда мы выводим, что ∠AMC = ∠DMF. Так как ∠AMC = ∠AMD + ∠DMC и ∠DMF = ∠DMC + ∠CMF, то отсюда имеем:
∠AMD + ∠DMC = ∠DMC + ∠CMF
или
∠AMD = ∠CMF.
Но мы получили, что ∠AED = ∠AMD и ∠CEF = ∠CMF. Следов., ∠AED = ∠CEF.
Так как AEC есть прямая линия, то равенство углов AED и CEF указывает на то, что DEF есть также прямая линия.
Известна и обратная теорема: если из какой-либо точки плоскости треугольника опущены перпендикуляры на его стороны и если их основания расположены на одной прямой, то указанная точка расположена на окружности, описанной около треугольника.
Выяснение этого немного отличается от предыдущего. Мы теперь не знаем, что четыреугольник ABCM есть вписываемый, но зато знаем, что DEF есть прямая и, следовательно, ∠AED = ∠CEF. Так как по-прежнему точки A и E лежат на окружности, диаметром которой служит отрезок DM, и точки E и F лежат на окружности, диаметром которой служит отрезок MC, то по-прежнему имеем: ∠AED = ∠AMD и ∠CEF = ∠CMF.
Отсюда заключаем, что ∠AMD = ∠CMF. Так как четыреугольник MDBF по-прежнему вписываемый (ибо углы при D и F прямые), то ∠DMF + ∠B = 2d или ∠DMC + ∠CMF + ∠B = 2d или ∠DMC + ∠AMD + ∠B = 2d или ∠AMC + ∠B = 2d, откуда и заключаем, что точка M лежит на круге, описанном около ∆ABC.
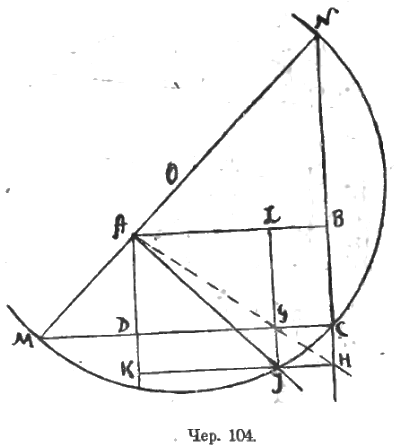
Пусть ABCD (чер. 104) есть данный прямоугольник и ALJK – искомый квадрат. Тогда вершина J этого квадрата должна лежать на биссекторе AJ прямого угла A данного прямоугольника. Далее искомая точка J должна занять на этом биссекторе такое положение чтобы точка A, G и Н лежали на одной прямой. Точки G и H суть основания перпендикуляров, опущенных из точки J на прямые DC и BC. Тогда возникает мысль применить сюда «прямую Симсона». Примем прямые DC и BC за 2 стороны треугольника, третьею же его стороною должна быть прямая, перпендикулярная к AJ. Эта прямая MN легко строится. Получим ∆MCN. Центр O этой окружности (ибо ∠MCN прямой) должен лежать в середине отрезка MN. Раз точка J определена, то построение квадрата KJLA не вызывает затруднений.
Та же идея может быть применена к задаче деления отрезка в крайнем и среднем отношении. Если дан отрезок AB, то задача сводится к разделению этого отрезка на такие две части AL и LB, чтобы квадрат, построенный на большей из них, на отрезке LB, был равновелик прямоугольнику, сторонами которого служат сам отрезок AB и другая часть его, именно AL.
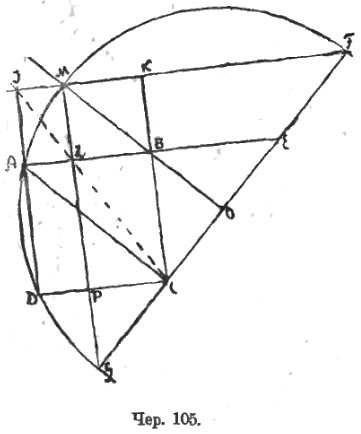
Пусть (чер. 105) квадрат LMKB равновелик прямоугольнику ALPD, причем AD = AB. Продолжив стороны этого квадрата и прямоугольника, получим прямоугольник DJKC и квадрат DABC, причем точки C, L и J должны лежать на одной прямой, на диагонали прямоугольника DJKC. Построив диагональ AC, мы увидим, что точки J, L и C можно рассматривать, как основания перпендикуляров, построенных из точки A на стороны ∆GMF, причем сторона GF есть прямая , перпендикулярная к AC. Из этого следует, что ∠DCG = 45°, а, следовательно, ∠MGC = 45° и ∠MFG = 45°. Также ∠BCE = ∠BEC = 45° (точка E есть точка пересечения продолжения AB с прямою GF).
Точка A должна лежать, согласно обратной теореме о «прямой Симсона», на окружности, описанной около ∆GMF, а центр O этой окружности должен лежать на середине отрезка CE, откуда вытекает построение для определения точки M: 1) строим на AB квадрат ABCD и его диаг. AC, 2) строим через точку C прямую GF ⊥ AC, – тогда определится точка E, 3) делим отрезок CE пополам в точке O, 4) строим прямую через O и B, – эта прямая образует со сторонами BC и AB углы в 45° (ибо ∆CBE равнобедренный), 5) строим окружность, принимая точку O за центр и OA (или OD) за радиус, – пересечение этой окружности с прямою OB определит точку M. Раз точка M определена, то построив MLP ⊥ AB, соединив M с F и продолжив CB до пересечения в точке K с MF, получим квадрат LMKB (так как диагональ BM составляет со сторонами BL и BK углы по 45°), равновеликий прямоугольнику ALPD, что и дает решение задачи.
