Статья о правильных многоугольниках не требует особых методических указаний. Ограничусь лишь немногими замечаниями.
1. Исходным пунктом может явиться вопрос: мы умеем построить равносторонний треугольник и квадрат; они обладают особенностью, – у них равны все стороны и все углы между собою; нельзя ли построить многоугольник с большим числом сторон, обладающий тою же особенностью?
2. При изучении правильного десятиугольника на первый план должно выдвинуть построение стороны правильного десятиугольника, а не ее вычисление.
3. Формулы 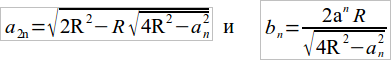 в сущности, для курса ненужны, и их можно заменить несколькими частными задачами: вычислить a12 или b6 (зная, что a6 = R); вычислить a8 и b8 (зная, что a4 = R√2). Во всяком случае, общие формулы могут появиться в курсе только после вышеуказанных примеров.
в сущности, для курса ненужны, и их можно заменить несколькими частными задачами: вычислить a12 или b6 (зная, что a6 = R); вычислить a8 и b8 (зная, что a4 = R√2). Во всяком случае, общие формулы могут появиться в курсе только после вышеуказанных примеров.
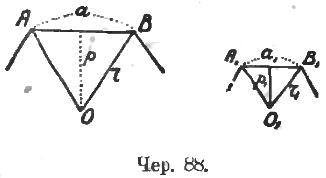
4. Пропорциональность периметров двух одноименных правильных многоугольников их радиусам или апофемам можно получить из подобия треугольников (чер. 88) и нет нужды ссылаться на подобие многоугольников. Если 2 правильн. многоугольника имеют по одинаковому числу сторон (n), то ∆OAB подобен ∆O1A1B1 и из них:
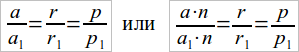
Вопрос об определении длины круга принадлежит к числу сложных вопросов, – по его поводу не мало написано статей в различных журналах.
Обычное изложение требует, мотивируя это требование желанием придать изложению формальную строгость обосновать вопрос об определении длины окружности и площади круга при помощи теории пределов, для чего в учебниках геометрии посвящается целая глава изложению начал теории пределов. Однако, возникают большие сомнения и в том, удается ли при таком способе достигнуть желаемой строгости, и в том, не слишком ли отодвигается на задний план сущность дела тем, что на первый план выдвигается формальная сторона изложения, на которую должно быть направлено внимание учащихся. По моему глубокому убеждению, теория пределов бессильна в этом вопросе и не может охватить сущность дела. Все эти сомнения мною изложены в брошюре – «К вопросу об определении длины окружности», материалом для которой явился мой доклад под тем же заглавием, прочитанный на 2-м Всероссийском Съезде преподавателей математики. (См. «Доклады, читанные на 2-м Всероссийском Съезде препод. математики», стран. 186 и т. д.) Здесь не место излагать все относящиеся сюда соображения, а необходимо лишь указать ту систему прохождения этой части курса, которая, с одной стороны, по возможности упрощала бы дело, а с другой, по возможности, выдвигала бы суть дела на первый план.
Исходным пунктом, без чего нельзя и ставить вопроса об измерении длины окружности, является всеми отчетливо сознаваемое представление о возможности, как бы перерезав окружность, выпрямить ее, – получаемый таким образом в представлении прямолинейный отрезок и есть длина круга. (Мы употребляем на равных правилах выражения: «длина окружности» или «длина круга», «площадь окружности» или «площадь круга» (см. гл. 6). В гл. 10 выяснено, что термины «круг» или «окружность» здесь употребляются, как синонимы.) Заменять это отчетливое представление словесным определением – «длиною окружности называется предел, к которому стремится периметр правильного вписанного (или описанного) многоугольника при безграничном увеличении числа его сторон» – значит впадать в схоластику, и такая замена является с педагогической точки зрения большим грехом. С точки зрения истинной науки (а не схоластики) тут оказывается пробел, который восполнить, по-видимому, нельзя, а именно игнорируется выяснение того, совпадает ли это словесное определение с имеющимся в нашем сознании представлением о длине круга.
Далее вопрос развивается в таком порядке. Мы не обладаем способом построения такого прямолинейного отрезка, который заведомо был бы равен выпрямленному кругу. Поэтому мы не имеем возможности выполнить измерение длины круга линейною единицею прямо, а принуждены искать косвенные способы. Таких способов намечается два. 1. Мы можем взять какой-либо многоугольник (лучше правильный), вписанный в круг, и выпрямить его периметр. Получим определенный отрезок. Этот отрезок имеет определенную близость к «длине круга», и эта близость тем больше, чем больше вершин многоугольника лежит на окружности. Отсюда возникает мысль о возможности для целей измерения рассматривать круг как правильный многоугольник с бесконечно большим числом сторон.
2. Мы можем начать с выпрямления периметра правильного описанного около круга многоугольника и, увеличивая число его сторон, также прийти к той же мысли, что мы можем для целей измерения рассматривать круг, как правильный многоугольник с бесконечно большим числом сторон.
Нет, конечно, надобности педантично избегать и слова «предел», и учащиеся могут установить, что длину окружности можно рассматривать, как предел для изменяющегося выпрямленного периметра правильного вписанного (или описанного) многоугольника при бесконечном увеличении числа его сторон.
Если позволяет время, то этот вопрос можно рассмотреть более подробно: 1) можно установить, что выпрямл. периметр каждого вписанного многоугольника меньше периметра любого описанного; 2) можно установить возможность построения двух правильных многоугольников, вписанного и описанного, разность периметров которых меньше любого наперед заданного отрезка; 3) можно, откладывая ряд периметров и вписанных и описанных многоугольников на прямой от определенной точки, прийти к заключению, что длину круга следует считать как бы границею между множеством отрезков, выражающих выпрямленные периметры вписанных многоугольников, и множество отрезков, выражающих периметры описанных многоугольников. Такой граничный отрезок является возможным рассматривать, как выпрямленный периметр прав. вписанного или описанного многоугольника с бесконечно большим числом сторон.
Такое подробное развитие дано (мелким шрифтом) в моем курсе «Геометрия на плоскости». Однако, на практике с учениками приходится довольствоваться только тем, что 1) учащиеся признают, согласно своим представлениям, возможность рассматривать круг, как правильный многоугольник с бесконечно большим числом сторон и 2) учащиеся признают возможность рассматривать два круга, как правильные одноименные (хотя и с бесконечно большим числом сторон) многоугольники. Отсюда вытекает возможность признать справедливою пропорциональность их периметров (или «длин» этих кругов) их радиусам или диаметрам, откуда и явится переход к числу π.
По поводу числа π необходимо установить, что его легко вычислить с точностью до единицы, а именно: легко получить, с помощью прав. описанного шестиугольника и описанного четыреугольника, что
3 < π < 4.
Полагаю, что совершенно излишняя трата времени будет иметь место в том случае, если учащихся привлекают к вычислению числа π с большей точностью. Достаточен тот результат, который получается от вычисления с точностью до 1 и от сознания, что можно при помощи правильных вписанных и описанных многоугольников вычислить число π с большею точностью, для чего лишь придется проделать целый ряд (и иногда утомительных) вычислений.
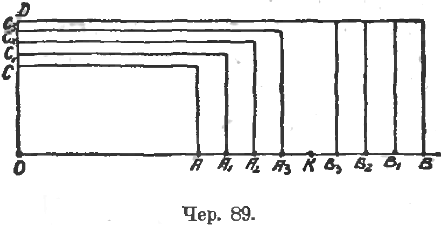
По отношению к измерению площади окружности наиболее тонким вопросом является следующий: площадь круга, будучи больше площади любого вписанного многоугольника и меньше площади любого описанного многоугольника (это непосредственно ясно), является общею границею между площадями вписанных и описанных многоугольников (чер. 89). Если на прямой откладывать выпрямленные периметры прав. вписанных многоугольников OA, OA1, OA2 … и периметры правильных описанных многоугольников OB, OB1, OB2 … с постепенно увеличивающимся числом сторон, то границею между ними явится некоторый отрезок OK, представляющий собой длину круга. Если затем строить прямоугольники CA, C1A1, C2A2 …, равновеликие площадям вписанных прав. многоугольников (след., OC, OC1, OC2 … суть их апофемы) и ряд прямоугольников DB, DB1, DB2 …, равновеликих площадям описанных прав. многоугольников (след., OD = радиусу круга), то должен существовать некоторый граничный прямоугольник с прямоугольником DK, основанием которого служит отрезок OK, представляющий длину круга?
Подобные соображения по поводу этого вопроса изложены в вышеуказанных брошюре и докладе – «К вопросу об определении длины круга». В классе в громадном большинстве случаев придется ограничиться тем, что раз мы пришли к мысли о возможности рассматривать круг, как правильных многоугольник с бесконечно большим числом сторон, то и измерение его площади можно выполнять так же, как площади правильного многоугольника, т. е. придется измерить его периметр (т. е. длину круга), измерить его апофему (т. е. радиус круга), перемножить полученные числа и разделить на 2.
Важными упражнениями здесь являются вопросы: во сколько раз увеличится площадь круга, если го радиус увеличится в 2 раза? в 3 раза? и т. д.
Вот схема таких упражнений.
Пусть радиус = 1 дм.; тогда площадь круга = π кв. д.

