Выделяя в особую часть учение об измерении геометрических объектов, «измерительную геометрию», я вовсе не хочу этим сказать, что в предыдущем учащихся должно было отводить от всяких измерений в области геометрии. Нет, если на протяжении предыдущего курса появятся моменты, когда целесообразно ввести в дело измерение (напр., в вопросе об относительном расположении двух кругов), то всегда преподавателю явится возможность предложить учащимся соответствующие упражнения. Однако, там на это измерение учащиеся могли смотреть лишь с той точки зрения, какая имеет место в житейской практике: усложнить несколько раз какую-либо единицу меры (напр., сажень), приложить к измеряемому объекту, напр., фут, разделенный на дюймы и линии, или транспортир, разделенный на градусы, и отсюда получить соответствующее число для измеряемого объекта. Но должен наступить момент, когда процесс измерения явится возможным выяснить с теоретической точки зрения и воспользоваться им для убеждения учащихся в необходимости вдумчивого отношения к тому, что на практике мы выполняем как бы машинально. Такой момент наступает, согласно моим наблюдениям, в 5-м или 6-м классах средней школы. И вот, настоящая глава имеет целью уяснить до возможной отчетливости «процесс измерения».

Учащиеся вспоминают, что они измеряли в свое время длину комнаты, высоту дерева и т. п., причем результаты этих измерений записывали в виде:

длина комнаты = 11 аршин
высота дерева = 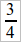сажени и т. п.

В каждой из этих записей входят 2 прямолинейных отрезка (ведь под именем «длина комнаты» мы представляем себе некоторый отрезок, так же точно под именем «аршин» и т. п.) и число. Под влиянием этих воспоминаний мы приходим к общей мысли: если под именем a и b понимаем 2 прямолинейных отрезка и если о них записано, что a = kb, где k означает какое-либо число, то мы можем смотреть на эту запись, как на результат измерения отрезка a отрезком b (или: принимая за единицу отрезок b).

Сначала полезно поработать с учащимися над уравнениями того вида, который имеется выше, т. е. над уравнениями вроде y = 7x или 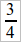и т. п.

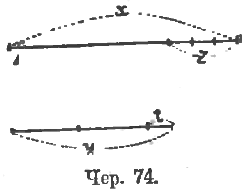
Учащиеся должны ясно представить себе: 1) что каждое из этих уравнений имеет бесчисленное множество решений в числах, причем эти решения можно получить, давая x – y произвольное значение и вычисляя соответствующее значение для y – a; 2) каждое из этих уравнений имеет бесчисленное множество решений в отрезках, причем для получения этих отрезков надо принять определенный отрезок для x и затем построить соответствующий отрезок для y. Далее возникает обратная задача: даны 2 отрезка x и y (чер. 74); составить для них уравнение рассматриваемого вида, т. е. вида x = ky (или y = k'x), где k (или k') число. Эту задачу, в согласии с предыдущим, и должно формулировать: «измерить отрезок x отрезком y» (или наоборот: измерить отрезок y отрезком x). Таким образом на вопрос, что значит измерить отрезок a, принимая за линейную единицу отрезок b (или короче: «отрезком b»)? Следует отвечать: «это значит – составить для этих отрезков уравнение вида a = kb, где k какое-либо число».

Итак, пусть требуется измерить отрезок x отрезком y (см. выше данный чертеж). Решение само собою намечается в такой форме: попытаем, не уложится ли отрезок y на отрезке x несколько раз без остатка; если бы это случилось, то сразу получили бы уравнение желаемого вида x = ky. Применяясь к чертежу, видим, что эта попытка не удается; тогда намечается возможность новой попытки: не уложится ли остаток z на отрезке y без остатка – тогда тоже явится возможность составить желаемое уравнение. Продолжаем эти попытки дальше... мы видим, что задача будет решена лишь тогда, когда окажется, что какой-нибудь остаток уложится на предыдущем без остатка. Поэтому делаем допущение: положим (это допущение сделано применительно к нашему чертежу), что отрезок t укладывается на отрезке z ровно 3 раза, т. е. имеем:

x = y + z
y = 2z + t
Пусть z = 3t

Отсюда обычным путем получаем:

y = 7t; x = 10t и .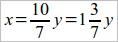

Итак, задача решена – искомое уравнение составлено. Теперь видно (и это надо сделать именно теперь, а не раньше, как то обычно делают учебники геометрии), что в решении вопроса сыграл важную роль отрезок t. Учащиеся видят: 1) отрезок t укладывается, согласно предположению, по целому числу раз и на x и на y – отсюда является возможность установить общее понятие об общей мере двух отрезков; 2) решить задачу удалось только благодаря предположению, что процесс отложения нового остатка на предыдущем заканчивается (и тем самым получается общая мера данных отрезков) – отсюда является возможность установить понятие о соизмеримых и несоизмеримых отрезках.

Учащиеся после упражнений, приобретают навык в измерении одного отрезка другим, в предположении их соизмеримости, т. е. в составлении уравнений вида y = kx, где y и x – отрезки, а k – целое или дробное число.

На протяжении этих упражнений следует обратить внимание на то, что уравнение y = kx, где и y и x и k числа, может быть представлено в форме 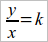, причем оно тогда читается так: отношение числа y к числу x равно числу k. Полезно расширить эту возможность и условиться так же писать наше уравнение и тогда, когда y и x не числа, а отрезки – этим условием как бы устанавливается определение деления одного отрезка на другой. Учащиеся должны понять, что и уравнение y = kx и уравнение  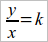выражают одну и ту же зависимость между отрезками и разнятся друг от друга не по существу, а по форме. Учащиеся в упражнениях для каждой данной пары отрезков (предполагающихся соизмеримыми) получают обе формы искомой зависимости и легко осваиваются с мыслью, что из одной формы этого уравнения непосредственно вытекает другая.

Далее берем 2 отрезка (a и b – чер. 75) и делаем предположение, что они несоизмеримы.

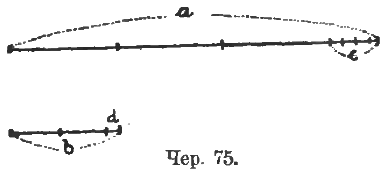
Тогда, применяясь к нашему чертежу, получим при помощи того же процесса отложения:

a = 3b + c
b = 2c + d
3d < c < 4d
или: c = приблизительно 3d или 4d.

Последние 2 строчки имеют такое происхождение: так как a и b несоизмеримы, то никогда мы не можем дойти до конца; поэтому остановимся где-нибудь и составим наше уравнение лишь приближенно верное (как мы это и делаем постоянно в практических измерениях). Из последнего отложения (d на c) мы, в сущности, видим, что c > 3d и что c < 4d (или: 3d < c < 4d), но приблизительно мы можем принять, что c = 3d (отбрасывая остаток) или что c = 4d (считая этот остаток за целый отрезок d).

Теперь переходим к вычислениям, которые раздваиваются.

1) Пусть c = 3d (прибл.) тогда
b = 7d
a = 24d и

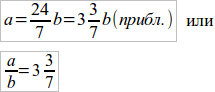
2) Пусть c = 4d (прибл.) тогда
b = 9d
a = 31d и

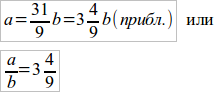
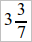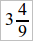Так как по настоящему c заключается между 3с и 4c, то и истинный результат измерения должен заключаться между полученными числами и . Надо выяснить, какое из них больше: 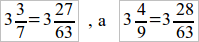– т. е.  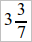<  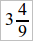(если бы мы продолжили еще один раз процесс наложения, то оказалось бы наоборот: число, полученное в 1-м абзаце вычислений, больше числа, полученного во 2-м. Учащимся, не знающим непрерывных дробей, это кажется странным, и их надлежит освоить с этим фактом, не задаваясь целью достаточно ясно осветить его происхождение).

Тогда мы имеем право записать:

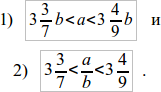
Вероятно, к этому времени учащиеся уже встречались с подобными записями в курсе алгебры при изучении корней (напр., 1,41 < √2 < 1,42) и знают, что если написано

m < √a < n,

то эту запись можно понимать в смысле: √a вычислен с точностью до (n – m), т. е., если принять √a = m или √a = n, то в обоих случаях ошибка окажется меньше числа n – m.

Так точно и здесь. Получив выше данные записи, мы можем установить:

Отсюда получаем и общий результат: если отрезки a и b несоизмеримы, то их отношение не может быть выражено безошибочно ни целым числом, ни дробным, но зато может быть выражено приближенно с определенною точностью. Придется лишь указать учащимся, что если бы они ознакомились с «непрерывными дробями», то могли бы находить это отношение с какою угодно заданною степенью точности. Получается положение, аналогичное тому, какое имело место в курсе алгебры при рассмотрении корней вроде и т. п. Имеется, следовательно, и здесь возможность установить необходимость введения понятия о новом числе – иррациональном. Итак, мы должны считать, что истинное отношение отрезка a к отрезку b есть какое-то иррациональное число – назовем его через k'. Тогда

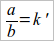и a = k' ∙ b.

Это иррациональное число k' мы можем вычислить с любою степенью точности.

Если даны два отрезка x и y, то при помощи их определяется число k (или целое или дробное или иррациональное), удовлетворяющее уравнению

x = ky или .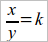

Это число может быть обозначаемо особым знаком (у нас буквой k) или при помощи самих отрезков, а именно символом .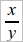

Чтобы приучить к этим символам, возможен ряд упражнений вроде:

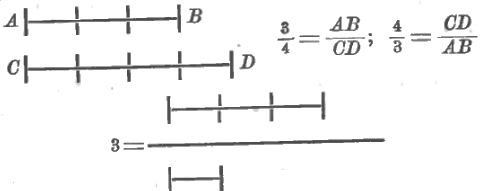
(число 3 есть отношение двух отрезков, которые непосредственно нарисованы, а не названы буквами) и т. д.

Цель этих упражнений состоит в том, чтобы добиться от учащихся, чтобы они, видя символ 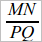(где MN и PQ обозначают отрезки), видели здесь обозначение некоторого, рационального или иррационального, числа.

Все вышеизложенное проведено здесь достаточно подробно потому, что здесь имеется много отличий от обычного изложения. Между тем, казалось бы, что вышеизложенное как раз является естественным развитием возникшего вопроса.

Когда учащиеся привыкнут к измерению одного отрезка другим (или к нахождению их отношения), будут ли считаться данные отрезки соизмеримыми или несоизмеримыми, то явится возможность по поводу одного из таких упражнений (напр., см. прилагаемый чертеж и относящуюся к нему запись) поставить вопрос: итак, нам удалось найти способ измерения одного отрезка другим – какие геометрические знания и какие умения нам для этого необходимы?

 

Всматриваясь во все то, что пришлось здесь делать, можно подметить (и учащиеся при помощи учителя это должны сделать), что мы здесь пользовались: 1) умением откладывать меньший отрезок на большем и связанным с ним знанием, позволяющим отличать равные и неравные отрезки, а в последнем случае больший от меньшего; 2) знанием того, что такое – сумма двух отрезков (в первой же записи имеется AB + KD). То обстоятельство, что иногда приходится писать 2KD (или 3MN и т. п.), не вносят ничего нового, ибо 2KD = KD + KD. Мы видим далее, что иными знаниями или умениями геометрического характера нам здесь не приходится пользоваться, а все дальнейшее сводится лишь к арифметическим расчетам. Поэтому является возможным поставить и такой вопрос: не знаем ли мы в области геометрии каких-либо иных объектов (кроме отрезков), для которых мы обладаем теми же знаниями и умениями? Если мы такие объекты найдем, то мы можем один из них измерять другим. И учащиеся находят такие объекты: 1) углы, 2) площади, 3) дуги одного и того же круга (здесь обычно приходится делать известные указания преподавателю).

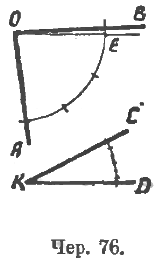
Следует показать, что действительно мы можем любой данный угол AOB измерить другим каким-либо данным углом CKD (принимая ∠CKD за угловую единицу) (чер. 76):

∠AOB = 3∠CKD + ∠BOE;
5∠BOE < ∠CKD < 6∠BOE и т. д.

Затем следует прибавить указания на практически употребляемые угловые единицы (прямой угол, угловой градус, угловая минута и секунда), а также и некоторые упражнения на усвоение этих единиц.

Переходим к дугам одного и того же круга. Здесь, быть может, достаточно лишь общих указаний на возможность измерить одну дугу другою (принимая другую за дуговую единицу) и указаний на практически употребляемые дуговые единицы: дуговые градус, минута и секунда.

Наиболее существенным вопросом здесь является установление связи между измерением дуг круга и углов, имеющих определенное отношение к кругу. На этом останавливаться не буду, так как: 1) в предыдущем уже установлена зависимость между центральными и вписанными углами и 2) в самом вопросе об зависимости между измерением дуг и углов нет моментов, требующих каких-либо особых, кроме обычно выставляемых, соображений.

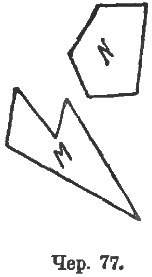
Вопрос об измерении площадей распадается на две части (чер. 77): 1) надо, чтобы учащиеся уяснили себе, что, вообще говоря, всякую площадь (M) можно измерить, принимая другую площадь (N) за единицу площадей (измерить другою площадью N), но что выполнение нужного для этого процесса отложения сопряжено с большой подготовительною работою: нужно предварительно и площадь M и площадь N превратить в площади прямоугольников с одинаковыми, напр., основаниями (в приложении II дано описание этой работы, носящей повторительный характер); 2) надо установить зависимости между измерением площади какой-либо фигуры и измерениями некоторых отрезков, относящихся к этой фигуре.

Что касается прямоугольника, то эта зависимость, выливающаяся в формулу «площадь прямоугольника равна произведению основания на высоту», должна быть выяснена в естественной последовательности: 1) случай, когда при измерении основания и высоты линейною единицею получаются целые числа; 2) случай, когда это измерение дает в результате дробные числа и 3) случай, когда основание и высота (или что-нибудь одно из них) приводят к иррациональным числам.

Подробное рассмотрение этих случаев дано в моей «Геометрии на плоскости». Здесь замечу, что на практике приходится считаться с двумя обстоятельствами: 1) с отсутствием у учащихся ясного представления о действиях (в частности, об умножении) над иррациональными числами и 2) с недостатком времени. Эти обстоятельства часто заставляют, ограничившись рассмотрением 1-го случая и какого-либо простого примера, относящегося ко 2-му случаю, предложить учащимся поверить, что полученная зависимость распространяется и на всевозможные дробные и иррациональные числа.

Переходим к изучению отношений.

Итак, всегда, когда две дроби неравны, можно найти промежуточные для них числа; нельзя этого сделать только тогда, когда данные числа равны. Это свойство и дает нужный нам признак в общей форме:

Если имеем два числа (рацион. или иррац. – безразлично), в какой бы форме они ни были заданы, то эти два числа равны только тогда, когда нельзя найти (рациональных) чисел, больших одного из них и меньших другого.

Если же окажется, что можно найти число, большее первого из данных и меньшее второго, то первое данное число меньше второго.
У нас числа задаются теперь отношениями отрезков; поэтому имеем:

Два отношения равны, если мы убедимся, что нельзя найти какого-либо рационального числа, большего одного из отношений и меньшего другого; если же такое число можно найти и если, например, оно больше 1-го отношения и меньше 2-го, то 1-ое отношение меньше 2-го.

Следующая глава будет рассматривать применение найденного признака, а настоящую закончим указанием, что на практике измеряют один отрезок другим (все равно, соизмеримы ли или нет эти отрезки) при помощи раздела отрезка, принимаемого за линейную единицу, на несколько равных частей и укладывания этой части на измеряемом отрезке точность такого измерения равна той доле линейной единицы, на сколько равных частей она была разделена.