Необходимо, думается, придать этой статье более глубокое, чем это обычно делается, содержание и воспользоваться ею, как хорошим и легким примером для ознакомления учащихся с работою обобщающего мышления.
Для этой цели надо начать с того, что учащиеся должны вспомнить двоякое построение треугольника: 1) можно построить сначала 3 точки, не лежащие на одной прямой, и ими определяется само-собою 3 прямые (можно начать с вершин, определятся стороны); 2) можно начать с построения 3 прямых, не проходящих через одну точку и чтобы между ними не было параллельных, и ими определятся само-собою 3 точки (можно начать со сторон, определятся вершины). Эти 2 построения можно охарактеризовать названиями «треугольник» и «трехсторонник». Теперь желательно каждое из этих построений обобщить: 1) построим сначала 4 точки так, чтобы никакие 3 не лежали бы на одной прямой, – ими определятся прямые; сколько? После выяснения, что их 6 (см. выше при изучении параллелограмма), можно их построить и полученную фигуру назвать полным 4-угольником; 2) построим сначала 4 прямых так, чтобы никакие 3 не проходили бы через одну точку и чтобы среди них не было параллельных, тогда ими определятся их точки пересечения; сколько? После выяснения их числа, можно их отметить и назвать полученную фигуру полным 4-сторонником. Необходимо установить возможность произвести расчет, сколько сторон у полного 4-угольника или сколько вершин у полного 4-сторонника. Например: построено 4 точки, каждую их них можно соединить прямою с любою их трех остальных, т. е. из каждой вершины должны идти 3 прямых; так как всего вершин 4, то их всех вершин должны идти 3 × 4 = 12 прямых, но здесь каждая прямая считается 2 раза (один раз, например, идущею от точки A к точке B, а другой раз – от точки B к точке A). Поэтому всего прямых будет в 2 раза меньше, т. е. 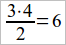 .
.
Далее берем 5 точек, никакие 3 из которых не лежат на одной прямой, рассчитываем, что ими определяется 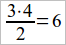 прямых, и получаем полный 5-угольник с 5 вершинами и 10 сторонами. Так же получаем полный 5-сторонник, с 5 сторонами и 10 вершинами.
прямых, и получаем полный 5-угольник с 5 вершинами и 10 сторонами. Так же получаем полный 5-сторонник, с 5 сторонами и 10 вершинами.
Возможно установить и общее положение, что у полного n-угольника имеется n вершин и 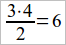 сторон, а у полного n-сторонника – n сторон и
сторон, а у полного n-сторонника – n сторон и 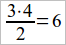 вершин.
вершин.
В виду сложности получаемых фигур возникает желание их упростить, для чего при построении многоугольника возьмем не все определяемые построенными вершинами прямые, а лишь отрезки тех, которые соединяют вершины по порядку. Придется при построении вершин их нумеровать, – получим простые многоугольники (чер. 65).
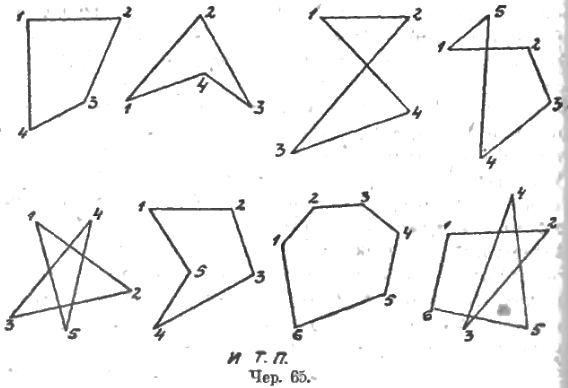
Устанавливается, что каждый простой многоугольник можно рассматривать и как простой многосторонник.
Рассматривая их образы (см. выше, а также целый ряд других), придем к возможности разделить их на 2 разряда. Мы видим, что одни многоугольники выделяют их плоскости определенную часть, которая и является площадью многоугольника (1-ый, 2-ой, 6-ой и 7-ой), а другие вырезают из плоскости несколько кусков (например, 8-ой), так что, если не сделать относительно них каких-либо добавочных условий (основное из этих условий таково: если какой-либо кусок обходится в одном направлении, например, если он остается по левую руку, то он берется для площади со знаком +, а если в противоположном, то – со знаком –), мы не видим, что нам принять за площадь многоугольника. Возможно, в виду этого, в курсе геометрии средней школы ввести названия «многоугольники, имеющие площадь» и «многоугольники, не имеющие площади», причем к последнему следует прибавить указание, что тот, кто умеет разбираться в кусках плоскости, сумеет и для них определить площадь; сразу же ее не видно (к этому разряду относятся многоугольники 3-ий, 4-ый, 5-ый и 8-ой из числа данных на вышеприведенном чертеже).
Рассматривая многоугольники, имеющие площадь, мы прежде всего обращаем внимание на их внутренние углы, понимая под этим те углы, внутри которых лежит или вся площадь многоугольника или, по крайней мере, ее часть (например, угол при вершине 4-ой в многоугольнике 6-м). Отмечаем эти углы и учимся вычислять их сумму, причем удобно вступить на путь индукции: сумма внутренних углов треугольника = 2d; если возьмем 4-угольник, то диагональю он разобьется на 2 треугольника, и сумма внутренних его углов = 2d × 2 = 4d; если возьмем 5-угольник и построим диагонали из одной его вершины, получим 3 треугольника, и сумма его внутренних углов = 2d × 3 = 6d; 6-угольник даст 4 треугольник, 7-угольник – 5 и т. д. и вообще n-угольник даст (n – 2) треугольников и, следовательно, сумма внутренних его углов = 2d(n – 2).
Мы видим еще, что в некоторых многоугольника (имеющих площадь) каждый из внутренних углов меньше выпрямленного (на выше данном чертеже многоугольники 1-ый и 7-ой), а в других имеются внутренние углы, большие выпрямленного (2-ой и 6-ой). Называем первые многоугольники выпуклыми, а вторые – невыпуклыми.
Присоединим еще сюда нахождение суммы внешних углов многоугольника в обычном понимании этого термина и в обычном изложении.
