Из предыдущего мы видим, что основная геометрическая работа есть работа построения и изучения ряда постепенно усложняющихся комбинаций, которые возникают в согласии с известною руководящею мыслью. Раз наше сознание признало существование линий, точек и поверхностей, то «построить известную комбинацию» можно понимать и в том смысле, что наш разум может одновременно мыслить об элементах, составляющих эту комбинацию, или в том, что наше воображение может одновременно представлять элементы, составляющие эту комбинацию. Но этого для выполнения основной работы изучения комбинаций нам недостаточно. Необходимо для нас, по нашей природе, придать этому более материальную форму. И вот вводятся постулаты: мы умеем строить точки, строить прямые линии, строить плоскости, т. е. Мы признаем будто бы возможным осуществлять в материальной форме те элементы геометрии, которые были признаны нами самыми простыми.

Впоследствии к этому мы прибавляем еще необходимый постулат: мы умеем строить круг.

Пусть все эти постулаты – фикция. На самом деле мы не можем получить ни точек, ни прямых, ни плоскостей, ни круга, ибо они не материальны, но эта фикция необходима, без нее мы затрудняемся выполнять работу, какая предстоит при изучении комбинаций, – и эта фикция получает характер законного средства в геометрии.

К словам «мы умеем строить» можно также отнестись различно. Греческая геометрия уже с давних пор (конечно, задолго до Евклида) для осуществления этих постулатов ввела два инструмента, циркуль и линейку, и мы теперь обычно, говоря о построениях, имеем в виду построение при помощи линейки и циркуля. Но для педагогических целей мы можем в известных случаях отнестись к этим словам и иначе, мы можем на помощь призвать и некоторые процессы (например, процесс перегибания; при построении середины отрезка возможно иногда взять этот отрезок на бумажную линейку и перегибанием ее разделить отрезок пополам, а, следовательно, получить его середину) и построение моделей из палочек, дощечек и т. п.

Теперь остановимся на словах «изучить известную комбинацию». Построение определенной комбинации должно явиться следствием какой-либо руководящей мысли, имеющей или форму вопроса или форму достижения известной цели. Тогда может случиться, что уже самый факт построения такой комбинации явится ответом на поставленный вопрос или будет свидетельствовать о возможности или невозможности достижения намеченной цели. Но часто может иметь место случай, что при получении желаемой комбинации становится ясным, что эта комбинация обладает известным свойством; на это свойство (или на эти свойства) нам могут указать или известная симметрия получаемой комбинации или самый процесс, при помощи которого данная комбинация получена. Напомним для примера, что при решении вопроса о дополнении данного угла до выпрямленного удается подметить возможность двоякого решения задачи, откуда становится ясным свойство вертикальных углов.

Конечно, и здесь играет некоторую роль логика: если один угол дополняет данный до выпрямленного, то мы делаем заключение о равенстве этих двух углов. В дальнейшем роль логики усиливается: если новая комбинация – фигура – не обладает какою-либо симметриею, если для получения ее мы не пользовались каким-либо процессом (перегибания, вращения, перемещения и т. п.), а пользовались построением циркулем и линейкою, то это построение позволяет сопоставить вновь полученную комбинацию – фигуру – с изученными ранее. Наблюдательность, отмечающая отдельные моменты построения, укажет, с какими именно уже разученными фигурами следует сопоставить новую, а логика позволит это сопоставление провести так, чтобы не прийти к ложным результатам. Схема этого сопоставления такова: так как мы видим здесь такую-то знакомую фигуру, так как о ней мы знаем такое-то свойство, то для нашей новой фигуры должно иметь место «следующее».

Мы вправе, дабы помочь своему воображению, как-либо иллюстрировать нужные процессы (подобно тому, как мы это постоянно делаем при построении циркулем и линейкою) при помощи предметов. Например, мы можем для иллюстрирования процесса перегибания плоскости взять кусок бумаги и перегибать его в соответствии с условиями, определяющими нужную нам комбинацию. И вот случай, что при такой образной иллюстрации требуемого процесса нам сразу становится ясным непреложность и всеобщая необходимость этого свойства при соответствующих условиях. Здесь имеет место та наша способность, которая носит название «интуиция».

Вопрос, что такое интуиция, не так просто решается, и иногда этим именем называют нечто иное, а именно – простое физическое зрение, а также неуясненный до отчетливости жизненный опыт. Так, при начальном обучении геометрии часто вводят в дело прямой угол, не уяснив его происхождение, и учащихся «на глаз» заставляют определять, получился ли или нет прямой угол. И если учащийся, рассматривая нарисованный квадрат, установит, что у него все углы прямые, то здесь интуиции нет. Здесь имеет место только физическое зрение учащихся и жизненный опыт, хотя бы и маленький, уже приучивший несколько учащихся к тому виду углов, которые в большом числе встречаются в окружающей обстановке – ведь плотники, столяры и т. д. стремятся в своих работах использовать прямые углы. Интуиция здесь могла бы иметь место лишь тогда, когда был бы, с одной стороны, выяснен процесс, приведший к образованию понятия о прямом угле, а с другой стороны, для получения квадрата был бы придуман процесс (или построение), который так осветил бы вопрос об углах квадрата, что сделалась бы сразу ясной неизбежность того, что всегда (а не только у того квадрата, который мы видим нарисованным, либо, как грань деревянного куба) углы квадрата должны быть прямыми. Наилучшее пояснение понятия «интуиция» дает арифметика: из образного представления умножения чисел 4 и 3 (см. прилагаемый чертеж) нам ясно не только то, что 4 × 3 = 3 × 4, но и что подобную же группу предметов мы можем составить для любых двух чисел, и ясна непреложность переместительного закона умножения (ab = ba).

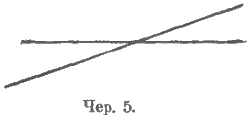
На границе между физическим зрением и интуициею стоит свойство: две прямые пересекаются лишь в одной точке (чер. 5); всякий чертеж пересекающихся прямых дает, в сущности, возможность видеть много общих точек у нарисованных прямых, но нам ясно, что должно считать лишь одну общую точку.

Бывают, однако, случаи, когда физическое зрение как бы заменяет интуицию. Так, объем треугольной призмы должно рассматривать, как сумму объектов трех треугольных пирамид, полученных при помощи определенных сечений; площадь параллелограмма равна площади прямоугольника, получаемого от перенесения части этой площади с одной стороны на другую и т. п.

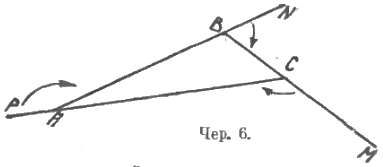
Так как во многих случаях, чтобы вызвать деятельность интуиции, нам приходится пользоваться образным воспроизведением какого-либо процесса, то это обстоятельство дает повод смешивать интуицию с опытом. Опыт может дать толчок для деятельности интуиции, но интуиция отнюдь не сводится только к опыту. Если, например, выполнить опыт сложения трех внутренних углов треугольника, начерченного на бумаге, либо вырезанного из бумаги (в учебниках «наглядных» геометрий часто рекомендуют это делать), то здесь имеет место опыт, и этот опыт отнюдь не покажет обязательность того, чтобы сумма углов треугольника равнялась двум прямым углам или выпрямленному углу. Этот опыт может лишь показать, что для данного (физического) треугольника сумма углов близка к выпрямленному углу; этот опыт может дать лишь толчок для более внимательного рассмотрения вопроса об углах треугольника, и если бы удалось изыскать такой процесс образования треугольника, чтобы из него сделалась ясна неизбежность свойства, что сумма внутренних углов треугольника равна выпрямленному углу, мы тогда пришли бы к открытию этого свойства при помощи интуиции. По-видимому, однако, изыскать такой процесс и дать соответствующее образное воспроизведение этого процесса крайне трудно, а может быть, невозможно; здесь неизбежно, по-видимому, значительное участие логики. Если, например, пользоваться вращением (чер. 6) (прямая AN как бы ломается в точке B и около этой точки вращается – угол поворота отмечен стрелкою, – после чего прямая займет положение BM; затем как бы ломается в точке C и, вращаясь около точки C, приходит в положение CP, после чего этой прямой надо еще повернуться на некоторый угол около точки A, чтобы прийти к начальному положению), то можно добиться без каких-либо заметных логических суждений, что, в общем, прямая сделала полный оборот и, следовательно, повернулась на угол, равный двум выпрямленным. Отсюда при малом участии логики следует, что сумма внешних углов треугольника равна двум выпрямленным углам (или 4 прямым углам), и при несколько большем участии логик явится возможность установить, что сумма внутренних углов треугольника равна одному выпрямленному углу (или 2d).

Так же точно, если мы хотим проиллюстрировать процесс сложения углов треугольника перегибанием вырезанного из бумаги треугольника сначала по средней лини MN (чер. 7) (здесь M есть середина стороны AB и N – середина BC), а затем перегибаниями по MM' (MM' ⊥ AC) и NN' (NN' ⊥ AC), то здесь приходится призвать на помощь логику в следующих пунктах:

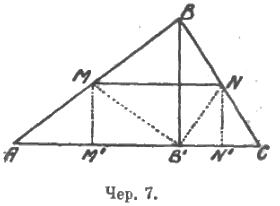
1) ясно, что при перегибании по MN фигура MBN займет положение MB'N, симметричное с прежним относительно оси MN, но как увидеть, не прибегая к помощи логических рассуждений, что точка B' попадает на прямую AC (другими словами: правда ли, что высота треугольника BB' делится прямою MN пополам?

2) При перегибании по MM' (а также по NN') станет ясным, что ∆AMM' займет положение ∆B'MM' только тогда, если мы сошлемся на некоторые свойства равнобедренного треугольника, (что ∆AMB' равнобедренный – это, в сущности, также познается при некотором участии логики: MB' все равно, что MB, а AM = MB, следовательно, и MB' = AM).

Все предыдущие соображения приводят к мысли, что во всякой интуиции должны иметь место, хотя бы минимальное, следы логики. А это обстоятельство, указывает на то, что логика и интуиция настолько тесно переплетаются между собою, что, пожалуй, придется признать задачу «разделить интуицию и логику» невыполнимою.

Даже в аксиомах D. Hilbert'а мы можем видеть это переплетение интуиции и логики. Например, аксиома I₆ говорит: если две точки A и B прямой a лежат на плоскости α, то каждая точка прямой a лежит на плоскости α. После чего следует добавление: в этом случае говорят, что «прямая a лежит на плоскости α». Здесь мы можем видеть и нечто, взятое из образа обычной прямой, лежащей на плоскости; здесь можно подметить и в минимальном ее проявлении и логику: так как прямая здесь рассматривается как комплекс всех ее точек, и так как этом случае все точки этой прямой лежат на плоскости, то следует считать, что и прямая лежит на плоскости. Прибавим сюда слова М. Симона: геометрия есть химическое сочетание наглядного представления и логики. (М. Симон. – «Дидактика и методика математики в средней школе». Сиб. 1912. Стран. 158.)

Резюмируя предыдущее, мы можем установить в следующей форме значение тех средств, при помощи которых развивается содержание геометрии.

Опыт и наблюдение явились тем первоисточником, откуда началась геометрия.

Опыт может побудить предпринять ряд изысканий для того, чтобы увидеть необходимость какого-либо геометрического свойства, либо, наоборот, отвергнуть предполагаемое свойство. Опыт, другими словами, может послужить толчком для начала определенной геометрической работы.

Интуиция и логика, переплетаясь между собою, являются теми орудиями, при помощи которых достигается накопление геометрических знаний. Применение этих орудий совершается или при рассмотрении того процесса, помощью которого получена соответствующая определенному вопросу комбинация, или при сопоставлении новой комбинации, подлежащей разучиванию, с прежними, уже разученными.