При рассмотрении каждого вопроса встречаются количества постоянные и переменные.

Постоянные количества. Количества, не изменяющие своей величины при рассмотрении какого-нибудь вопроса, называются постоянными.

Переменные количества. Количества, могущие изменить свою величину, называются переменными.

Если дан круг, то радиус этого круга величина постоянная, хорды же круга, проходящие через какую-нибудь точку, лежащую на окружности, являются величинами переменными.

Точно также с увеличением числа сторон правильного описанного многоугольника апофемы их остаются величинами постоянными, а периметры величинами переменными.

Переменные величины изменяются в каких-нибудь пределах.

Приближающаяся величина. Когда переменная величина при своем изменении увеличиваясь или уменьшаясь приближается к некоторой постоянной величине так, что разность между ней и постоянной величиной может быть сделана менее всякой данной величины, ее называют величиной приближающейся.

Постоянная величина, к которой приближается переменная величина, называется ее пределом.

Предел. Пределом называется такая постоянная величина, к которой приближается другая переменная величина увеличиваясь или уменьшаясь, но никогда ее не достигая, хотя разность может быть сделана менее всякой данной величины.

Метод пределов. Совокупность свойств, которыми обладают величины приближающиеся и их пределы, и применение этих свойств к решению различных вопросов называют методом пределов.

Из самого определения предела вытекают следующие свойства предела:

1. Предел есть величина постоянная.

2. Приближающаяся величина всегда более или менее предела.

3. Разность между приближающейся величиной и ее пределом может быть сделана меньше всякой данной величины.

Сумма углов правильного многоугольника, имеющего n сторон, выражается формулой:

S = 2d (n - 2) = 2nd - 4d

Величина каждого угла будет

A = S/n = 2d - (4d)/n

Эта величина A есть величина переменная. Она изменяется с увеличением n числа сторон правильного многоугольника.

В этом выражении количество 2d обладает всеми тремя свойствами предела:

1. Во первых количество 2d есть величина постоянная.

2. Во вторых приближающаяся величина A всегда меньше 2d и

3. наконец разность (4d)/n с увеличением n может быть сделана менее всякой данной величины.

С увеличением числа сторон правильного многоугольника величина его каждого угла A, увеличиваясь все более и более, приближается к двум прямым, а два прямых есть предел, к которому стремится эта величина.

Если в уравнении X = K + α количество α может быть сделано менее всякой данной величины, а K есть величина постоянная, то X есть величина приближающаяся, а K есть ее предел.

Предел обозначают словом lim. (limite) или пред. (предел), поставленными перед величиной приближающейся.

Таким образом пишут

K = lim X = lim (K + α)

Из этого соотношения видно, что

lim α = 0.

Бесконечно-малая величина есть величина переменная, имеющая своим пределом нуль.

В методе пределов имеют значение следующие теоремы.

Теорема 129. Если две приближающиеся величины равны, то и пределы их равны.

Дано. Пусть X и Y две приближающиеся величины, A и B их пределы, так что

X = A + α, Y = B + β

Переменные величины α и β могут быть сделаны менее всякой данной величины.

Доказательство. Из того, что две приближающиеся величины X и Y равны, вытекает равенство X = Y или

A + α = B + β (a)

Здесь могут иметь место следующие три предположения:

A > B, A < B и A = B

1. Если бы имело место неравенство A > B, то разность A - B была бы равна некоторой конечной постоянной величине k.

A - B = k = β - α

Так как β и α могут беспредельно уменьшаться, то никак нельзя допустить, чтобы разность β - α равнялась постоянной конечной величине k, следовательно, неравенство A > B невозможно.

2. Точно также неравенство A < B ведет к разности

B - A = l

где l постоянная конечная величина.

Из равенства (a) вытекает равенство

B - A = α - β = l

Это неравенство точно также невозможно, следовательно, невозможно и предположение A < B.

Итак остается справедливым только равенство: A = B (ЧТД).

Теорема 130. Отношение величин приближающихся равно отношению их пределов.

Даны две приближающиеся величины

X = A + α и Y = B + β

Требуется доказать, что X/Y = A/B.

Доказательство. Отношение двух приближающихся величин будет

X/Y = (A + α) / (B + β)

Обозначим конечную величину этого отношения через l, тогда

(A + α) / (B + β) = l

откуда

A + α = Bl + Bβ (1)

A + α есть приближающаяся величина, имеющая своим пределом A; Bl + Bβ есть приближающаяся величина, имеющая своим пределом величину Bl.

На основании предыдущей теоремы равенство (1) ведет к равенству

A = Bl

Следовательно, l = A/B откуда

(A + α) / (B + β) = A/B (ЧТД).

Теорема 131. Внешняя ломаная больше выпуклой кривой, находящейся внутри ломаной.

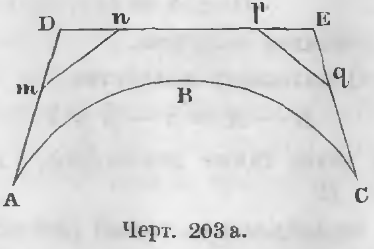
Доказательство. Если бы кривая ABC не была меньше всякой внешней ломаной (черт. 203 а), то существовала бы такая внешняя ломаная, которая была бы меньше всякой другой внешней ломаной, а следовательно и меньше кривой ABC.

Пусть ADEC будет такая ломаная.

В этом случае можно всегда провести так отрезки mn, pq, чтобы они не пересекали кривой ABC, тогда образуется новая ломаная AmnpqC, которая меньше ADEC, ибо

mn < mD + Dn
pq < pE + Eq

Прибавив к этим неравенствам величины Am, np, qC, получим:

mn + pq + Am + np + qC < mD + Dn + pE + Eq + Am + np + qC
или AmnpqC < ADEC.

Таким образом предположение, что существует внешняя ломаная меньше кривой, не имеет места.

Отсюда вытекает следствие: периметр описанного многоугольника больше окружности.

Теорема 132. Разность между периметром одноименного описанного и вписанного многоугольника при удвоении числа сторон может быть сделана меньше всякой данной величины.

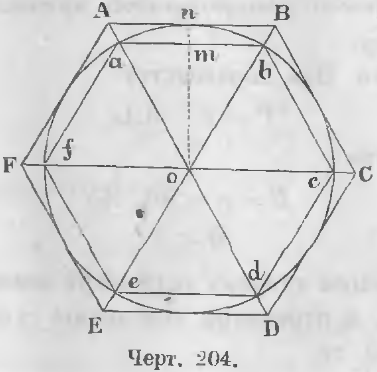
Обозначив через P и p периметры описанного и вписанного многоугольника, имеющего n сторон (черт. 204), мы знаем, что

P/p = OA/Oa

откуда

(P - p)/p = (OA - Oa)/Oa, (P - p)/p = Aa/Oa, P - p = (Aa/Oa)p (a)

Периметр всякого многоугольника больше периметра многоугольника, заключающегося внутри, следовательно, периметр p меньше периметра описанного квадрата.

Периметр описанного квадрата равен 8 · Oa (8 радиусам), следовательно, p < 8 · Oa.

Вставив вместо p во вторую часть равенства (a) величину 8 · Oa, мы ее увеличим, следовательно,

P - p < 8 · Oa · (Aa/Oa) или
P - p < 8Aa

При удвоении числа сторон длина отрезка Aa может быть сделана меньше всякой данной величины, ибо с удвоением числа сторон угол AOB, а следовательно, и угол AOn уменьшаются, и наклонная AO приближается к перпендикуляру nO так, что разность между косвенной и перпендикуляром может быть сделана меньше всякой данной величины.

Теорема 133. С увеличением числа сторон периметры описанного и вписанного многоугольников приближаются к одному и тому же пределу.

Доказательство. Из неравенства

P - p < 8Aa

вытекает равенство

P - p = 8g · Aa

где g < 1.

С удвоением числа сторон периметр описанного многоугольника уменьшается, а периметр вписанного увеличивается. Так как предел Aa равен 0, то предел (P - p) = 0. Откуда пред. P = пред. p, или lim P = lim p (ЧТД).

Теорема 134. Окружность есть предел периметров многоугольников вписанных и описанных.

При удвоении числа сторон периметр правильного описанного многоугольника уменьшается, а периметр вписанного увеличивается. При этом периметр описанного многоугольника больше, а вписанного меньше окружности. Так как разность между периметрами описанного и вписанного многоугольников может быть сделана меньше всякой данной величины, то и подавно с постепенным удвоением числа сторон разность между периметрами правильных многоугольников описанных и окружностью, а также между окружностью и периметрами вписанных правильных многоугольников может быть сделана меньше всякой данной величины, следовательно:

Окружность есть предел периметров вписанных и описанных многоугольников.

Теорема 135. Окружности пропорциональны радиусам.

Доказательство. Обозначим длины двух окружностей через O и O', их радиусы через R и R'.

Впишем в обе окружности правильные многоугольники, имеющие n сторон. Обозначив их периметры через P_n и P_n', мы имеем равенство

P_n/P_n' = R/R'

Так как

P_n = O - α
P_n' = O - β

то предыдущее равенство дает

(O - α)/(O - β) = R/R'

С последовательным увеличением числа сторон разности α и β между окружностями и периметрами вписанных многоугольников могут быть сделаны меньше всякой данной величины, следовательно, разности O - α, O' - β являются величинами приближающимися, а величины O и O' их пределы. На основании теоремы 130 имеем равенство (O - α)/(O' - β) = O/O', откуда

O/O' = R/R'

На основании равенств

O/R = O'/R' или O/2R = O'/2R'

вытекает следствие: отношение каждой окружности к своему диаметру есть величина постоянная.

Это постоянное отношение окружности к диаметру называют буквой π.

Из равенства

O/2R = π

вытекает равенство

O = 2πR

Длина окружности равна радиусу, умноженному на 2π.

Здесь длина выражается в тех же единицах, в каких выражается радиус.

Отвлеченное количество π есть величина несоизмеримая.

Приближенная величина его 22/7 дана Архимедом. Она выражает истинную величину π с точностью до 0,01.

Меций, живший в конце 16-го столетия, нашел для π приближенную величину 355/113 = 3,141592 с точностью до 0,000001.

Это отношение легко помнить, если его представить в виде

1/π = 113 ÷ 355.

Длина дуги, имеющей n градусов. Окружность имеет 360°. Длина окружности радиуса R выражается формулой 2πR. Длина одного градуса будет величина (2πR)/360.

Обозначив через s длину дуги, имеющей n градусов, имеем:

s = (2πRn)/360 (a)

Формула (a) связывает три величины: n число градусов дуги, s ее длину и R радиус круга. Она дает возможность определить одну из них по двум другим.

Определение величины π

Формула, выражающая длину окружности,

O = 2πR

принимает для R = 1 вид

O = 2π

откуда видно, что 2π выражает длину окружности, описанной радиусом равным единице.

Для определения π вычисляют периметры правильных многоугольников вписанного и описанного с одинаковым числом сторон. Длина окружности заключается между периметрами этих многоугольников. Она меньше периметров описанных и больше периметров вписанных многоугольников. Разность между периметрами укажет в каких пределах заключается погрешность в определении окружности, а следовательно и в определении π.

Чтобы убавить эту погрешность в определении π, последовательно вычисляют периметры многоугольников с удвоенным числом сторон.

Разность между периметрами их будет все меньше и меньше, а следовательно, увеличивается и точность, с какой можно определить π.

Обозначив длину стороны правильных многоугольников, имеющих n сторон, вписанного через a_n, описанного через A_n и радиуса через r, мы для определения длины стороны вписанного многоугольника с удвоенным числом сторон пользуется формулой:

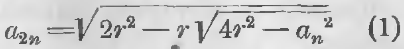
а для определения стороны описанного многоугольника по стороне вписанного формулой:

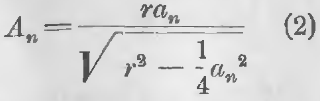
Обозначив через P_n и p_n периметры описанного и вписанного правильного многоугольника, имеем:

P_n = nA_n, p_n = na_n

Приближенная величина π удовлетворяет неравенствам:

π > (na_n)/2, π < (nA_n)/2

в которых a_n и A_n вычислены для окружности с радиусом равным 1, следовательно, в формулах, их определяющих принимают r = 1.

Формулы (1) и (2) для r = 1 принимают вид:

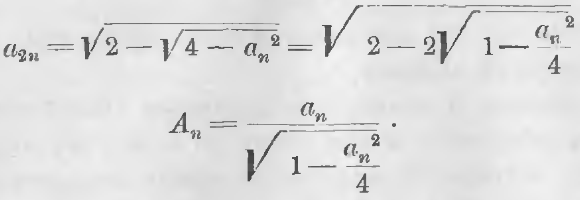
Предположив, что n = 6, мы для a₆ стороны правильного вписанного шестиугольника при r = 1 имеем:

a₆ = 1

откуда

Умножая эти величины на число сторон, имеем следующую таблицу периметров правильных вписанных и описанных многоугольников соответствующего числа сторон, вычисленных с точностью до 6 десятичных знаков

Из этой таблицы видно, что разность между периметрами правильных многоугольников вписанного и описанного все уменьшается.

Для 96-угольника она уже меньше 0,01, а для многоугольника, имеющего 3072 стороны, она меньше 0,00001.

Архимед остановился на вычислении стороны 96-угольника и дал приближенную величину π с точностью до 0,01. Меций дал для π величину π = 355/113 = 3,1415920 с точностью до 0,000001.