Определение параллельных прямых. Параллельными называются две прямые линии, лежащие в одной плоскости и не пересекающиеся на всем своем протяжении.

Прямые AB и CD (черт. 57) будут параллельными. То обстоятельство, что они параллельны, выражают иногда письменно: AB || CD.

Теорема 34. Две прямые, перпендикулярные к одной и той же третьей, параллельны.

Даны прямые CD и EF перпендикулярные к AB (черт. 58)

CD ⊥ AB и EF ⊥ AB.

Требуется доказать, что CD || EF.

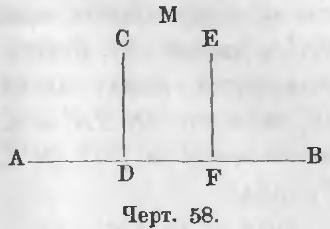
Доказательство. Если бы прямые CD и EF не были параллельны, они пересеклись бы в какой нибудь точке M. В этом случае из точки M на прямую AB были бы опущены два перпендикуляра, что невозможно (теорема 11), следовательно прямая CD || EF (ЧТД).

Теорема 35. Две прямые, из которых одна перпендикулярна, а другая наклонна к третьей, всегда пересекаются.

Даны две прямые EF и CG, из которых EF ⊥ AB, а CG наклонна к AB (черт. 59).

Требуется доказать, что CG встретится с линией EF или что CG не параллельна EF.

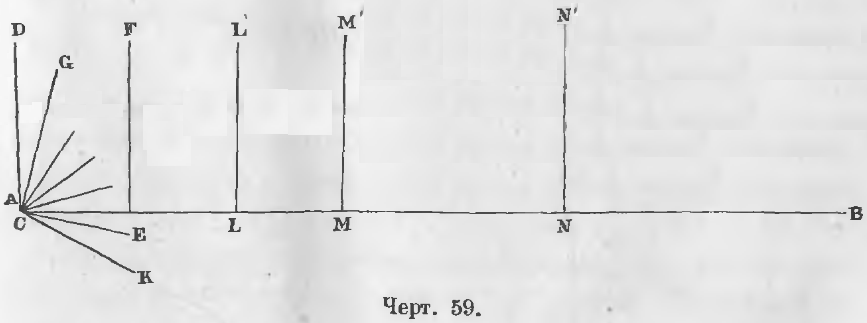
Доказательство. Из точки C восставим к линии AB перпендикуляр CD, тогда при точке C образуется угол DCG, который станем повторять столько раз, чтобы линия CK упала ниже линии AB. Положим, что мы для этого угол DCG повторим n раз, как что

DCK = nDCG

Подобным же образом отложим на прямой AB прямую CE тоже n раз так что CN = nCE.

Из точек C, E, L, M, N восставим перпендикуляры LL', MM', NN'. Пространство, содержащееся между двумя параллельными отрезками CD, NN' и отрезком CN, будет в n раз больше пространства, заключающегося между двумя перпендикулярами CD, EF и отрезком CE, так что DCNN' = nDCEF.

Пространство, заключающееся в угол DCK, содержит в себе пространство DCNN', следовательно,

DCK > CDNN' или
nDCG > nDCEF, откуда
DCG > DCEF.

Последнее неравенство может иметь место только тогда, когда прямая CG выйдет при своем продолжении из пределов пространства DCEF, т. е. когда прямая CG встретится с прямой EF, следовательно прямая CG не параллельна CF (ЧТД).

Теорема 36. Прямая, перпендикулярная к одной из параллельных, перпендикулярна и к другой.

Даны две параллельные прямые AB и CD и прямая EF перпендикулярная к CD (черт. 60).

AB || CD, EF ⊥ CD

Требуется доказать, что EF ⊥ AB.

Доказательство. Если бы прямая AB была наклонна к EF, то две прямые CD и AB пересеклись бы, ибо CD ⊥ EF и AB наклонна к EF (теорема 35), и прямые AB и CD не были бы параллельны, что противоречило бы данному условию, следовательно, прямая EF перпендикулярна CD (ЧТД).

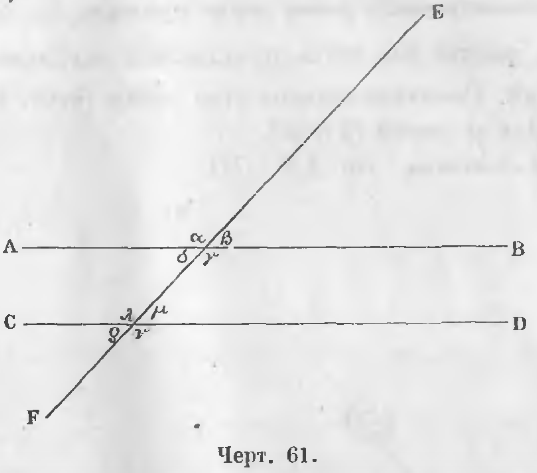
Углы, образуемые пересечением двух прямых третьей прямой. При пересечении двух прямых AB и CD третьей прямой EF (черт. 61) образуется восемь углов α, β, γ, δ, λ, μ, ν, ρ. Эти углы получают особые названия.

1. Четыре угла α, β, ν и ρ называются внешними.

2. Четыре угла γ, δ, λ, μ называются внутренними.

3. Четыре угла β, γ, μ, ν и четыре угла α, δ, λ, ρ называются односторонними, ибо лежат по одну сторону прямой EF.

Кроме того, углы, будучи взяты попарно, получают следующие названия:

4. Углы β и μ называются соответственными. Кроме этой пары такими же соответственными углами будут пары углов: γ и ν, α и λ, δ и ρ.

5. Пары углов δ и μ, а также γ и λ называются внутренними накрест-лежащими.

6. Пары углов β и ρ, а также α и ν называются внешними накрест-лежащими.

7. Пары углов γ и μ, а также δ и λ называются внутренними односторонними.

8. Пары углов β и ν, а также α и ρ называются внешними односторонними.

Условия параллельности двух прямых

Теорема 37. Две прямые параллельны, если при пересечении их третьей у них равны: 1) соответственные углы, 2) внутренние накрест-лежащие, 3) внешние накрест-лежащие, и, наконец, если 4) сумма внутренних односторонних равна двум прямым, 5) сумма внешних односторонних равна двум прямым.

Докажем каждую из этих частей теоремы отдельно.

1-й случай. Соответственные углы равны (черт. 62).

Дано. Углы β и μ равны.

Требуется доказать, что AB || CD.

Доказательство. Если бы линии AB и CD пересекались в точке Q, то получился бы треугольник GQH, у которого внешний угол β равнялся бы внутреннему углу μ, что противоречило бы теореме 22, следовательно, прямые AB и CD не пересекаются или AB || CD (ЧТД).

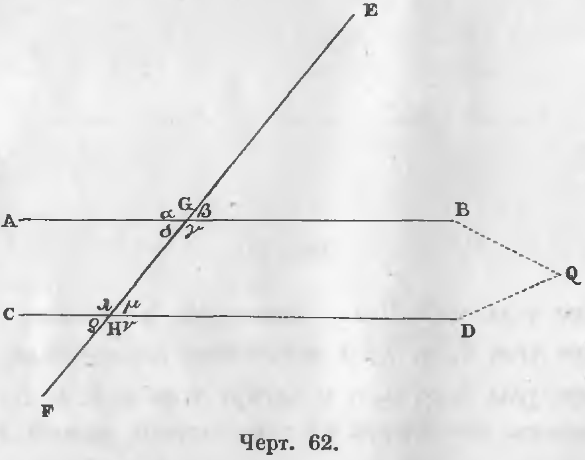
2-й случай. Внутренние накрест-лежащие углы равны, то есть δ = μ.

Доказательство. δ = β как вертикальные, δ = μ по условию, следовательно, β = μ. То есть соответственные углы равны, а в этом случае линии параллельны (1-й случай).

3-й случай. Внешние накрест-лежащие углы равны, то есть β = ρ.

Доказательство. β = ρ по условию, μ = ρ как вертикальные, следовательно, β = μ, т. к. соответственные углы равны. Отсюда следует, что AB || CD (1-й случай).

4-й случай. Сумма внутренних односторонних равна двум прямым или γ + μ = 2d.

Доказательство. β + γ = 2d как сумма смежных, γ + μ = 2d по условию. Следовательно, β + γ = γ + μ, откуда β = μ. Соответственные углы равны, следовательно, AB || CD.

5-й случай. Сумма внешних односторонних равна двум прямым, то есть β + ν = 2d.

Доказательство. μ + ν = 2d как сумма смежных, β + ν = 2d по условию. Следовательно, μ + ν = β + ν, откуда μ = β. Соответственные углы равны, следовательно, AB || CD.

Таким образом, во всех случаях AB || CD (ЧТД).

Теорема 38 (обратная 37). Если две прямые параллельны, то при пересечении их третьей прямой будут равны: 1) внутренние накрест-лежащие углы, 2) внешние накрест-лежащие, 3) соответственные углы и равны двум прямым 4) сумма внутренних односторонних и 5) сумма внешних односторонних углов.

Даны две параллельные прямые AB и CD, то есть AB || CD (черт. 63).

Требуется доказать, что все вышеописанные условия выполняются.

1-й случай. Пересечем две параллельные прямые AB и CD третьей наклонной прямой EF. Обозначим через G и Н точки пересечения прямых AB и CD прямой EF. Из точки O середины прямой GH опустим перпендикуляр на прямую CD и продолжим его до пересечения с прямой AB в точке P. Прямая OQ перпендикулярная к CD перпендикулярна и к AB (теорема 36). Прямоугольные треугольника OPG и OHQ равны, ибо OG = OH по построению, ∠HOQ = ∠POG как вертикальные углы, следовательно, OP = OQ.

 

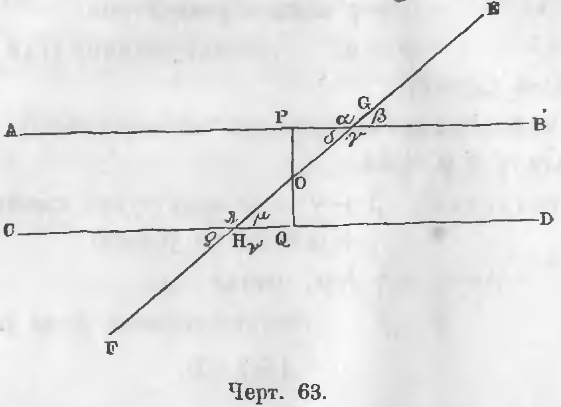
Отсюда следует, что δ = μ, т. е. внутренние накрест-лежащие углы равны.

2-й случай. Если AB || CD, то δ = μ, а так как δ = β, и μ = ρ, то β = ρ, т. е. внешние накрест-лежащие углы равны.

3-й случай. Если AB || CD, то δ = μ, а так как δ = β, то и β = μ, следовательно, соответственные углы равны.

4-й случай. Если AB || CD, то δ = μ, а так как δ + γ = 2d, то и μ + γ = 2d, т. е. сумма внутренних односторонних равна двум прямым.

5-й случай. Если AB || CD, то δ = μ.

Так как μ + ν = 2d, μ = δ = β, следовательно, ν + β = 2d, т. е. сумма внешних односторонних равна двум прямым.

Из этих теорем вытекает следствие. Через точку можно провести только одну прямую, параллельную другой прямой.

Теорема 39. Две прямые, параллельные третьей, параллельны между собой.

Даны три прямые (черт. 64) AB, CD и EF, из которых AB || EF, CD || EF.

Требуется доказать, что AB || CD.

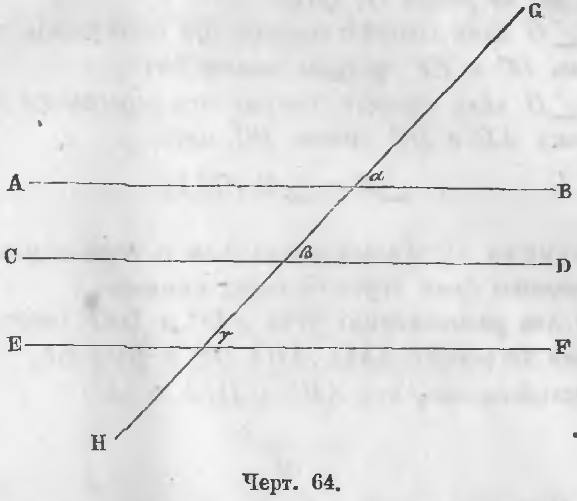
Доказательство. Пересечем эти прямые четвертой прямой GH.

Если AB || EF, то ∠α = ∠γ как соответственные. Если CD || EF, то ∠β = ∠γ также как соответственные. Следовательно, ∠α = ∠β .

Если же соответственные углы равны, то прямые параллельны, следовательно, AB || CD (ЧТД).

Теорема 40. Одноименные углы с параллельными сторонами равны.

Даны одноименные (оба острые или оба тупые) углы ABC и DEF, их стороны параллельны, т. е. AB || DE, BC || EF (черт. 65).

Требуется доказать, что ∠B = ∠E.

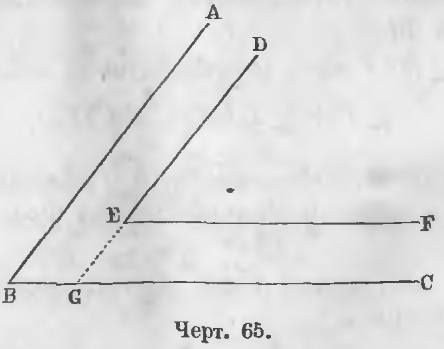
Доказательство. Продолжим сторону DE до пересечения ее с прямой BC в точке G, тогда

∠E = ∠G как соответственные от пересечения сторон параллельных BC и EF третьей прямой DG.

∠B = ∠G как соответственные от пересечения параллельных сторон AB и DG прямой BC, следовательно,

∠E = ∠B (ЧТД).

Теорема 41. Разноименные углы с параллельными сторонами дополняют друг друга до двух прямых.

Даны два разноименные угла ABC и DEF (черт. 66) с параллельными сторонами, следовательно, AB || DE и BC || EF.

Требуется доказать, что ABC + DEF = 2d.

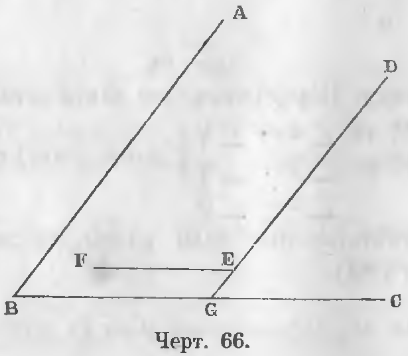
Доказательство. Продолжим прямую DE до пересечения с прямой BC в точке G.

∠B + ∠DGB = 2d как сумма внутренних односторонних углов, образуемых пересечением параллельных AB и DG третьей прямой BC.

∠DGB = ∠DEF как соответственные, следовательно,

∠B + ∠DEF = 2d (ЧТД).

Теорема 42. Одноименные углы с перпендикулярными сторонами равны и разноименные дополняют друг друга до двух прямых.

Рассмотрим два случая: когда А) углы одноименны и когда B) они разноименны.

1-й случай. Стороны двух одноименных углов DEF и ABC (черт. 67) перпендикулярны, т. е. DE ⊥ AB, EF ⊥ BC.

Требуется доказать, что ∠DEF = ∠ABC.

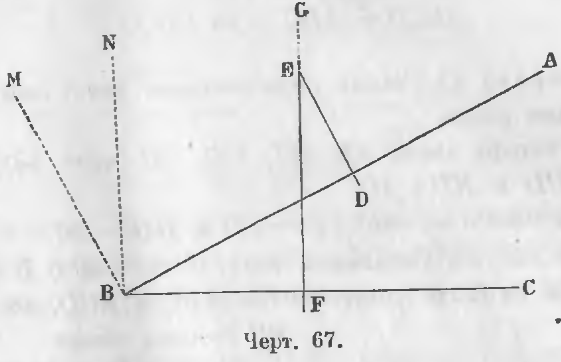
Доказательство. Проведем из точки B прямые BM и BN параллельно прямым DE и EF так, что

BM || DE, BN || EF.

Прямые эти также перпендикулярны к сторонам данного угла ABC, т. е.

BM ⊥ AB и BN ⊥ BC.

Так как ∠NBC = d, ∠MBA = d, то

∠NBC = ∠MBA (a)

Вычтя из обоих частей равенства (а) по углу NBA, находим

∠MBN = ∠ABC

Так как углы MBN и DEF одноименны и с параллельными сторонами, то они равны (теорема 40).

∠MBN = ∠DEF (b)

Из равенств (a) и (b) вытекает равенство

∠ABC = ∠DEF (ЧТД).

2-й случай. Углы GED и ABC с перпендикулярными сторонами разноименны.

Требуется доказать, что ∠GED + ∠ABC = 2d (черт. 67).

Доказательство. Сумма углов GED и DEF равна двум прямым.

GED + DEF = 2d
DEF = ABC, следовательно,
GED + ABC = 2d (ЧТД).

Теорема 43. Части параллельных прямых между другими параллельными равны.

Даны четыре прямые AB, BD, CD, AC (черт. 68), из которых AB || CD и BD || AC.

Требуется доказать, что AB = CD и BD = AC.

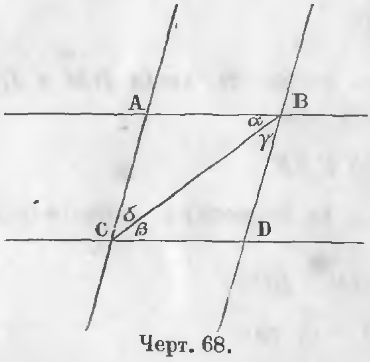
Доказательство. Соединив точку C с точкой B отрезком BC, получим два равных треугольника ABC и BCD, ибо

BC — сторона общая,

∠α = ∠β (как внутренние накрест-лежащие от пересечения параллельных прямых AB и CD третьей прямой BC),

∠γ =∠δ (как внутренние накрест-лежащие от пересечения параллельных прямых BD и AC прямой BC).

Таким образом, треугольники имеют по равной стороне и по двум равным углам, лежащим на ней.

Против равных углов α и β лежат равные стороны AC и BD, и против равных углов γ и δ - равные стороны AB и CD, следовательно,

AC = BD, AB = CD (ЧТД).

Теорема 44. Параллельные прямые на всем своем протяжении находятся на равном расстоянии друг от друга.

Расстояние точки от прямой определяется длиной перпендикуляра, опущенного из точки на прямую. Чтобы определить расстояние каких угодно двух точек A и B параллельной AB от CD, из точек A и B опустим перпендикуляры AC и BD.

Дана прямая AB параллельная CD, отрезки AC и BD перпендикулярны к прямой CD, т. е. AB || CD, AC ⊥ DC, BD ⊥ CD (черт. 69).

Требуется доказать, что AC = BD.

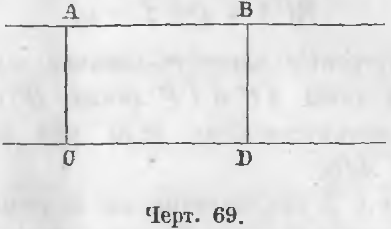
Доказательство. Прямые AC и BD, будучи обе перпендикулярными к CD, параллельны, а следовательно, AC и BD как части параллельных между параллельными, равны, т. е. AC = BD (ЧТД).

Теорема 45 (обратная 43). Если противоположные части четырех пересекающихся прямых равны, то эти части параллельны.

Даны четыре пересекающиеся прямые, противоположные части которых равны: AB = CD и BD = AC (черт. 68).

Требуется доказать, что AB || CD и BD || AC.

Доказательство. Соединим точки B и C прямой BC. Треугольники ABC и BDC равны, ибо

BC — общая сторона,
AB = CD и BD = AC по условию.

Отсюда

∠α = ∠β, ∠γ =∠δ

Следовательно,

AC || BD, AB || CD (ЧТД).

Теорема 46. Сумма углов треугольника равна двум прямым.

Дан треугольник ABC (черт. 70).

Требуется доказать, что A + B + C = 2d.

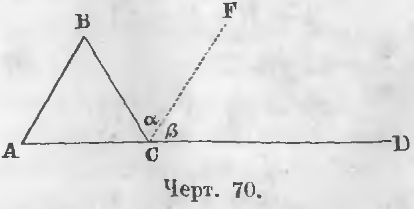
Доказательство. Проведем из точки C прямую CF параллельную стороне AB. При точке C образуется три угла BCA, α и β. Сумма их равна двум прямым:

BCA + α + β = 2d

α = B (как внутренние накрест-лежащие углы при пересечении параллельных прямых AB и CF прямой BC);

β = A (как соответственные углы при пересечении прямых AB и CF прямой AD).

Заменяя углы α и β их величинами, получим:

BCA + A + B = 2d (ЧТД).

Из этой теоремы вытекают следующие следствия:

Следствие 1. Внешний угол треугольника равен сумме внутренних не смежных с ним.

Доказательство. Действительно, из чертежа 70,

∠BCD = ∠α + ∠β

Так как ∠α = ∠B, ∠β = ∠A, то

∠BCD = ∠A + ∠B.

Следствие 2. В прямоугольном треугольнике сумма острых углов равна прямому.

Действительно, в прямоугольном треугольнике (черт. 40)

A + B + C = 2d, A = d, следовательно,
B + C = d.

Следствие 3. В треугольнике не может быть больше одного прямого или одного тупого угла.

Следствие 4. В равностороннем треугольнике каждый угол равен 2/3 d.

Действительно, в равностороннем треугольнике

A + B + C = 2d.

Так как A = B = C, то

3A = 2d, A = 2/3 d.