Теорема 11. Из точки, лежащей вне прямой, на данную прямую можно опустить только один перпендикуляр.

Дана линия AB и внешняя точка C (чер. 29).

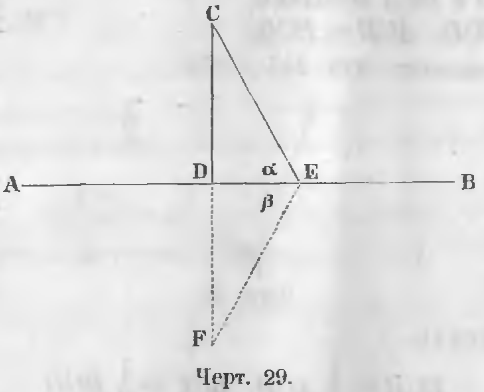
Требуется доказать, что можно опустить только одни перпендикуляр.

Доказательство. Предположим, что из точки C опущены на прямую AB два перпендикуляра CD и CE. Продолжим линию CD и отложим на ней точку F на расстоянии DF равном CD и соединим точку F с E.

Перегнем около линии AB верхнюю часть чертежа, тогда

a) линия CD пойдет по направлению линии DF, ибо углы CDE и EDF равны как прямые.

b) точка C совпадает с точкой F, ибо CD = DF по построению, и

c) линия CE совпадет с линией EF, следовательно, угол α = углу β.

Угол α прямой, следовательно, и угол β тоже прямой.

Сумма углов α + β = 2d, следовательно, по теореме 6, две стороны CE и EF составляют одну прямую CEF. Таким образом между двумя точками C и F проведены две не совпадающие прямые CDF и CEF. Это невозможно, следовательно, из точки C на линию AB дух перпендикуляров провести нельзя.

Кроме перпендикуляра всякая линия CE, идущая от точки C до прямой, называется наклонной или косвенной.

Теорема 12. Перпендикуляр короче наклонной.

Даны перпендикуляр CD и наклонная CE (чер. 29).

Требуется доказать, что CD < CE.

Доказательство. Из предыдущего построения видно, что

CE = EF.

Прямая менее ломаной, следовательно,

CD + DF < CE + EF.

Так как CE = EF, CD = DF, то

2CD < 2CE, откуда CD < CE (ЧТД).

Расстояние DE называется расстоянием наклонной от перпендикуляра. Это расстояние есть расстояние подошвы перпендикуляра от подошвы наклонной.

Так как перпендикуляр короче всякой наклонной, то длина его выражает собой кратчайшее расстояние от точки до прямой линии.

Отсюда вытекает следующее заключение. Кратчайшее расстояние точки от прямой равно длине перпендикуляра, опущенного из точки на прямую линию.

Теорема 13. Наклонные, равноотстоящая от перпендикуляра, равны.

Даны линии CD ⊥ AB (чер. 30) и две наклонные DM и DN, находящиеся на равных расстояниях CM и CN (CM = CN).

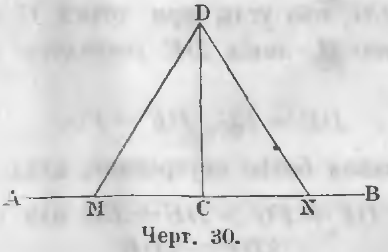
Требуется доказать, что DM = DN.

Доказательство. Повернем левую часть чертежа около линии CD, как около оси, тогда a) линия CA пойдет по линии CB, ибо углы при C прямые, b) точка M совпадет с N, ибо CM = CN по условию, и линия DM совпадет с линией DN всеми своими точками, следовательно

DM = DN (ЧТД).

Теорема 14. На большем расстоянии от перпендикуляра находится большая наклонная.

Даны DC ⊥ AB и две наклонные DF и DE, находящиеся на расстоянии CF и CE, из которых CF > CE (чер. 31).

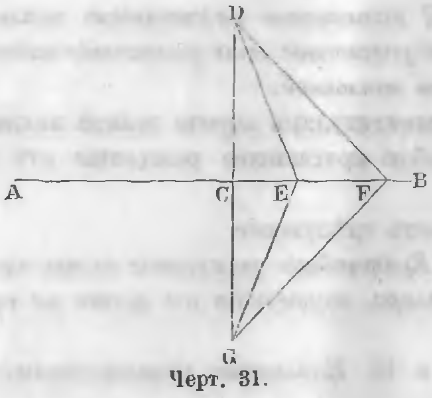
Требуется доказать, что DF > DE.

Доказательство. a) Продолжим линию DC и отложим линию CG = CD.

Соединим точки E и F с точкой G. Повернув верхнюю часть чертежа около линии AB, как около ос, увидим, что линия DC пойдет по линии CG, ибо углы при точке C прямые, точка D совпадет с точкою G, линия DE совпадет с линией EG, а DF с FG, следовательно,

DE = EG, DF = FG.

b) Внешняя ломаная больше внутренней, следовательно,

DF + FG > DE + EG или 2DF > 2DE

Сократив на 2, имеем:

DF > DE (ЧТД).

Теорема 15 (обратная 14). Большая наклонная более удалена от перпендикуляра.

Даны DC ⊥ AB и две наклонные DF и DE, из которых DF > DE (чер. 32).

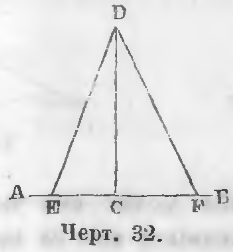
Требуется доказать, что CF > CE.

Доказательство. Тут могут быть три случая: CF > CE, CF = CE и CF < CE.

a) Если бы линия CF была меньше CE, то по теореме 14 линия DF тоже была бы < DE, что противоречит условию.

b) Если бы CF = CE, по теореме 13 было бы DF = DE, что также противоречит условию, следовательно, CF > CE (ЧТД).

Теорема 16 (обратная 13). Равные наклонные находятся на равном расстоянии от перпендикуляра.

Даны равные наклонные DM и DN (черт. 30) (DM = DN).

Требуется доказать, что CN = CM.

Доказательство. Здесь могут быть три случая: CN > CM, CN < CM, CN = CM.

a) Если бы было CN > CM, по теореме 14 было бы DN > DM, что противоречит условию.

b) Если бы было CN < CM, то было бы и DN < DM, что также противоречит данному условию, следовательно CN = CM (ЧТД).

Теорема 17. Каждая точка перпендикуляра, восставленного из середины отрезка, находится на равных расстояниях от его концов.

Дано. Точка C есть середина отрезка AB, следовательно, AC = CB и линия CD ⊥ AB (черт. 33).

Требуется доказать, что DA = DB.

Доказательство. Наклонные DA и DB, находящиеся на равных расстояниях CA и CB, равны, следовательно, DA = DB (ЧТД).

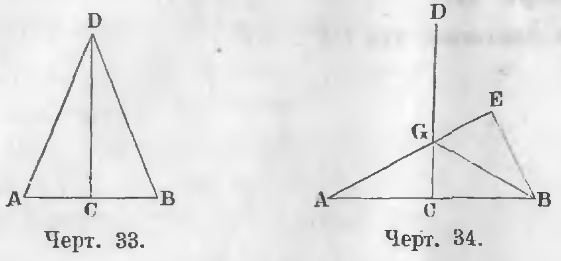
Теорема 18. Все точки вне перпендикуляра не находятся на равных расстояниях от его концов.

Дана точка E вне перпендикуляра CD (чер. 34).

Требуется доказать, что ее расстояния до концов отрезка AB не равны.

Доказательство. Соединим G, точку пересечения линий AE и CD с концом B, тогда AG = GB.

Ломаная EGB больше EB или

BG + GE > EB

Заменив BG равной линией AG (т. 17), имеем:

AG + GE > EB или AE > EB (ЧТД).