Четыре отрезка называются пропорциональными, если они такой величины, что образуют пропорцию. В этом случае отношение двух отрезков по длине равно отношению других двух отрезков.
Так четыре отрезка AB, CD, EF, GH (черт. 144) будут пропорциональными, если они удовлетворяют пропорции:
AB/CD = EF/GH (1).

В этой пропорции под отрезками AB, CD подразумевают их длины. Так как длина отрезков может быть выражена числом, которое выражает отношение длины отрезка к длине, принятой за единицу, то под отрезками AB, CD, EF, GH можно подразумевать и сами числа.
На этом основании пропорция из отрезков обладает всеми свойствами пропорции, составленной из чисел.
Члены пропорции можно переставлять, перемножать и т. д.
Таким образом из пропорции (1) вытекает равенство
а также пропорции:
AB/EF = CD/GH, GH/CD = EF/AB и т. д.
Каждый из отрезков по отношению к остальным называется четвертым пропорциональным.
Таким образом отрезок GH будет четвертым пропорциональным отрезкам EF, CD, AB. Отрезок AB четвертым пропорциональным отрезкам CD, EF, GH.
Теоремы о пропорциональных отрезках
В основу всех предположений о пропорциональных отрезках может быть положена следующая теорема.
Теорема 83. Если от вершины угла по стороне его отложим несколько равных частей и проведем через точки деления параллельные прямые до другой стороны угла, на последней отложатся тоже равные части.
Дан угол ABC (черт. 145), на одной стороне которого отложены равные части BD, DE, EF, FG и проведены параллельные линии DD', EE', FF', GG', то есть
BD = DE = EF = FG
DD' || EE' || FF' || GG'
Требуется доказать, что
BD' = D'E' = E'F' = F'G'.
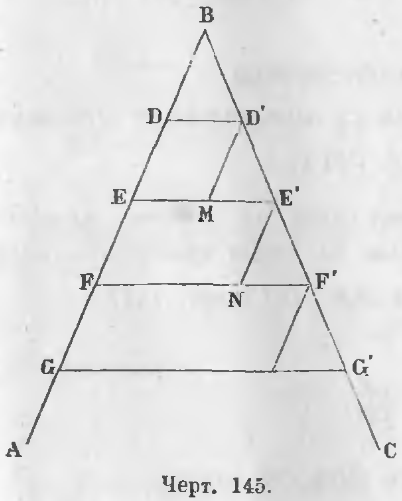
Доказательство. Проведем отрезок D'M параллельно лучу AB. Треугольники BDD' и D'ME' равны, ибо D'M = BD (потому что D'M = DE как части параллельных между параллельными, а DE = BD по условию, следовательно, D'M = BD).
∠B = ∠MD'E' (как соответствующие углы при пересечении параллельных прямых BD и D'M третьей прямой BC).
∠BDD' = ∠D'ME' (ибо ∠BDD' = ∠BEE', а ∠BEE' = ∠D'ME'). Следовательно, BD' = D'E'.
Подобным же образом, проведя отрезок E'N параллельно AB, можно доказать, что D'E' = E'F'. Следовательно,
BD' = D'E' = E'F' = … (ЧТД).
Теорема 84. Если на одной прямой отложим несколько равных частей и проведем параллельные прямые до пересечения с другой прямой, на последней отложатся тоже равные части.
Дано. На прямой AB отложены равные части EF, FG и проведены параллельные прямые EE', FF', GG' (черт. 146).
Требуется доказать, что E'F' = F'G' и т. д.
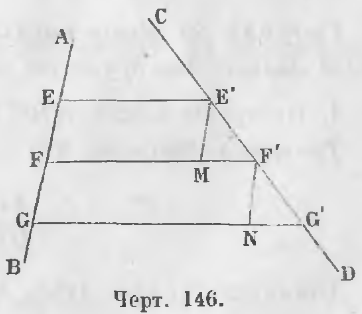
Доказательство. Проведем отрезки E'M, F'N параллельно прямой AB, тогда треугольники E'MF' и F'NG' равны, ибо E'M = F'N (E'M = EF, F'N = FG и так как EF = FG, то E'M = F'N).
∠ME'F' = ∠NF'G' как соответственные.
∠E'MF' = ∠F'NG' как углы с параллельными сторонами.
Следовательно,
E'F' = F'G' (ЧТД).
Теорема 85. Прямая, параллельная одной из сторон треугольника, делит две другие его стороны на части пропорциональные.
Дано. В треугольнике ABC прямая DE || BC (черт. 147).
Требуется доказать, что
AD/DB = AE/EC.
Доказательство. Здесь могут быть два случая:
1) когда отрезки AD и DB соизмеримы и
2) когда они несоизмеримы.
Первый случай. Отрезки AD и DB соизмеримы. Положим, что их общая мера укладывается m раз в отрезке AD и n раз в отрезке DB. Разделив AD на m и DB на n равных частей и проведя из точек деления прямые, параллельные BC, мы разделим также и отрезок AE на m, а EC на n равных частей (теорема 83).
Рядом с отношением
AD/DB = m/n
имеет место отношение
AE/EC = m/n
следовательно,
AD/DB = AE/EC.
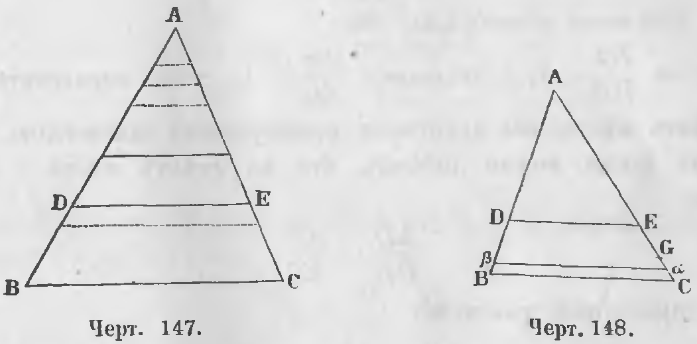
Второй случай. Отрезки AD и DB несоизмеримы (черт. 148).
Докажем, что в этом случае не имеет мета ни неравенство
AD/DB > AE/EC
ни неравенство
AD/DB < AE/EC
a) Допустим, что имеет место неравенство
AD/DB > AE/EC (a).
Чтобы имело место равенство, нужно второе отношение увеличить. Для этого нужно знаменатель этого отношения уменьшить, т. е. EC заменить меньшим отрезком EG. Тогда будет иметь место пропорция
AD/DB = AE/EG (1).
Разделим отрезок AE на равные части, которые были бы меньше GC, и станем их откладывать от точки A по отрезку AC; тогда одна из частей упадет в точку α между G и C. Проведем из точки α прямую αβ параллельную BC, тогда отрезок AE будет соизмерим с Eα и будет иметь место пропорция
AD/Dβ = AE/Eα (2)
Разделив отношение (1) на (2), получим равенство
Dβ/DB = Eα/EG.
Это равенство несообразно, ибо отношение Dβ/DB < 1, а отношение Eα/EG > 1, следовательно, неравенство (a) не имеет места, ибо ведет к несообразному заключению.
Точно также можно доказать, что не имеет места и неравенство
AD/DB < AE/EC
следовательно, справедливо равенство
AD/DB = AE/EC (ЧТД).
Теорема 86. Прямая, параллельная одной из сторон треугольника, отсекает треугольник, стороны которого пропорциональны сторонам целого треугольника.
Дано. Линия DE параллельна BC (черт. 149) DE || BC.
Требуется доказать, что AB/AD = AC/AE = BC/DE.
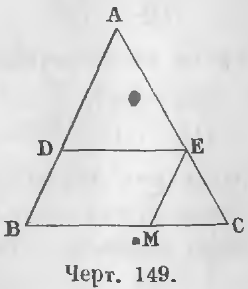
Доказательство. Отрезок DE, параллельный BC, делит по предыдущей теореме стороны AB и AC на части пропорциональные, следовательно,
AD/DB = AE/EC.
По свойству пропорции имеем:
(AD + DB)/DB = (AE + EC)/EC, откуда
AB/DB = AC/EC,
а также
(AD + DB)/AD = (AE + EC)/AE, откуда
AB/AD = AC/AE (a)
Подобным же образом, проведя отрезок EM параллельно AB, имеем:
AC/AE = BC/BM (b)
Так как BM = DE как части параллельных между параллельными, то пропорция (b) обратится в пропорцию
AC/AE = BC/DE (c)
Сопоставляя пропорции (a) и (c), получим три равных отношения:
AB/AD = AC/AE = BC/DE (ЧТД).
Теорема 87 (обратная 86). Прямая, делящая стороны треугольника на части пропорциональные, параллельна третьей стороне.
Дано. В треугольнике ABC отрезок DE (черт. 150) делит его стороны на части пропорциональные, т. е. AB/AD = AC/AE (a).
Требуется доказать, что DE || BC.
Доказательство. Положим, что отрезок DE не параллелен BC.
Проведем из точки D отрезок DF, параллельный BC. По предыдущей теореме
AB/AD = AC/AF (b)
В двух пропорциях (a) и (b) три члена равны, следовательно, и четвертые члены должны быть равны, т. е.
AE = AF,
что несообразно, ибо целое не равно своей части, следовательно, допущение, что отрезок DE не параллелен BC ведет к нелепости. Отсюда заключаем, что DE || BC (ЧТД).
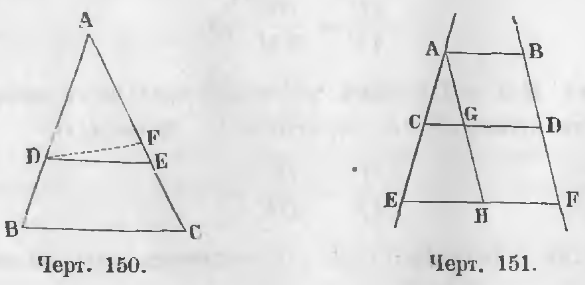
Теорема 88. Три параллельные прямые отрезывают на двух других прямых части пропорциональные.
Даны две прямые AE и BF и три параллельных AB, CD, EF (черт. 151).
Требуется доказать, что AC/CE = BD/DF.
Доказательство. Проведя отрезок AH параллельно BF, имеем треугольник AEH, в котором отрезок CG параллелен EH, следовательно (теорема 85)
AC/CE = AG/GH
Так как
AG = BD, GH = DF, то
AC/CE = BD/DF (ЧТД).
