В двух треугольниках, имеющих равные углы, стороны, лежащие против одинаковых углов, называются сходственными (соответственными).

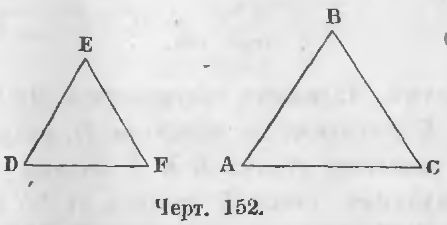
В треугольниках ABC и DEF (черт. 152), в которых

∠A = ∠D, ∠B = ∠E, ∠C = ∠F

стороны AB и DE, BC и EF, AC и DF, лежащие против равных углов C и F, A и D, B и E будут соответственными сторонами.

Определение подобных треугольников. Подобными называются такие два треугольника, у которых углы равны и сходственные стороны пропорциональны.

Если в двух треугольниках (черт. 152) ABC и DEF углы равны

∠A = ∠D, ∠B = ∠E, ∠C = ∠F

и соответственные стороны пропорциональны

AB/DE = AC/DF = BC/EF

то треугольники называются подобными.

Подобие обычно выражают знаком ∼.

Подобие двух треугольников изображают письменно:

ABC ∼ DEF.

Случаи подобия треугольников

Теорема 89. (Первый случай подобия.) Два треугольника подобны, если три угла одного равны трем углам другого треугольника.

Дано. В треугольниках ABC и DEF углы равны (черт. 153).

∠A = ∠D, ∠B = ∠E, ∠C = ∠F

Требуется доказать, что они подобны. Для этого нужно доказать, что их стороны пропорциональны, т. е. удовлетворяют отношениям:

AB/DE = AC/DF = BC/EF

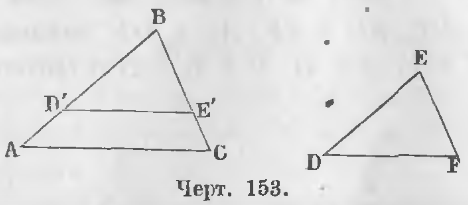
Доказательство. Наложим треугольник DEF на ABC так, чтобы вершина E совпала с вершиной B, сторона ED со стороной AB. По равенству углов B и E сторона EF пойдет по стороне BC. Положим, точка D упадет в D', а точка F в E'. Треугольник D'BE' равен треугольнику DEF, следовательно,

∠D' = ∠D, ∠D = ∠A

откуда

∠D' = ∠A.

Если соответственные углы равны, то D'E || AC.

По теореме 86 имеют место равенства

AC/D'E' = AB/BD' = BC/BE'

Так как BD' = ED, BE' = EF, D'E' = DF, то

AC/DF = AB/ED = BC/EF (ЧТД).

Теорема 90 (второй случай подобия). Два треугольника подобны, если они имеют по два равных угла.

Доказательство. Если в двух треугольниках ABC и DEF два угла равны (черт. 153).

A = D, B = E

то и третьи углы тоже равны, а в таком случае треугольники подобны (теорема 89).

Теорема 91 (третий случай подобия). Два треугольника подобны, если они имеют по равному углу, заключающемуся между пропорциональными сторонами.

Дано. В треугольниках ABC и DEF (черт. 153) углы B и E равны, и стороны, их содержащие, пропорциональны, т. е.

∠B = ∠E и AB/DE = BC/EF.

Требуется доказать, что треугольники подобны.

Доказательство. Совместим угол E с углом B, и отложим BD' = ED, BE' = EF, тогда ∆BD'E' = ∆DEF, следовательно,

∠D' = ∠D, ∠E' = ∠F.

Так как имеет место пропорция

AB/BD' = BC/BE'

то сторона D'E' || AC (теорема 87).

Поэтому ∠D' = ∠A, ∠C = ∠E'.

Следовательно,

∠A = ∠D, ∠C = ∠F, ∠B = ∠E

т. е. три угла одного равны трем углам другого треугольника.

В этом же случае треугольники ABC и DEF подобны (ЧТД).

Теорема 92 (четвертый случай подобия). Два треугольника подобны, если стороны одного пропорциональны сторонам другого.

Дано. В треугольниках ABC и abc (черт. 154) стороны пропорциональны:

AB/ab = BC/bc = AC/ac (1)

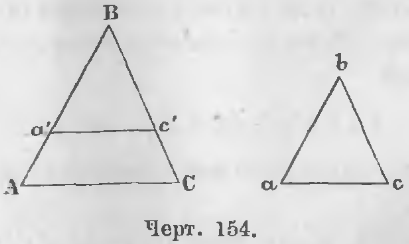
Требуется доказать, что у них углы равны, т. е.

A = a, B = b, C = c.

Доказательство. Отложим на стороне BA отрезок Ba', равный ba, и проведем отрезок a'c', параллельный AC, тогда будут иметь место отношения:

AB/Ba' = BC/Bc' = AC/a'c'

Так как Ba' = ba, то рядом с этими имеют место отношения:

AB/ab = BC/Bc' = AC/a'c' (2)

Сопоставляя отношения (1) и (2), заключаем, что

Bc' = bc, a'c' = ac,

следовательно, два треугольника a'Bc' и abc равны, откуда

∠B = ∠b, ∠Ba'c' = ∠a, ∠Bc'a' = ∠c

а так как

∠A = ∠a', ∠C = ∠c', то
B = b, A = a, C = c,

следовательно, углы двух треугольников ABC и abc равны (ЧТД).

Теорема 93 (пятый случай подобия). Два треугольника подобны, если стороны одного параллельны сторонам другого.

Доказательство. Здесь могут быть два случая:

1-й случай. Если углы двух треугольников с параллельными сторонами обращены в одну сторону. В таком случае в двух таких треугольниках ABC и abc (черт. 155) все углы одного соответственно равны углам другого, и, следовательно, треугольники подобны.

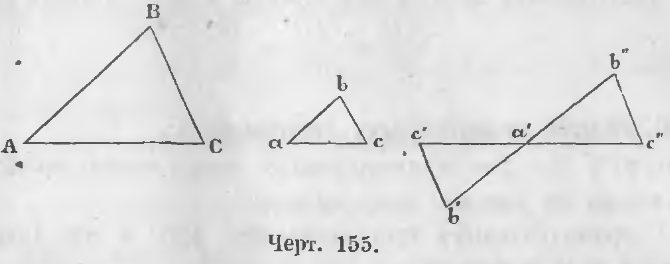
2-й случай. Когда углы с параллельными сторонами обращены в разные стороны. Так в треугольниках ABC и a'b'c' стороны параллельны.

AB || a'b', AC || a'c', BC || b'c'.

Углы же между параллельными сторонами обращены в разные стороны.

В таком случае, продолжив стороны a'c' и a'b', откладываем на продолжении их части a'b'' = a'b' и a'c'' = a'c'.

Треугольники a'b''c'' и a'b'c' равны. Треугольник a'b''c'' подобен треугольнику ABC, ибо у него стороны параллельны и углы, направленные в одну сторону, равны, следовательно,

∆ABC ~ a'b''c'', следовательно, ∆ABC ~ a'b'c' и
AB/a'b' = AC/a'c' = BC/b'c'

Теорема 94 (шестой случай подобия). Два треугольника подобны, если стороны одного перпендикулярны к сторонам другого.

Даны два треугольника ABC и abc (черт. 156), стороны которых перпендикулярны:

ab ⊥ AB, ac ⊥ AC, bc ⊥ BC

Требуется доказать, что треугольники подобны.

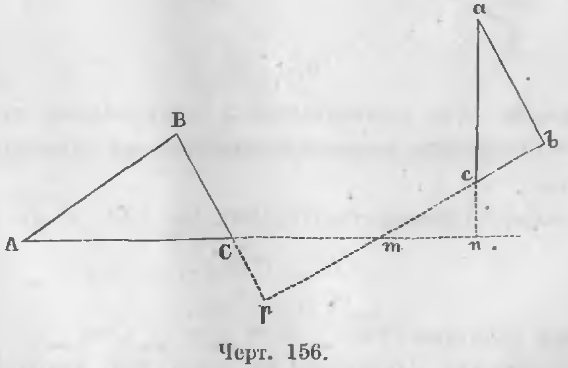
Доказательство. Продолжим стороны ac и bc до пересечения их со сторонами AC и BC в точках n и p. Тогда в двух треугольниках mcn и mCp все углы равны, ибо

n = p как прямые

Углы при точке m равны как вертикальные,

а следовательно, и третьи углы равны ∠pCm = ∠mcn.

Так как

∠pCm = ∠ACB, ∠mcn = ∠acb

следовательно,

∠ACB = ∠acb

Подобным же образом можно доказать, что A = a, B = b, следовательно, треугольники ABC и abc подобны и имеет место пропорция

AB/ab = AC/ac = BC/bc

Подобие прямоугольных треугольников

Теорема 95. Два прямоугольных треугольника подобны, если они имеют по равному острому углу.

Дано. У прямоугольных треугольников ABC и abc (черт. 157) острые углы C и c равны.

Требуется доказать, что треугольники ABC и abc подобны.

Доказательство. Углы B и b равны как прямые, углы C и c равны по условию, следовательно, они подобны (теорема 90).

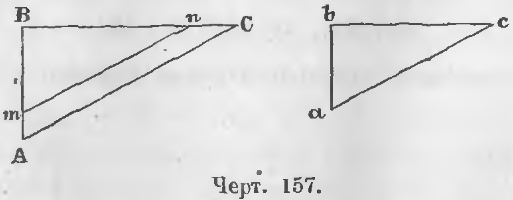
Теорема 96. Два прямоугольных треугольника подобны, если катет и гипотенуза одного пропорциональна катету и гипотенузе другого.

Дано. В прямоугольных треугольниках ABC и abc (черт. 157)

AC/ac = AB/ab (a)

Требуется доказать, что ∠A = ∠a, ∠C = ∠c.

Доказательство. Отложим на отрезке BA отрезок Bm, равный ba и из точки m проведем отрезок mn, параллельный ac, тогда имеет место пропорция:

AC/mn = AB/Bm (b)

Так как Bm = ab по построению, то, сравнивая две пропорции (a) и (b), заключаем, что ac = mn, следовательно, два прямоугольных треугольника Bmn и abc, имея по равному катету и равной гипотенузе, равны.

Действительно, у них Bm = ab, mn = ac. У равных треугольников и углы равны:

∠m = ∠a = ∠A и ∠n = ∠c = ∠C

следовательно, два треугольника ABC и abc подобны.

Теорема 97. В подобных треугольниках высоты пропорциональны сторонам.

Даны два подобных треугольника ABC и FED (черт. 158), следовательно,

∠A = ∠F, ∠B = ∠E, ∠C = ∠D и
AB/FE = BC/ED = AC/DF

и проведены высоты BH и Eh.

Требуется доказать, что AB/FE = BH/Eh.

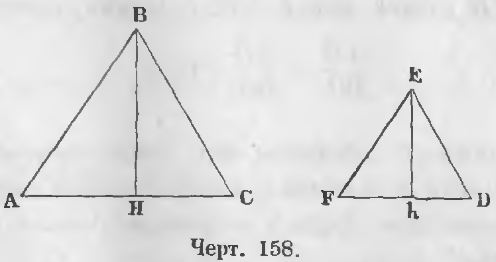
Доказательство. Прямоугольные треугольники ABH и FEh подобны, ибо ∠A = ∠F по условию, ∠AHB = ∠FhE как прямые, следовательно,

AB/FE = BH/Eh (ЧТД).

Теорема 98. Прямая, разделяющая угол треугольника пополам, делит его противоположную сторону на части пропорциональные двум другим сторонам.

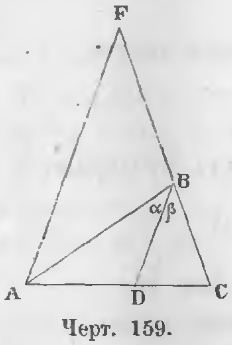
Дано. Отрезок BD делит угол B треугольника ABC пополам (черт. 159).

∠ABD = ∠DBC или ∠α = ∠β

Требуется доказать, что AB/BC = AD/DC.

Доказательство. Проведем из точки A отрезок AF параллельный BD до пересечения его с прямой BC в точке F. В треугольнике FBA

∠AFB = ∠β как соответственные углы,
∠FAB = ∠α как внутренние накрест-лежащие углы от пересечения параллельных AF и BD третьей прямой AB.

Так как ∠α = ∠β по условию, то

∠AFB = ∠FAB, т. е. треугольник FAB равнобедренный, поэтому FB = AB.

Из того, что AF || BD вытекает пропорция:

FB/BC = AD/DC

Заменяя FB равным отрезком AB, получим пропорцию:

AB/BC = AD/DC (ЧТД).

Теорема 99 (обратная 98). Прямая, проведенная из вершины треугольника и делящая противоположную сторону на части, пропорциональные двум другим сторонам, делит угол при вершине пополам.

Дано. В треугольнике ABC (черт. 159) прямая BD рассекает противоположную сторону так, что имеет место пропорция:

AB/BC = AD/DC (a)

Требуется доказать, что ∠α = ∠β.

Доказательство. Проведем отрезок AF параллельно BD, тогда из треугольника AFC вытекает пропорция:

FB/BC = AD/DC (b)

Сравнивая две пропорции (a) и (b), заключаем, что FB = AB, следовательно,

∠AFB = ∠FAB.

Так как ∠α = ∠FAB, ∠β = ∠AFB, то и

∠α = ∠β (ЧТД).

Отношения в прямоугольном треугольнике

Теорема 100. Перпендикуляр, опущенный из вершины прямого угла на гипотенузу, среднепропорционален между частями гипотенузы.

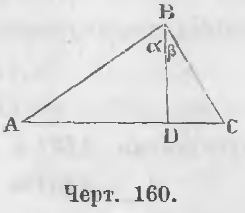
Дано. В треугольнике ABC угол ABC прямой (черт. 160) и BD ⊥ AC.

Требуется доказать, что AD/BD = BD/DC.

Доказательство. Треугольники ABD и BDC подобны, ибо углы при точке D равны как прямые; кроме того из равенств ∠A + ∠α = d, ∠α +∠β = d вытекает

A + α = α + β, или A = β, следовательно и C = α.

Из подобия треугольников ABD и BDC вытекает пропорция

AD/BD = BD/DC (ЧТД).

Примечание. Если составляют одно отношение из сторон одного треугольника, то другое отношение составляется из соответственных сторон другого треугольника. При этом рассуждают следующим образом: против стороны AD лежит угол α, которому в подобном треугольнике BCD равен угол C, а против него лежит сходственная сторона BD треугольника BCD и т. д.

Теорема 101. Каждый катет среднепропорционален между целой гипотенузой и отрезком, прилежащим катету.

Доказательство. a) Треугольники ABC и ABD (черт. 160) подобны, ибо ∠ABC = ∠ADB как прямые, ∠A общий, следовательно,

∠C = ∠α

Из подобия треугольников вытекает пропорция:

AD/AB = AB/AC (a)

b) Треугольники ABC и BCD подобны, ибо ∠ABC = ∠BDC как прямые, ∠C общий, следовательно,

∠A = ∠β, откуда
DC/BC = BC/AC (b)

Теорема 102. Квадрат гипотенузы равен сумме квадратов катетов.

Из предыдущих пропорций (a) и (b) вытекают равенства:

AB² = AD · AC
BC² = DC · AC

Складывая их, получим:

AB² + BC² = AD · AC + DC · AC или
AB² + BC² = AC (AD + DC) = AC · AC = AC², т. е.
AC² = AB² + BC²

откуда

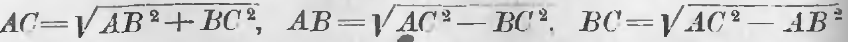
a) Гипотенуза равна корню квадратному из суммы квадратов катетов.

b) Катет равен корню квадратному из квадрата гипотенузы без квадрата другого катета.

Теорема 103. Диагональ квадрата несоизмерима с его стороной, или гипотенуза равнобедренного прямоугольного треугольника несоизмерима с катетом.

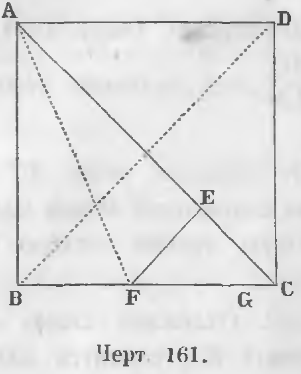
Дано. В квадрате ABCD проведена диагональ AC (черт. 161).

Требуется доказать, что отношение AC/AD есть величина несоизмеримая.

Доказательство. Станем сравнивать больший отрезок AC с меньшим BC по обыкновенным приемам нахождения общей меры, т. е. наложим меньший отрезок на больший, первый остаток на меньший и т. д.

a) Наложим отрезок BC на отрезок AC. Отложив отрезок AE, равный AB или BC, мы видим, что отрезок BC уложился один раз, ибо

AB + BC > AC.

Так как AB = BC, то 2BC > AC и BC > ½AC, следовательно, первый остаток EC < BC.

b) Наложим первый остаток EC на отрезок BC. Для этого из точки E восставим перпендикуляр EF и соединим точку F с A.

c) Треугольник FEC равнобедренный, ибо ∠EFC = ∠BAC как углы с перпендикулярными сторонами

∠BAC = ∠ECF, следовательно,
∠EFC = ∠ECF

На этом основании стороны EF и EC равны:

EF = EC (1)

Треугольники ABF и AEF равны, ибо они прямоугольны и у них

AF сторона общая
AB = AE по построению, следовательно,
BF = EF (2)

Таким образом из равенств (1) и (2) выходит, что

EC = EF = BF

Не трудно видеть, что первый остаток укладывается в отрезке BC не более двух раз. Отложив EC два раза на отрезке BC, найдем точку G и второй остаток GC. Таким образом, остаток после наложения сторон квадрата на диагональ укладывается в стороне квадрата не более двух раз.

d) Наложим второй остаток GC на первый EC.

В прямоугольном и равнобедренном треугольнике FEC соотношение между отрезками GC, FC и EC то же самое как и соотношение между данными отрезками EC, AC и BC в треугольнике ABC, ибо треугольник FEC прямоугольный и равнобедренный, следовательно, при дальнейшем наложении мы будем снова получать остаток. Продолжая так поступать, мы всегда будем получать остатки, поэтому общей меры мы никогда не получим, следовательно, отрезки AC и BC несоизмеримы.

Обозначив длину диагонали черед l, длину стороны квадрата через a, последовательные величины остатков через d₁, d₂ и т. д., т. е. положив

AC = l, BC = a, CE = d₁, GC = d₂ и т. д.

имеем равенства:

l = a + d₁, a = 2d₁ + d₂, d₁ = 2d₂ + d₃ и т. д.

откуда

l/a = 1 + d₁/a
a/d₁ = 2 + d₂/d₁ или d₁/a = ½ + d₂/d₁
d₁/d₂ = 2 + d₃/d₂ или d₂/d₁ = ½ + d₃/d₂

следовательно,

l/a = 1 + ½ + ½ + …

Отношение между длинами l и a выражается бесконечной непрерывной дробью. Несоизмеримость впрочем прямо вытекает из выражения диагонали квадрата по катетам.

Действительно,

AC² = AB² + BC².

Так как AB = BC, то AC² = 2AB², откуда AC = AB√2 и AC/AB = √2 величина несоизмеримая.

Соотношение между сторонами остроугольного и тупоугольного треугольника

Теорема 104. Квадрат стороны, лежащей против острого угла, равен сумме квадратов прочих двух сторон треугольника без удвоенного произведения основания на отрезок, заключающийся между вершиной острого угла и высотой.

Здесь могут быть два случая: 1) когда перпендикуляр, выражающий высоту, пойдет внутри и 2) когда он пойдет вне треугольника.

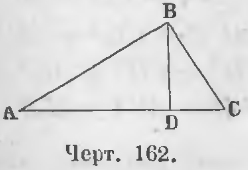
Первый случай. Перпендикуляр BD (черт. 162), опущенный из вершины B на основание AC треугольника ABC, пойдет внутри треугольника.

Требуется доказать, что AB² = BC² + AC² - 2AC · DC.

Доказательство. Для прямоугольного треугольника ABD имеем равенство:

AB² = BD² + AD² (a)
AD = AC - DC, AD² = (AC - DC)² = AC² + DC² - 2AC · DC

Из прямоугольного треугольника BDC имеем:

BD² = BC² - DC²

Вставляя величины BD² и AD² в равенство (a), получим:

AB² = BC² - DC² + AC² + DC² - 2AC · DC, откуда
AB² = BC² + AC² - 2AC · DC (ЧТД).

2-й случай. Перпендикуляр BD (черт. 163) лежит вне треугольника ABC.

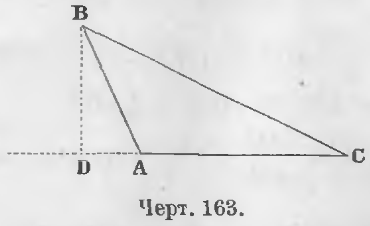
Доказательство. Из прямоугольного треугольника ABD имеем:

AB² = BD² + DA²

Из прямоугольного треугольника BCD имеем:

BD² = BC² - CD²

следовательно,

AB² = BC² - CD² + DA².

Так как

DA = CD - AC
DA² = (CD - AC)² = CD² + AC² - 2CD · AC, то
AB² = BC² - CD² + CD² + AC² - 2CD · AC, откуда
AB² = BC² + AC² - 2CD · AC (ЧТД).

Теорема 105. Квадрат стороны, лежащей против тупого угла, равен сумме квадратов прочих двух сторон треугольника с удвоенным произведением основания на отрезок его от вершины тупого угла до высоты.

Дано. В тупоугольном треугольнике ABC отрезок CD (черт. 164) есть отрезок, лежащий между вершиной тупого угла и высотой.

Требуется доказать, что

AB² = AC² + BC² + 2AC · CD

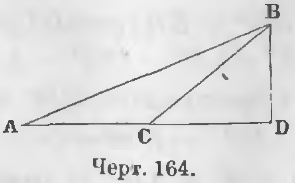
Доказательство. Из тупоугольного треугольника ABC имеем:

AB² = BD² + AD² (a)
AD = AC + CD, AD² = AC² + CD² + 2AC · CD

Из прямоугольного треугольника BCD вытекает, что

BD² = BC² - CD²

Заменяя AD² и BD² в равенстве (a), получим:

AB² = BC² - CD² + AC² + CD² + 2AC · CD

откуда

AB² = BC² + AC² + 2AC · CD (ЧТД).

Теорема 106. Сумма квадратов диагоналей равна сумме квадратов всех четырех сторон параллелограмма.

Дан параллелограмм ABCD (черт. 165) и проведены его диагонали AC и BD.

Требуется доказать, что

AC² + BD² = AB² + BC² + CD² + AD²

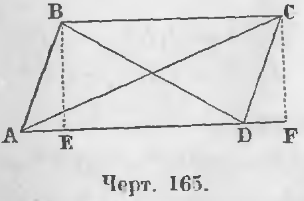
Доказательство. Опустив перпендикуляры BE и CF, имеем из косоугольного треугольника ABD равенство:

BD² = AB² + AD² - 2AD · AE (1)

Из тупоугольного треугольника ACD равенство:

AC² = CD² + AD² + 2AD · DF (2)

Отрезки AE и DF равны, ибо прямоугольные треугольники ABE и DCF равны, так как они имеют по равному катету и равной гипотенузе.

Сложив равенства (1) и (2), имеем:

BD² + AC² = AB² + AD² + CD² + AD²

Так как AD = BC, то

BD² + AC² = AB² + BC² + CD² + AD² (ЧТД).

Теорема 107. Сумма квадратов двух сторон треугольника равна сумме удвоенного квадрата отрезка, соединяющей вершину с серединой основания, с удвоенным квадратом половины основания.

Дано. Соединим вершину B с серединой основания D треугольника ABC так, что AD = DC (черт. 166).

Требуется доказать, что

AB² + BC² = 2AD² + 2BD²

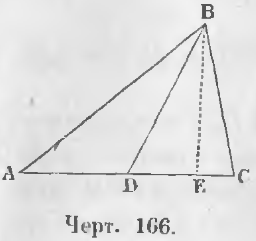
Доказательство. Проведем высоту BE.

Из прямоугольных треугольников ABE и BCE вытекают равенства:

AB² = BE² + AE²
BC² = BE² + CE²

Сложив их, находим:

AB² + BC² = 2BE² + AE² + CE² (a)

Так как AE = AD + DE = CD + DE, CE = CD - DE, то

AE² = (CD + DE)² = CD² + DE² + 2CD · DE
CE² = (CD - DE)² = CD² + DE² - 2CD · DE

откуда

AE² + CE² = 2CD² + 2DE² (b)

Заменяя в равенстве (a) сумму AE² + CE² из равенства (b), имеем:

AB² + BC² = 2BE² + 2CD² + 2DE².

Из прямоугольного треугольника BDE видно, что

BE² = BD² - DE²

следовательно

AB² + BC² = 2BD² - 2DE² + 2CD² + 2DE²

откуда

AB² + BC² = 2BD² + 2CD² (ЧТД).