196. Площадью вообще называется определенная, ограниченная со всех сторон часть плоскости. В главе XVI мы занимались вопросами о сравнении площадей, ограничиваемых прямыми линиями и об их сложении. Мы можем, если даны нам 2 многоугольника, имеющие площадь, узнать, равны ли эти площади или одна из них больше другой (можно, напр., каждый многоугольник превратить в равновеликий ему треугольник, потом один из полученных треугольников превратить в равновеликий ему, имеющий такое же основание, как и другой треугольник, и тогда вопрос, какая из двух площадей больше, сведется к вопросу, высота у какого треугольника больше), и можем построить многоугольник, равновеликий сумме двух данных. Этих условий, как мы знаем, достаточно для того, чтобы можно было площади, ограничиваемые прямыми линиями, выражать числами, принимая одну из них за единицу.

Итак, если имеем две площади A и B, ограниченные прямыми линиями (площади двух многоугольников), то для них можно составить уравнение A = kB или A/B = k, где k какое-либо число: рациональное (целое или дробное), если площадь A соизмерима с площадью B, или иррациональное, если площади A и B несоизмеримы.

Может возникнуть вопрос: может быть, признавая отношение двух площадей (A/B), в случае несоизмеримости этих площадей, равным особому числу, мы этим самым вводим еще новые числа, не те, которые мы называли иррациональными и признали существующими, рассматривая отношение двух несоизмеримых отрезков.

Не трудно дать ответ на этот вопрос. Превратим два данных многоугольника, площади которых мы назвали через A и B, в равновеликие им треугольники (п. 159 задание 2), каждый из этих треугольников в равновеликий ему прямоугольник с тем же основанием (п. 156 добавление), а каждый из этих прямоугольников в равновеликий ему такой, чтобы у обоих прямоугольников получились одинаковые основания (см. чер. G); пусть тогда высоты этих прямоугольников суть, h и h', а площади их равны соответственно площадям данных многоугольников, т. е. A и B. Рассмотрим два отношения: 1) h/h' и 2) A/B. Найдем самое большое число со знаменателем n, чтобы оно было меньше первого отношения (h/h'). Для этого разделим h' на n равных частей и станем эти части откладывать на h, – пусть их уложится m с остатком x (здесь имеем место аксиома Архимеда), причем x < h'/n. Тогда искомое число есть m/n (мы видим также, что (m+1)/n есть самое малое число со знаменателем n, большее h/h').

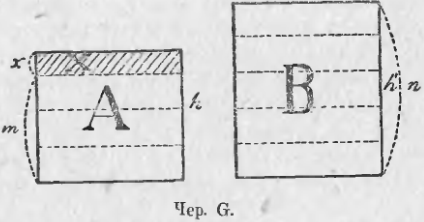
Построив через точки деления высот h' и h ряд прямых, параллельных основаниям прямоугольников, мы получим, что площадь B разделится на n равных частей и таких частей на площади A уложится m с остатком X (площадь X меньше 1/n части площади B, ибо X есть площадь прямоугольника с таким же основанием, но с меньшею высотою, - площадь X при наложении займет лишь часть площади 1/n B).

Поэтому, мы найдем, что (A – X)/B = m/n, но A > A – X, следовательно A/B > m/n или m/n < A/B. Итак, даже самое большое число со знаменателем n, меньшее первого отношения (h/h'), оказалось меньше также второго отношения (A/B). Также, если бы мы взяли число (m+1)/n, самое малое число со знаменателем m больше отношения h/h', то здесь же увидали бы, что оно также больше A/B. Отсюда заключаем, что нельзя найти такого рационального числа, чтобы оно было больше одного из наших отношений и меньше другого, т. е. мы должны признать, что наши два отношения равны одному и тому же числу, или что A/B = h/h'. Таким образом отношение площадей A и B равно отношению двух отрезков. Поэтому мы должны признать, что отношение двух несоизмеримых площадей равняется одному из тех же иррациональных чисел, какие мы ввели при изучении отношений отрезков.

Иное дело, если мы обратимся к площадям, ограниченным не только прямыми, но и кривыми линиями: здесь у нас нет способа сравнивать две такие площади и вопрос об измерении таких площадей может быть разрешен лишь косвенными приемами.

Здесь мы будем заниматься измерениями площадей, ограниченных только прямыми линиями.

197. Надо, прежде всего, выбрать какую-либо площадь за единицу. Принято за единицу для измерения площадей считать площадь такого квадрата, каждая сторона которого равна линейной единице; такая площадь называется квадратною единицею (см. чер. 199). Общеупотребительны: квадратный аршин — площадь такого квадрата, каждая сторона которого равна линейному аршину, квадратный фут, квадратный метр и т. д.

Необходимо еще для непосредственного измерения площади уметь откладывать на измеряемой площади ту, которая принята за единицу. Хотя с точки зрения теории это не доставляет затруднений (на основании главы XVI), но на практике такой способ был бы крайне неудобен. Оказывается, что, благодаря тому выбору единицы для измерения площадей (площадь квадрата, у которого каждая сторона равна линейной единице), который был нами сделан, вопрос об измерении площади сводится к вопросу об измерении отрезков.

198. Основною задачею является измерение площади прямоугольника.

Пусть имеем прямоугольник ABDC (чер. 200), площадь которого надо измерить данною квадратною единицею M.

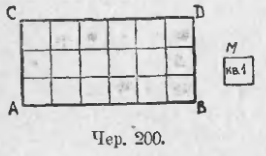
Рассмотрим сначала случай, когда сторона квадрата M, т. е. линейная единица, укладывается по целому числу раз на основании AB прямоугольника и на его высоте AC. Если, например (как на чертеже), эта линейная единица укладывается на основании AB — 6 раз и на высоте AC — 3 раза, то, построив ряд параллельных, мы можем разбить измеряемую площадь на 3 плосы, высота каждой из которых равна линейной единице, а каждую полосу на 6 квадратных единиц. Всего квадратных единиц получим 6 * 3 = 18. Следовательно, измеряемая площадь равна 18 квадратным единицам.

Вообще, пусть найдем:

AB = a лин. един.,
AC = h лин. един.,

где числа a и h целые; тогда, построив ряд параллельных основанию, разобьем площадь прямоугольника на h полос, а, построив ряд параллельных высоте прямоугольника, разобьем каждую полосу на a квадратных единиц. Следовательно, вся измеряемая площадь найдется умножением чисел a и h, т. е.:

Площ. ABDC = (ah) квадр. един.

Результат можно прочесть словами:

Число, выражающее площадь прямоугольника в квадратных единицах, равно произведению чисел, выражающих его основание и высоту в соответственных линейных единицах.

Но пока в этом мы убедились лишь для случая, когда от измерения основания и высоты получаются целые числа.

Далее рассмотрим случай, когда стороны прямоугольника соизмеримы с линейною единицею, но эта последняя не укладывается по целому числу раз на основании и высоте прямоугольника. Тогда мы знаем, что от их измерения нашею линейною единицею получаются дробные числа. Пусть, например (чер. 201),

AB = 1¾ лин. един.,
AC = 7/8 лин. един.

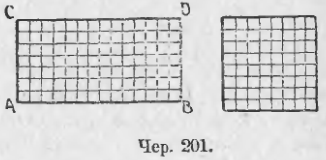
Мы можем всегда привести полученные дроби к общему знаменателю и, кроме того, станем нашу линейную единицу называть главною, также и соответствующую квадратную — главною квадратною единицею; тогда для нашего примера имеем:

AB = 1 + 6/8 глав. лин. един. = 14/8 глав. лин. един.
AC = 7/8 глав. лин. един.

Построим теперь такой квадрат, сторона которого равна 1/8 доли глав. лин. единицы и назовем площадь этого квадрата побочною квадратною единицею. На чертеже главная квадратная единица разделена на побочные: их укладывается в главной 64 (8 * 8, что легко сосчитать на основании предыдущего случая). Следов., 1 побоч. квадр. Единица = 1/64 глав. квадр. един. Выразим теперь площадь нашего прямоугольника ABDC в побочных квадратных единицах. Мы видим, что

AB = 14 побоч. лин. един.,
AC = 7 побоч. лин. един.

Так как теперь получились целые числа, то применим сюда предыдущий случай, и мы имеем:

Площ. ABDC = (14 * 7) побоч. квад. един.

Переведем теперь полученное число в главные квадратные единицы, зная, что побоч. квадр. един. = 1/64 глав. квадр. един.

Тогда получим:

Площ. ABDC = (14 * 7) / 64 глав. квадр. ед. = (14/8 * 7/8) глав. квадр. ед. = (1¾ * 7/8) глав. квадр. ед.

Видим, что результат предыдущего случая подтверждается и на этом примере.

Пусть теперь вообще

AB = a главн. лин. един.,
AC = h главн. лин. един.,

где a и h суть дробные числа. Положим, что, после приведения этих дробей к общему знаменателю, получим:

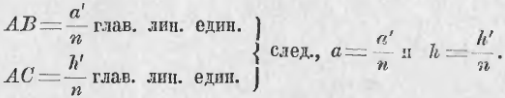
Разделим главную линейную единицу на n равных частей и 1/n долю этой единицы назовем побочною линейною единицею; затем построим квадрат, сторона которого равна этой побочной линейной единице, - его площадь назовем побочною квадратною единицею. Тогда в главной квадратной единице умещается n² побочных квадратных единиц (n * n — согласно предыдущему случаю). Будем выполнять измерение в побочных единицах; тогда

AB = a' побоч. лин. един.,
AC = h' побоч. лин. един.,

где числа a' и h' — целые. Поэтому, согласно первому разобранному нами случаю, имеем:

Площ. ABDC = (a' * h') побоч. квадр. един.

Так как 1 побоч. квадр. един. = 1/n2 глав. квадр. един., то площ. ABDC = (a'h')/n2 глав. квадр. един. = (a'/n * h'/n) главн. квадр. един. = (ah) гл. кв. ед.

Итак, между числами, выражающими площадь и стороны прямоугольника в соответствующих единицах, и для этого случая имеет место вышенайденная зависимость.

199. Эта зависимость распространяется и на случай, когда стороны прямоугольника (или, по крайней мере, одна из них) несоизмеримы с линейною единицею. В этом случае имеем:

AB = a лин. един.,
AC = h лин. един.,

где a и h (или одно из них) суть иррациональные числа. Мы можем измерить наши стороны с какою угодно точностью, например, до 1/n. Для этого разделим линейную единицу на n равных частей и, откладывая эти части по сторонам AB и AC, для каждой из них найдем по 2 отрезка, соизмеримых с единицею, из которых один меньше, а другой больше соответствующей стороны и разность между которыми = 1/n доли единицы. Пусть меньшие из этих отрезков выражаются числами a' и h'; тогда большие выражаются числами a' + 1/n и h' + 1/n, и мы имеем

a' < a < a' + 1/n и h' < h < h' + 1/n',

где a' и h' суть рациональные числа — дроби со знаменателем n.

Мы можем построить теперь два прямоугольника, стороны которых соизмеримы с единицею и площади которых можно вычислить по формуле п. 198: один внутренний по отношению к данному прямоугольнику, стороны которого выражаются числами a' и h', и другой внешний, стороны которого выражаются числами a' + 1/n и h' + 1/n. Тогда площадь первого выражается числом a' * h' и площадь второго – числом (a' + 1/n)(h' + 1/n). Разность этих площадей выражается числом

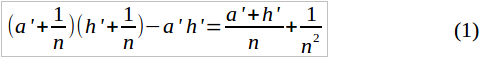
Так как площадь данного прямоугольника заключена между площадями двух построенных прямоугольников, то разность между площадями данного и одного из построенных должна выразиться числом, меньшим только что найденного. Поэтому заключаем:

1) Измерив площадь, например, внутреннего прямоугольника и приняв ее за приближение к площади данного, мы делаем ошибку, меньшую выше найденной разности, – последняя служит, следовательно, пределом этой ошибки. Увеличивая число n (а его мы можем выбрать по своему произволу), мы можем сделать этот предел как угодно малым: знаменатели дробей в выражении (1) могут быть сделаны сколь угодно большими, а числители остаются меньше определенного числа (всегда a' < a и h' < h).

2) Чтобы найти точное числовое выражение для площади нашего прямоугольника, надо найти такое число, которое было бы всегда заключено между рациональными числами a' * h' и (a' + 1/n) * (h' + 1/n), как бы велико n ни было, так как площадь данного прямоугольника всегда заключена между площадями соответствующих внутреннего и внешнего прямоугольника. Теория иррациональных чисел учит, что таким числом является произведение a * h, для которого рациональные числа a' * h' и (a' + 1/n) (h' + 1/n), служат приближениями (первое с недостатком, второе с избытком), предел погрешности которых может быть найден и увеличением числа n может быть сделан как угодно мал.

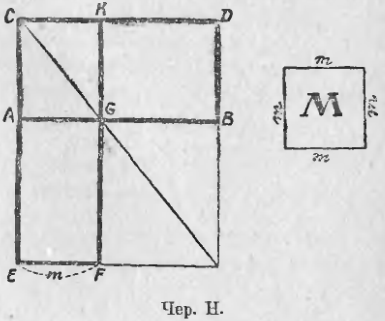
Что такое число существует, ясно из п. 198: отношение всяких двух площадей, ограниченных прямыми линиями, а, следовательно, и отношение площади нашего прямоугольника ABDC к квадратной единице может быть признано равным отношению двух отрезков, а последнее всегда признается нами за определенное число, рациональное или иррациональное. Чер. H, где M обозначает площадь, принимаемую за квадратную единицу, а m — отрезок, принимаемый за линейную единицу, построен так, как сказано в зад. 1 п. 159. Поэтому здесь получаем, что прямоугольник CKFE (основание которого EF = m) равновелик данному прямоугольнику ABDC. Поэтому пл. ABDC / M = пл. CKFE / M = CE / m (последнее на основании п. 196: площади CKFE и M можно рассматривать, как площади прямоугольников, имеющих равные основания m и различные высоты (CE и m).

Итак, во всех случаях имеем, называя число, выражающее площадь прямоугольника в квадр. един., чрез Q:

Q = a * h.

Подробно эта формула читается:

Число, выражающее площадь прямоугольника в квадратных единицах, равно произведению чисел, выражающих его основание и высоту в соответствующих линейных единицах.

Коротко, хотя и неправильно, читают:

Площадь прямоугольника равна произведению его основания на высоту.

200. Мы знаем (п. 154), что параллелограмм равновелик прямоугольнику, имеющему такие же основание и высоту; поэтому теперь имеем (выражая сокращенно):

Площадь параллелограмма равна произведению его основания на высоту.

201. Мы знаем (п. 156), что площадь треугольника равна половине площади параллелограмма, имеющего такие же основание и высоту. Поэтому:

Площадь треугольника равна половите произведения его основания на высоту.

Площадь прямоугольного треугольника равна половине произведения его катетов (один катет примем за основание; тогда другой явится его высотою).

202. Из п. 163 мы знаем, что трапеция равновелика треугольнику, имеющему такую же высоту, основанием которого служит сумма параллельных сторон трапеции. Поэтому имеем:
Площадь трапеции равна половине произведения суммы ее параллельных сторон на высоту;
или:
Площадь трапеции равна произведению ее средней линии на высоту.
203. Найдем еще, как измерить площадь правильного многоугольника.

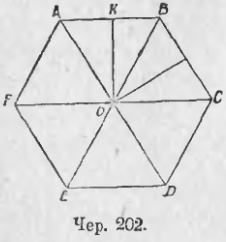
Пусть имеем правильный многоугольник ABCDEF (чер. 202). Найдем его центр O (п. 151) и соединим точку O с вершинами A, B, C и т. д. многоугольника. Тогда увидим, что площадь многоугольника слагается из площадей треугольников OAB, OBC и т. д. Примем сторону AB в ∆AOB за основание и пусть от измерения AB линейною единицею получится число a. Построим высоту OK и ∆OAB — OK является, как мы знаем, апофемою нашего правильного многоугольника — и назовем через p число, полученное от измерения апофемы OK линейною единицею.

Тогда площ. ∆AOB = (a * p) / 2 квадр. един. (п. 199).

Пусть сторон у нашего многоугольника n; тогда и треугольников получается тоже n и они все равны между собою. Следовательно, площадь многоугольника выразится числом 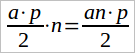, или, называя через Q число, выражающее площадь в квадратных единицах, имеем:

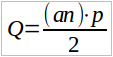
Здесь множители a и n мы заключили в скобки, чтобы показать, что мы их произведение хотим считать за одно число: число a выражает одну сторону многоугольника, но у многоугольника n сторон и все они равны между собою, – следовательно,

AB + BC + CD + DE + … = AB * n

Сумма всех сторон многоугольника называется его периметром (п. 79); следовательно, число a * n выражает периметр нашего многоугольника в линейных единицах. Поэтому:

число, выражающее площадь правильного многоугольника в квадратных единицах, равно половине произведения чисел, выражающих его периметр и апофему в соответствующих линейных единицах,

или, сокращенно:

Площадь правильного многоугольника равна половине произведения его периметра на апофему.

204. Чтобы измерить площадь какого-нибудь многоугольника, разбивают его на треугольники, измеряют отрезки, нужные для вычисления площадей полученных треугольников и трапеций, и затем вычисляют площади каждого треугольника и каждой трапеции.

205. Упражнения.

1. Периметр прямоугольника равен 40 дм., а его высота составляет 2/3 его основания. Вычислить его площадь.

2. Стороны параллелограмма равны соответственно 20 и 25 дм., а высота, опущенная на меньшую сторону, равна 15 дм. Вычислить другую высоту этого параллелограмма.

3. Две стороны треугольника равны соответственно 18 и 12 дм., а высота, опущенная на большую из них, равна 20 дм. Вычислить высоту, опущенную на меньшую из данных сторон.

4. Вычислить площадь квадрата, описанного около круга, радиус которого равен 8 сант.

5. Прямоугольник равновелик сумме площадей двух треугольников, основание одного из которых равно 12 сант. и высота равна 8 сант., а основание и высота другого, каждая в 2 раза меньше соответствующего основания и высоты первого. Вычислить высоту этого прямоугольника, если его основание равно среднему арифметическому между основаниями треугольников.

6. Площадь трапеции равна 80 квадр. дм. и ее высота равна 8 дм. Вычислить ее параллельные стороны, если одна из них на 4 дм. больше другой.

7. Высота треугольника равна 17 дм., а средняя линия этого треугольника, перпендикулярная к указанной высоте, равна 6 дм. Вычислить площадь этого треугольника.

В следующих задачах не указано, какими именно линейными и какими квадратными единицами произведено измерение. Само собою разумеется, что площадь выражается в квадратных единицах, а отрезки — в линейных; в каждой задаче квадратные и линейные единицы должны быть соответствующими друг другу.

8. Вычислить площадь ромба, если его диагонали равны соответственно 46 и 30.

9. Площадь трапеции равна 90, ее высота равна 10. Вычислить ее параллельные стороны, если одна из них в 2 раза больше другой.

10. Вычислить площадь квадрата, вписанного в круг, принимая за единицу площадь квадрата, сторона которого равна радиусу круга. (Разбить квадрат диагональю на 2 треугольника).