273. Мы владеем представлением о длине кривой линии. Если мы имеем какую-либо кривую (чер. 266), то мы представляем, что эту кривую возможно выпрямить и получить прямолинейный отрезок. Этот отрезок и есть длина нашей кривой, - ее можно выразить числом, принимая другой какой-либо отрезок за единицу. Однако мы не можем построить прямолинейный отрезок, выражающий длину данной кривой. Тем не менее, не следует отказываться от решения задачи: выразить длину данной кривой числом, принимая за единицу определенный прямолинейный отрезок, - косвенным путем возможно прийти к решению этой задачи. В курсе элементарной геометрии рассматривается лишь вопрос о длине окружности или ее дуги.
Подобно этому, часть плоскости может быть ограничена кривою линиею (или несколькими линиями). Мы видим, напр., на чер. 267, что имеющаяся там кривая выделяет из плоскости определенную площадь, но мы не можем построить равную ей площадь, ограниченную прямыми линиями. Однако, косвенным путем можно прийти к решению задачи: выразить площадь, ограниченную кривою линиею, числом, принимая за единицу площадь определенного квадрата. В элементарной геометрии рассматривается вопрос о площади, ограничиваемой кругом, или о площадях, ограниченных дугою круга и прямыми линиями (или даже о площадях, ограниченных несколькими дугами одного или различных кругов и несколькими прямыми линиями).
274. Остановимся сначала на предварительных соображениях.
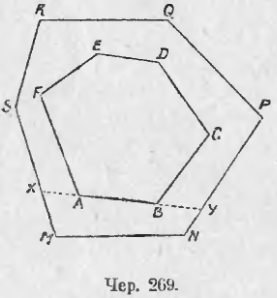
1. Пусть в круг (чер. 268) вписан правильный многоугольник и около круга описан одноименный с ним правильный многоугольник. Тогда мы видим, что AB < AM + MB; BC < BN + NC и т. д. Отсюда (складывая эти неравенства по частям) приходим к заключению, что периметр вписанного многоугольника меньше периметра описанного.
Возможно также показать, что периметры правильных вписанных многоугольников с увеличением числа сторон увеличиваются, а периметры правильных описанных многоугольников — уменьшаются. Например, остановимся на случае, когда число сторон вписанного и описанного правильных многоугольников удваивается. Для удвоения числа сторон наших правильных многоугольников следует разделить пополам каждую из дуг AB, BC и т. д. (чер. 268). Пусть, например, P есть середина дуги AB. Соединив P с A и с B, получим две стороны AP и PB нового вписанного многоугольника. Мы увидим, что при удвоении числа сторон каждая сторона (например, AB) прежнего вписанного многоугольника заменяется ломаною (AP + PB), составленною из двух сторон нового многоугольника. Отсюда ясно, что периметр нового многоугольника больше периметра прежнего.
Построив затем в точке P касательную KL к кругу, мы получим сторону KL нового описанного многоугольника. Чтобы перейти от периметра прежнего описанного многоугольника к периметру нового, мы должны сделать ряд замен, одною из которых является следующая: надо ломаную KML заменить прямолинейным отрезком KL. Отсюда заключаем, что периметр правильного описанного многоугольника при удвоении числа его сторон уменьшается.
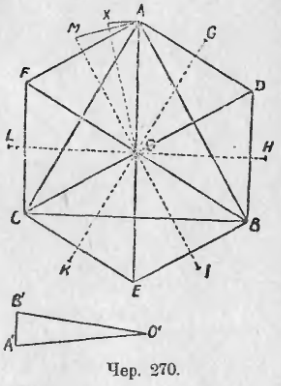
2. Рассмотрим 2 каких-нибудь выпуклых многоугольника, причем все вершины одного лежат внутри другого. Пусть ABCDEF и MNPQRS (чер. 269) суть такие многоугольники. Тогда продолжим одну из сторон BA внутреннего многоугольника до пересечения в точках X и Y со сторонами внешнего. МЫ видим, что точки A и B соединены двумя выпуклыми ломаными: объемлемой AFEDCB и объемлемой AXSRQPYB. На основании свойств таких ломаных (п. 94) имеем:
BC + CD + DE + EF + FA < BY + YP + PQ + QR + RS + SX + XA
Рассматривая теперь точки X и Y, мы также найдем:
XA + AB + BY < XM + MN + NY.
Складывая по частям эти неравенства, найдем
BC + CD + DE + EF + FA + XA + AB + BY < BY + YP + PQ + QR + RS + SX + XA + XM + MN + NY.
Мы видим, что можно вычесть из обеих частей этого неравенства одинаковые отрезки XA и BY. Можно также заменить SX + XM через SM и NY + YP через NP. Поэтому получим
BC + CD + DE + EF + FA + AB < PQ + QR + RS + SM + MN + NP,
т. е. периметр внутреннего выпуклого многоугольника меньше периметра внешнего.
Это свойство остается в силе, если внешний многоугольник и не выпуклый.
Тоже свойство остается в силе, когда некоторые из вершин внутреннего многоугольника (или даже все) расположены на сторонах внешнего.
Можно сейчас же применить полученное свойство к периметрам вписанного в круг и описаны около него многоугольников:
Периметр всякого вписанного в круг многоугольника меньше периметра описанного около того же круга многоугольника.
В частном случае отсюда вытекает:
Периметр всякого вписанного в круг многоугольника меньше периметра описанного около того же круга квадрата, т. е. меньше 8R (последнее потому, что сторона описанного квадрата равна диаметру круга или 2R).
3. Мы можем вписать в данных круг правильный многоугольник такой, чтобы его сторона была меньше любого, наперед данного отрезка.
Пусть, например, в круг, радиус которого = OA = OB = OC (чер. 270, на чертеже самый круг не дан) вписан правильный треугольник ABC; затем, удвоив число сторон, получим правильный вписанный 6-угольник ADBECF, затем 12-угольник AGDHBIEKCLFM и т. д.
Обратим внимание на то, что при нашем процессе мы всякий раз строим центральный угол, опирающийся на сторону нового многоугольника, в 2 раза меньший, чем предыдущий таковой же центральный угол, например, ∠AOM = ½ ∠AOF. Этим процессом деления угла пополам мы можем сделать центральный угол, опирающийся на сторону многоугольника как угодно малым. Пусть теперь нам дан отрезок A'B'; построим на нем равнобедренный ∆A'O'B' так, чтобы O'A' = O'B' = OA. Станем полученный ∠A'O'B' откладывать на угле, например, AOF и пусть он уложиться m раз с остатком.
Мы можем затем разделить угол AOF на 2n частей, чтобы 2n > m (выбрать такое число n всегда возможно); тогда одна такая часть, например, ∠AOX, должна быть меньше ∠A'O'B'. Два треугольника A'O'B' и AOX имеют по две равных сторон O'A' = O'B' = OA = OX (мы, конечно, разделяя последовательно пополам получаемые центральные углы, всякий раз откладываем на биссекторах отрезки равные радиусу и поэтому OX = OA), но углы между ними не равны, - тогда сторона AX, лежащая против меньшего угла, должна быть меньше стороны A'B', т. е. нам удалось процессом удваивания числа сторон дойти до такого многоугольника, каждая сторона которого меньше данного отрезка A'B', как бы мал он ни был, другими словами, процессом удваивания можно получить такой правильный многоугольник, расстояние между двумя соседними вершинами которого меньше любого данного отрезка.
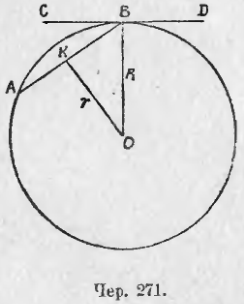
4. Пусть теперь вписан в круг правильный многоугольник об n сторонах и описан около круга одноименный с ним многоугольник, пусть AB и CD (чер. 271) суть их стороны. Построим апофемы OB и OK этих многоугольников и назовем OK через r (апофема вписанного многоугольника) и OB через R (апофема описанного многоугольника и в тоже время радиус нашего круга). Тогда из ∆OKB имеем OB – OK < KB (разность двух сторон треугольника — a меньше третьей стороны). Так как KB = AB/2, то R – r < AB/2. Так как мы можем, согласно предыдущему, вписать в круг такой правильный многоугольник, чтобы его сторона была меньше любого данного отрезка, как бы мал он ни был, то отсюда заключаем, что можно вписать в круг такой правильный многоугольник, чтобы разность между радиусом круга и апофемою этого вписанного правильного многоугольника оказалась меньше любого данного отрезка, как бы мал он ни был.
5. Назовем периметр вписанного правильного n-угольника через pn и периметр описанного правильного n-угольника через Pn.
Тогда, согласно п. 248, имеем
Pn/pn = R/r
(отношение периметров правильных одноименных многоугольников равно отношению их апофем).
Отсюда мы можем (п. 177 добавление) получить следующую пропорцию
(Pn – pn)/Pn = (R – r)/R.
Отсюда (п. 178) вытекает
(Pn – pn) / (R – r) = Pn/R.
Ограничимся здесь рассмотрением лишь одного случая, а именно положим, что здесь речь идет лишь о правильных многоугольниках, получающихся при помощи процесса удваивания числа сторон, начиная с правильного вписанного и описанного четырехугольника. Тогда на основании пункта 1-го этого п. периметры следующих правильных описанных многоугольников будут каждый меньше SR (периметра описанного квадрата). Поэтому и здесь мы будем считать Pn < 8R. Если мы предыдущий член второго отношения последней пропорции заменим через 8R, то это отношение увеличится и тогда будем иметь
(Pn – pn) / (R – r) < 8R/R.
Но отношение 8R/R равно числу 8. Поэтому
(Pn – pn) / (R – r) < 8.
Это неравенство можно написать в форме:
Pn – pn < 8(R – r).
Пусть нам дан какой-либо отрезок k. Тогда, согласно пункту 4 этого п., мы достигнем того, чтобы R – r было меньше k/8, если построим такой вписанный правильный многоугольник, чтобы его сторона была меньше k/4 (что возможно, согласно пункту 3). Тогда, построив такой вписанный и соответствующий ему описанный многоугольники, мы получим:
Pn – pn < 8 · k/8 или Pn – pn < k,
т. е. можно вписать в круг и описать около него такие правильные одноименные многоугольники, чтобы разность их периметров была меньше любого данного отрезка, как бы мал он ни был.
275. Обратимся теперь к соображениям, которые позволят решить задачу о выражении числом длины круга и линейных единицах.
Пусть имеем круг O (чер. на стран. 284), радиус которого равен R. Станем вписывать в этот круг и описывать около него различные многоугольники (в том числе и правильные). Мы можем периметры этих многоугольников выпрямить: отложив на прямой последовательно стороны одного из этих многоугольников, получим отрезок, равный сумме сторон многоугольника, т. е. получим его периметр. Станем откладывать по прямой AD выпрямленные периметры наших многоугольников от точки A в определенном направлении.
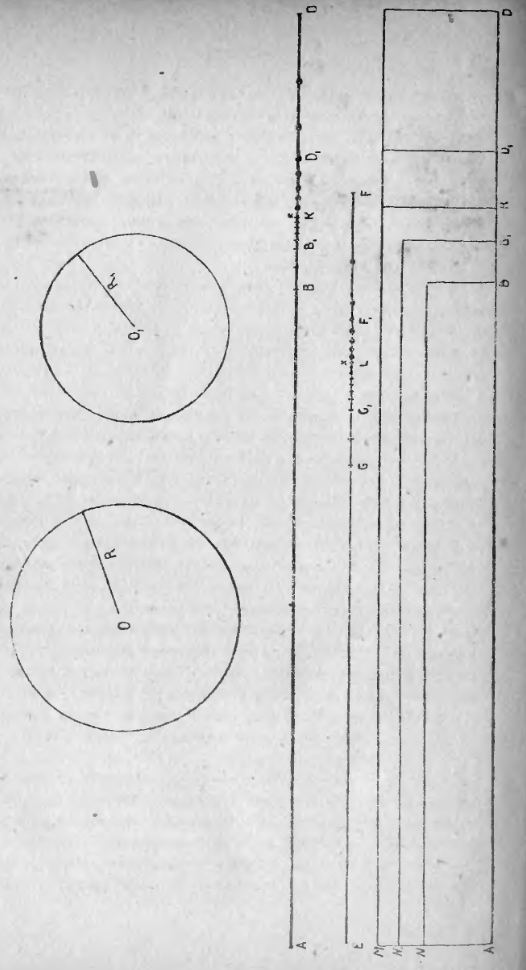
Концы этих периметров дадут на нашей прямой ряд точек, причем концы периметров вписанных многоугольников составят один класс точек, а концы периметров описанных — другой класс. Точки первого класса (на чертеже названы 2 из них буквами B и B1, а другие намечены черточками) не могут попасть в ту область, где расположены точки второго класса (на чертеже две из них названы буквами D и D1, а несколько других намечены кружочками) и обратно: точки второго класса не могут попасть в область, занятую точками первого класса. Справедливость этого ясна из того, что мы знаем, что периметр всякого вписанного в круг многоугольника меньше периметра любого описанного около того же круга многоугольника.
Однако, увеличивая число сторон вписанного многоугольника, мы можем получать точки первого класса, постепенно приближающиеся к точками второго класса, и, увеличивая число сторон описанного многоугольника, мы можем получать точки второго класса, постепенно приближающиеся к точкам первого класса (например, если станем строить правильные многоугольники с постепенно удваивающимся числом сторон, то периметры вписанных многоугольников все увеличиваются, а периметры описанных все уменьшаются, – см. п. 274, пункт 1). Мы знаем еще (п. 274 пункт 5), что можно вписать в круг и описать около него два таких многоугольника, что разность между их периметрами может быть сделана меньше любого отрезка, сколь бы мал он ни был. Поэтому мы можем получить две таких точки, одну в первом классе, а другую во втором, что расстояние между ними меньше любого малого отрезка. Отсюда вытекает, что точки наших двух классов стремятся неопределенно сблизиться между собою.
Если мы обратимся к наглядному представлению расположения точек обоих классов на прямой AD, то мы должны признать, что существует граница, точка K, например, отделяющая область точек I класса от области точек II класса. Этой граничной точке K соответствует отрезок AK, который больше периметра любого вписанного многоугольника и меньше периметра любого описанного многоугольника.
Если бы могли, начав с какого-либо правильного вписанного многоугольника, продолжать процесс удваивания числа сторон без конца, то мы могли бы признать отрезок AK за периметр правильного вписанного многоугольника с бесконечно большим числом сторон. Так же его можно было бы признать и за периметр правильного описанного многоугольника с бесконечно большим числом. Тогда пришлось бы признать, что и сам вписанный многоугольник с бесконечно большим числом сторон совпадает с описанным таким же многоугольником. Но окружность всегда располагается между вписанным и описанным многоугольниками, - пришлось бы признать, что правильный вписанный или описанный многоугольник с бесконечно большим числом сторон совпадает с окружностью, и тогда отрезок AK представлял бы собою выпрямленный периметр круга или, что тоже самое, длину круга.
Итак, мы пришли к необходимость, если желаем решать задачу о выпрямлении круга, рассматривать круг, как правильный многоугольник с бесконечно-большим числом сторон.
276. Воззрение на круг, как на прямоугольник с бесконечно-большим числом сторон, может быть выяснено иным путем:
Чем больше сторон у правильного многоугольника, тем больше и вершин, причем все его вершины находятся на одинаковом расстоянии от центра. У правильного многоугольника с бесконечно большим числом сторон бесконечно много и вершин и все они расположены на одинаковом расстоянии от центра. Мы можем построить совокупность всех точек плоскости, находящихся на одинаковом расстоянии от центра; эта совокупность представляет собою круг. Поэтому мы можем, если это соответствует определенной цели, признать круг за правильный многоугольник с бесконечно большим числом вершин (каждая точка круга может быть рассматриваема, как одна из вершин этого правильного многоугольника) или с бесконечно большим числом сторон.
277. Признав возможным рассматривать круг, как правильный многоугольник с бесконечно-большим числом сторон, мы этим самым признаем, что на круг можно распространить некоторые свойства правильных многоугольников, а именно те, какие имеют место при любом числе сторон. Мы знаем (п. 248), что отношение периметров двух правильных одноименных многоугольников равно отношению их радиусов. Это свойство может быть распространено и на два круга: мы можем признать, что два круга можно рассматривать, как правильные многоугольники, хотя и с бесконечно-большим, но с одинаковым числом сторон (например, мы можем вписать в наши два круга правильные шестиугольники, потом 12-угольники, потом 24-угольники и т. д. без конца, - всякий раз будем получать правильные многоугольники с одинаковым числом сторон); к тому же придем и из следующих соображений: расположим наши два круга I и II так, чтобы они имели общий центр O (чер. 272); тогда каждую точку (напр., A) большого круга следует считать за вершину соответствующего правильного многоугольника с бесконечно большим числом сторон, а ей соответствует единственная точка A' малого круга, лежащая на радиусе OA, и обратно, каждой точке B' малого круга соответствует единственная точка B большого, лежащая на продолженном радиусе OB', т. е. каждой вершине I правильного многоугольника с бесконечно-большим числом сторон — круг I мы рассматриваем, как правильный многоугольник с бесконечно-большим числом сторон — соответствует единственная вершина II правильного многоугольника с бесконечно-большим числом сторон — круг II мы признаем за правильный многоугольник с бесконечно-большим числом сторон — и обратно, каждой вершине II правильного многоугольника соответствует единственная вершина I правильного многоугольника; эти соображения позволяют считать число вершин, а след. и сторон, у обоих правильных многоугольников одинаковым.
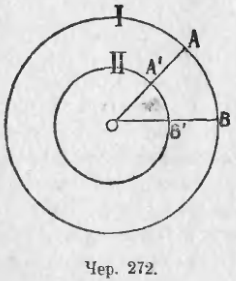
В п. 273 мы признали, что владеем представлением о длине кривой вообще и о длине круга в частности. Назовем радиусы двух кругов через R и R1, а отрезки, которые мы признаем длиною каждого из этих кругов, через C и C1. Тогда мы можем смотреть на отрезки C и C1, как на выпрямленные периметры правильных одноименных многоугольников с бесконечно-большим числом сторон (можно было бы назвать эти отрезки периметрами наших кругов, но так называть не принято). Поэтому мы можем к отрезкам C и C1 применить вышеуказанное свойство одноименных прав. многоугольников, т. е. мы имеем:
C/C1 = R/R1.
Но ясно, что R/R1 = 2R/2R1; поэтому
C/C1 = 2R/2R1,
т. е. отношение длин двух кругов равно отношению диаметров этих кругов.
Применим сюда возможность переставлять средние члены пропорции (п. 178); получим
C/2R = C1/2R1,
т. е. отношение длины круга к его диаметру равно постоянному числу (отношение длины одного круга к своему диаметру равно отношению длины другого круга к своему диаметру и, следовательно, равно отношению длины третьего круга к своему диаметру и т. д.). Это постоянное число можно, как скоро увидим, вычислить с какою-либо точностью, но безошибочно выразить его никакими долями единицы нельзя; его принято обозначать греческой буквой π (пи). Тогда имеем:
C/2R = π,
откуда
C = 2πR.
Эта формула позволяет вычислить длину окружности с какою-либо степенью точности: π, как сказано, мы вычислим с известною степенью точности, R мы можем измерять непосредственно.
Вот еще другие соображения, при помощи которых можно прийти к пропорции C/C1 = R/R1 (а отсюда получить, что C/2R = C1/2R1). Обратимся к чертежу стран. 284. Пусть имеем два круга, радиусы которых R и R1. Станем вписывать в эти круги подобные многоугольники, а также станем около них описывать подобные многоугольники (среди них правильные единоименные); станем затем, как уже это делали, на прямой AD от точки A откладывать выпрямленные периметры многоугольников, вписанных в первый круг и описанных около него, и на прямой EF от точки E — периметры многоугольников вписанных во второй круг и описанных около него. Получим, как уже это было выяснено, на прямой AD два класса точек: 1) точки B, B1 ..., служащие концами периметров многоугольников, вписанных в первый круг и 2) точки D, D1 ..., служащие концами периметров многоугольников, описанных около первого круга, границею между этими классами точек служит точка K; тогда мы признали, что AK есть длина первого круга. Также на прямой EF получим два класса точек: 1) точки G, G1 ..., служащие концами периметров многоугольников, вписанных во второй круг, и 2) точки F, F1 …, служащие концами периметров многоугольников, описанных около второго круга; границею между этими двумя классами точек пусть служит точка L, тогда отрезок EL представляет длину второго круга. Пусть AB и EG суть периметры двух подобных многоугольников (напр., двух правильных одноименных), вписанных в наши два круга; пусть таковыми же еще являются отрезки AB1 и EG1 и т. д., - таких пар отрезков можно получить сколько угодно много.
Пусть также пары отрезков (AD и EF), (AD1 и EF1) и т. д. представляют периметры подобных многоугольников (напр., правильных одноименных), описанных около наших кругов.
Тогда мы имеем:
AB/EG = R/R1, AB1/EG1 = R/R1 …, AD/EF = R/R1, AD1/EF1 = R/R1 …
Мы можем получить сколь угодно много таких пропорций для точек на прямых AD и EF, принадлежащих или к первым классам или ко вторым классам. Если бы мы, увеличивая число сторон вписанных или описанных многоугольников, достигли бы точке K (для первого круга) и L (для второго круга), т. е., если бы получили периметры правильных многоугольников с бесконечно большим числом сторон, радиусы которых суть R и R1, то и для отрезков AK и EL должны были бы признать справедливость пропорции
AK/EL = R/R1,
или, называя AK через C (длина первого круга) и EL через C1 (длина второго круга):
C/C1 = R/R1.
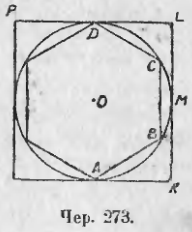
278. В пп. 240-247 мы нашли два простейших правильных многоугольника, один вписанный в круг и другой — описанный около него, стороны которых выражаются рационально чрез радиус круга. Это вписанный правильный шестиугольник: a6 = R и описанный правильный четырехугольник: b4 = 2R. Построим их для круга O (чер. 273). Тогда периметр вписанного шестиугольника меньше длины круга и периметр описанного 4-угольника больше длины круга (Справедливость этого ясна: мы рассматриваем круг, как правильный многоугольник с бесконечно-большим числом сторон, что позволяет применить сюда п. 274, пункт 2. То же заключение вытекает из рассмотрения чертежа на стран. 284, где длина круга есть отрезок AK.), но периметр первого = 6R, а периметр второго = 8R. Следовательно, имеем:
C > 6R и C < 8R.
Заменяя C чрез 2πR, получим:
2πR > 6R и 2πR < 8R,
откуда, после сокращений:
π > 3 и π < 4,
т. е. число π заключается между целыми числами 3 и 4. Таким образом мы вычислили число π с точностью до единицы.
Отсюда видим, как можно было бы вычислить это число с большей точностью: надо рассмотреть периметры вписанных и описанных правильных многоугольников с большим числом сторон, причем для удобства вычисления берут обыкновенно вписанный и описанный многоугольники одноименные. Например, сначала вписанные и описанные 6-угольники, потом 12-угольники, 24-угольники и т. д., все удваивая число сторон. Например, периметр вписанного 48-угольника = 6,279...R, а описанного 48-угольника = 6,292...R.
Отсюда 2πR > 6,279...R и 2πR < 6,292...R,
или π > 3,139... и π < 3,146...
Видим, что у этих двух чисел целые единицы и десятые доли одинаковы, а разница лишь в сотых и т. д. долях.
Очевидно: 3,146 – 3,139 < 0,1. Поэтому, взяв π = 3,1... мы говорим, что целые единицы и десятые доли у нас вычислены верно, сотых и т. д. не знаем и ошибка во всяком случае меньше 0,1.
Существуют и другие способы, более удобные для вычисления π.
Впервые число π было вычислено (с ошибкою меньшею, чем 0,002, Архимедом. Он дал для него π = (приближено) 22/7 = 3(1/7).
Затем в XVI столетии Адриан Меций дал более точное число для π:
π = (приблизительно) 355/113.
(Это число удобно запомнить: написать 3 нечетных первых числа, повторяя каждое два раза 113355 и разделить по середине на 2 группы 113 | 355, – вторая группа есть числитель, а первая знаменатель выше данного числа).
Теперь исключительно выражают π десятичною дробью. Вот значение π ограниченное десятью десятичными знаками:
π = 3,1415926535...
В задачах приходится брать чаще всего π = 3,14 или π = 3,14159 или одно из выше данных чисел (22/7 и 355/113).
Полезно также знать число, обратное π:
1/π = 0,31831...
279. Мы можем вычислять длину круга с какою угодно точностью. Например, пусть радиус круга = 65 лин. един. и желаем вычислить длину круга с точностью до 0,01 лин. един. Для этого надо число π взять с 4 десятичными знаками, т. е. π = 3,1416; последнюю цифру пишем 6, а не 5, так как следующая цифра (первая из отбрасываемых) есть 9. Легко сообразить, что мы делаем для π ошибку меньшую, чем 1/100000. Для вычисления длины круга над это значение π умножить на 2R, т. е. на 136; от этого и ошибка увеличится в 136 раз и окажется меньше 136/100000 или < 1/500. Полученный результат окажется точнее, чем нам требовалось.
280. Мы можем также вычислить длину дуги, содержащей известное число градусов.
Пусть в дуге n°. Назовем ее длину через S. Узнаем сначала длину дуги в 1°: длина всего круга = 2πR, а во всем круге 360°, следовательно,
дл. ◡1° = 2πR/360,
но в нашей дуге n°, следовательно,
S = 2πRn/360 = πRn/180.
Подобным же образом следует поступать, если дуга выражена не только в градусах, но и в минутах и секундах.
Задача. Сколько градусов в дуге, длина которой равна ее радиусу?
Называя искомое число градусов через x и заменяя в предыдущей формуле n через x, а S, согласно условию, чрез R, получим уравнение:
R = πRx/180,
откуда
x = (180/π)° = 180° · 1/π = 180° · 0,3183... = 57° 17' 45'' (приблиз.).
Найденная дуга принимается в высшей математике за единицу при измерении дуг, и она называется радианом.
281. В п. 203 мы узнали, как измерять площадь правильного многоугольника: надо измерить его периметр и апофему и взять половину произведения полученных от их измерения чисел. Применяя это к кругу (круг рассматриваем, как правильный многоугольник с бесконечно-большим числом сторон) и называя площадь, ограниченную кругом чрез K, получим:
K = C · p / 2,
где C (периметр круга) = 2πR, а p — его апофема, она должна считаться равною радиусу круга. Поэтому имеем:
K = 2πR · R / 2 = πR2.
Возможно прийти к тому же результату с иной точки зрения. Обратимся к чертежу на стран. 284. Здесь отрезки AB, AB1 …, AD, AD1 … служат периметрами каких-либо вписанных и описанных многоугольников. Мы можем для каждого из этих многоугольников построить равновеликий ему прямоугольник с определенным основанием. Остановимся лишь на правильных многоугольниках; для каждого из них можно построить равновеликий ему прямоугольник (п. 203), основанием которого служит периметр этого правильного многоугольника, и высотою половина его апофемы (а для описанного около круга правильного многоугольника высота равна половине радиуса этого круга). На стран. 284 построены такие прямоугольники: AB, AB1 … суть периметры правильных вписанных многоугольников (На чертеже половины апофем AN, AN1 … ½ радиуса (AM) даны в увеличенном виде.), AD, AD1, … - периметры правильных описанных многоугольников, AM — половина радиуса круга (AM есть общая высота прямоугольников, равновеликих правильным описанным многоугольникам).
Так как периметр любого вписанного многоугольника меньше периметра любого описанного и апофема вписанного правильного многоугольника меньше радиуса круга, то прямоугольники, равновеликие вписанным многоугольникам, заключены внутри любого из прямоугольников, равновеликих описанным многоугольникам. Так как концы периметров вписанных многоугольников (точки B, B1, …) приближаются как угодно близко к точкам D, D1, …, служащих концами выпрямленных описанных многоугольников (п. 274, пункт 5), так как, кроме того, апофемы правильных вписанных многоугольников могут быть сделаны (увеличением числа сторон многоугольника) сколь угодно близкими к радиусу круга (п. 274 пункт 4), то площади наших прямоугольников ABN, AB1N1, … стремятся, с увеличением числа сторон у многоугольников, неопределенно сблизиться с площадями прямоугольников ADM, AD1M, … Границею между этими двумя классами прямоугольников является прямоугольник AKM, основание которого отрезок AK представляет длину нашего круга. Площадь этого прямоугольника мы уже должны признать равной площади круга, так как площадь прямоугольника AKM больше площади любого из прямоугольников первого класса (ABN, AB1N1 …) и меньше площади любого из прямоугольников второго класса (ADM, AD1M, …), а таким же свойством, как мы непосредственно видим, обладает площадь круга: она больше площади любого вписанного в этот круг многоугольника. Называя через C число, выражающее длину нашего круга (т. е. отрезок AK) в каких-либо линейных единицах, и через R — число, выражающее радиус круга в тех же линейных единицах, мы найдем, что площадь прямоугольника AMK или площадь круга = C · R/2 (ибо AM = ½R), или K = 2πR · R / 2 = πR2.
282. Построим для круга O (чер. 274) два радиуса OA и OB. Фигура, состоящая из этих двух радиусов и дуги AB, заключенной между ними, называется круговым сектором (иногда просто называют сектор). Мы можем вычислить площадь, ограниченную сектором, если знаем, сколько градусов в его угле AOB. Положим, что ∠AOB = n°. Тогда имеем: площадь круга = πR2, площадь сектора в 1° = πR2/360, потому что можно построить 360 секторов, площади которых равны между собою и вместе составляют площадь круга, – угол такого сектора = 1°, а площадь сектора в n° = πR2 · n / 360. Называя эту площадь через Q имеем:
Q = πR2 · n / 360.
Можно эту формулу переделать:
Q = (πRn/180) · R/2 = sR/2,
где чрез s обозначена длина ◡AB (в п. 280 мы получили, что s = πRn/180).
Полученную формулу выражают словами: площадь сектора равна половине произведения длины его дуги на радиус.
В задачах чаще приходится пользоваться первою формулою.
Если построим хорду CD (чер. 274) и рассмотрим фигуру, состоящую из хорды CD и ◡CD, то она называется круговым сегментом (иногда называют просто сегмент). Чтобы измерить площадь, ограниченную сегментом CDM, надо измерить площадь сектора COD и площадь треугольника COD, затем из первой вычесть вторую.
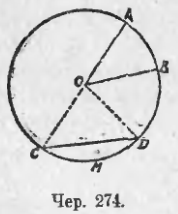
283. Упражнения.
1. Каков должен быть радиус круга, чтобы его длина равнялась 10 дм.?
2. На радиусе OA круга построим, как на диаметре, другой круг. Затем построим еще радиус первого круга, пересекающий второй круг в точке B и первый в точке C. Тогда длина дуги AB равна длине дуги AC.
3. Сумма стороны правильного треугольника и стороны квадрата вписанных в круг равна приблизительно (с точностью до 0,01) половине длины этого круга.
4. Длина дуги в 20° равна 1(1/9)π дм. Найти длину дуги в 36° другого круга, радиус которого на 2 дм больше радиуса первого. (Ответ: 2,4π дм.)
5. На сколько надо увеличить радиус круга, чтобы длина его дуги в 24° увеличилась на π/2 дм. (Ответ: на 3(3/4) дм.)
6. Радиус круга = 6 лин. един. Вычислить площадь сегмента, дуга которого содержит 120°. (Ответ: (12π – 9√3) кв. един.)
7. Вычислить площадь правильного четырехугольника, вписанного в круг, если площадь сектора этого круга с углом 20° равна 8π кв. един.
8. Построены три концентрических круга: радиус второго равен стороне правильного четырехугольника, вписанного в первый, а радиус третьего равен стороне правильного треугольника, вписанного во второй. Найти отношение площадей двух колец между этими кругами. (Ответ: ¼.)
9. Найти площадь кольца, ограниченного двумя концентрическими кругами, если длина дуги в 20° первого круга = 2π лин. един. и длина дуги в 18° второго круга = также 2π лин. един. (Ответ: 76π кв. един.)
10. Из точки круга, радиус которого = R, построены две хорды: одна из них равна радиусу, а другая — стороне квадрата, вписанного в этот круг, и обе они расположены по одну сторону центра. Вычислить площадь, ограниченную двумя построенными хордами и дугою между ними. (Ответ: (R2/12)(π + 3√3 – 6).)
11. Построен равносторонний треугольник и на его стороне, как на диаметре, построен круг. Вычислить ту часть площади треугольника, которая лежит вне круга, если сторона треугольника = a. (Ответ: (a2/24)(3√3 – π).)
12. Построен квадрат, сторона которого = a. Затем построен круг, центр которого расположен в середине одной стороны квадрата и который проходит чрез середины двух других его сторон. Вычислить ту часть площади квадрата, которая расположена вне круга. (Ответ: a2/16(12 – π).)
13. Основание равнобедренного треугольника = 2a, а его боковая сторона = b. Вычислить площадь круга, вписанного в этот треугольник. (Ответ: a2(b – a) / (b + a).)
14. Сколько градусов, минут и секунд в угле сектора, равновеликого квадрату, стороною которого служит выпрямленная дуга этого сектора?
