89. Пусть даны 2 точки A и B (чер. 99). Мы можем построить: 1) прямолинейный отрезок AB, концы которого совпадают с данными точками; 2) несколько линий, из которых каждая соединяет точки A и B и состоит из ряда прямолинейных отрезков, напр., ACDEFB или AKLMB, – такие линии называют ломаными и 3) ряд кривых линий, соединяющих точки A и B, напр., ANB (мы умеем строить из кривых линий только одну — дугу круга, но возможно вообразить, что через точки A и B проходит множество и иных каких-либо кривых линий, отличающихся по форме от дуги круга). Возникает вопрос о сравнении между собою всех этих линий.
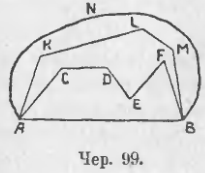
Прежде чем обратиться к рассмотрению этого вопроса, обратим внимание на два различных вида ломаных линий, причем мы ограничимся тем случаем, когда ломаная располагается только по одну сторону прямой AB, продолженной в обе стороны: ломаная AKLMB вместе с отрезком AB составляют многоугольник, имеющий площадь, все внутренние углы которого меньше выпрямленного, – такой многоугольник называется, как мы знаем, выпуклым; поэтому и сама ломаная AKLMB называется выпуклою ломаною, а ломаная ACDEFB вместе с отрезком AB составляет многоугольник, имеющий площадь, один из внутренних углов которого (при точке E) больше выпрямленного, – такой многоугольник, как знаем, не выпуклый; поэтому и сама ломаная ACDEFB не выпуклая.
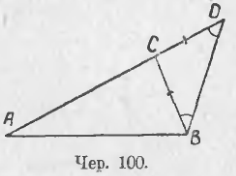
90. Приступая к решению намеченного вопроса, сравним сначала отрезок AB, соединяющий точки A и B (чер. 100), с простейшей ломаною ACB, состоящею только из двух прямолинейных отрезков AC и CB. Для выполнения этого сравнения надо ломаную ACB выпрямить, т. е. Расположить отрезки AC и BC на одной прямой, приложенными друг к другу, или сложить отрезки AC и CB (п. 9). Для этого продолжим отрезок AC и на его продолжение отложим отрезок CD = CB. Тогда AD = AC + CD или AD = AC + CB. Построив отрезок BD, получим равнобедренный ∆BCD (CD = CB), у которого углы при основании равны, т. е. ∠CBD = ∠CDB. Рассматривая затем ∆ABD, видим, что ∠ABD > ∠CBD, а, следовательно, ∠ABD > ∠CDB (ибо ∠CDB = ∠CBD). На основании п. 86 имеем поэтому AD > AB (против большего угла в треугольнике лежит и большая сторона), или AC + CB > AB, т. е. Ломаная ACB больше отрезка AB.
Этот результат удобно выразить в следующей форме: После построения отрезка AB и ломанной ACB, мы получили ∆ACB, и тогда сумма AC + CB есть сумма двух его сторон, причем у нас оказалось, что AB < AC + CB, т. е.
Одна сторона треугольника меньше суммы двух других его сторон.
91. Здесь можно получить еще соотношение между сторонами треугольника. Мы нашли для ∆ACB (чер. 100)
AC + CB > AB.
Воспользуемся следующим очевидным для нас соображением: если одно число больше другого и если мы вычтем их них поровну, то первая разность останется больше второй; также, если один отрезок больше второго и если мы из них вычтем (п. 10) одинаковые отрезки, то первая разность останется больше второй. Заметим, что AC + CB мы рассматриваем, как один отрезок, так как мы умеем складывать два отрезка. Вычтем из большого отрезка (AC + CB) и из меньшего AB По одинаковому отрезку, а именно по отрезку CB; тогда получим, согласно выше изложенному соображению,
AC > AB – CB,
т. е. одна сторона треугольника больше разности двух других.
Найденные в пп. 90 и 91 соотношения между сторонами треугольника те же самые, которые были указаны в п. 38.
92. Построим теперь через точки A и B отрезок AB и выпуклую ломаную AKLMB (чер. 101), состоящую из скольких угодно отрезков. Требуется сравнить ломаную AKLMB с отрезком AB.
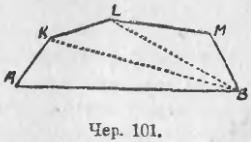
Чтобы воспользоваться предыдущим, построим вспомогательный отрезок BK, тогда из ∆AKB:
AB < AK + KB.
Построив еще отрезок LB, найдем из ∆KLB:
KB < KL + LB.
И, наконец, из ∆LMB получим:
LB < LM + MB.
Воспользуемся соображением: если каждый из нескольких отрезков меньше каких-либо других отрезков, то и сумма меньших отрезков меньше суммы больших. Применяя это к нашим отрезкам, имеем:
AB + KB + LB < AK + KB + KL + LB + LM + MB.
Вычтя из обеих сумм одинаковые отрезки (KB и LB), найдем:
AB < AK + KL + LM + MB,
т. е. прямолинейный отрезок, соединяющий две точки, меньше всякой выпуклой ломаной, соединяющей те же точки.
Ясно, что это свойство применимо и к выпуклой ломаной; напр., если имеем ломаную ACDEFB (чер. 99), то, построив отрезок DF получим ломаную ACDFB, которая больше отрезка AB, а замена отрезка DF суммою DE + EF еще увеличит эту ломаную (п. 90).
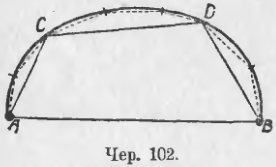
93. Пусть построена какая-либо кривая ACB (чер. 102), соединяющая точки A и B. Выпрямлять ее, как выпрямляли в п. 90 ломаную, мы не умеем, и поэтому приходится довольствоваться здесь косвенными соображениями. Возьмем на кривой какие-либо точки C и D и соединим их с A и B и между собою отрезками, получим ломаную ACDB; если на частях кривой AC, CD, DB возьмем какие-либо еще промежуточные точки и построим ломаную, то, при достаточном числе этих промежуточных точек, отрезки новой ломаной могут быть сделаны меньше отрезков первой ломаной. Мы можем этот процесс продолжить дальше, – тогда будут получаться ломаные линии, имеющие все больше и больше вершин, которые все располагаются на нашей кривой, а стороны или отрезки этих ломаных все уменьшаются. Возможность продолжать такое построение ломаных сколь угодно далеко позволяет нам признать, что возможно кривую линию рассматривать, как ломаную, составленную из бесконечно большого числа бесконечно малых отрезков. Поэтому мы в праве применить свойство п. 92 ломаной и к кривой, и тогда будем иметь, что отрезок AB надо считать меньшим, чем кривая ACB.
В виду найденных соотношений между различными линиями, соединяющими две точки, мы установим:
Под словами: расстоянием между двумя точками понимают: прямолинейных отрезок, соединяющий эти две точки.
94. Сравним затем две выпуклые ломаных линии, соединяющих две точки и расположенных по одну сторону прямой, соединяющей эти две точки, причем одна из них охватывает (объемлет) другую.
Пусть эти ломаные суть ACDB (чер. 103) — объемлемая и AMNPB — объемлющая.
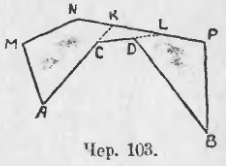
Для их сравнения продолжим отрезки AC и CD до пересечения где-либо с отрезками объемлющей ломаной в точках K и L.
Тогда на основании пп. 90 и 92 имеем:
1) AC + CK < AM + MN + NK.
2) CD + DL < CK + KL.
3) BD < DL + LP + PB.
Взяв сумму меньших частей этих неравенств и сумму их больших частей, получим:
AC + CK + CD + DL + BD < AM + MN + NK + CK + KL + DL + LP + PB
Вычтем одинаковые отрезки CK и DL, – тогда:
AC + CD + BD < AM + MN + NK + KL + LP + PB
Или заменяя NK + KL + LP через NP, получим:
AC + CD + BD < AM + MN + NP + PB,
т. е. выпуклая объемлемая ломаная, соединяющая две точки, меньше объемлющей, соединяющей те же точки.
Заметим: 1) это свойство имеет силу и для кривых линий (кривую линию мы называем выпуклою, если ломаные линии, получаемые от соединения отрезками сколь угодно часто расположенных точек на этой кривой, - все оказываются выпуклыми).
2) Объемлющая линия может быть и невыпуклой.
95. Упражнения.
I. Прямая, соединяющая вершину треугольника с серединою противоположной стороны, называется медианою этого треугольника. Всего в треугольнике можно построить три медианы, - все они, как это выяснится впоследствии, пересекаются в одной точке.
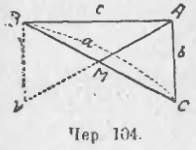
Пусть имеем ABC и AM его медиана (чер. 104) (M середина BC). Назовем для краткости сторону BC через a (против ∠A), сторону CA через b, сторону AB через c, медиану AM через m1, медиану, идущую из точки B к средине стороны AC, через m2 и третью медиану из точки C чрез m3.
Выяснить следующее свойство медиан:
1) m1 < (b + c) / 2 (надо сделать следующее построение: продолжить AM и чрез построить BN || AC – рассмотреть ∆ABN);
2) m1 > (b + c – a) / 2;
3) m1 + m2 + m3 < a + b + c. Сума сторон треугольника называется периметром этого треугольника; поэтому это свойство выражают словами: сумма медиан треугольника меньше го периметра;
4) m1 + m2 + m3 > (a + b + c) / 2 (выразить словами).
II. Возьмем внутри треугольника какую-либо точку O (на чертеже не дана) и назовем OA чрез r1, OB чрез r2 и OC чрез r3. Тогда имеют место зависимости:
1) r1 + r2 + r3 > (a + b + c) / 2 и 2) r1 + r2 + r3 < a + b + c.
III. Распространить последние свойства на точку, взятую внутри выпуклого четырехугольника [r1 + r2 + r3 + r4 > (a + b + c + d) / 2, но r1 + r2 + r3 + r4 < 1½ (a + b + c + d)].
96. Пользуясь понятием о расстоянии между двумя точками, мы теперь можем установить на основании изложенного в п. 20:
Все точки плоскости, находящиеся на данном расстоянии от данной точки, расположены на круге, центр которого – данная точка, и радиус равен данному расстоянию. Обратно, каждая точка нашего круга находится на данном расстоянии от данной точки (от центра).
Геометрическое место точек (плоскости), находящихся на данном расстоянии от данной точки, есть круг, центром которого служит данная точка и радиус которого равен данному расстоянию.
Иногда говорят: круг есть геометрическое место точек, равноотстоящих от данной точки (от центра).
97. Задача. Даны две точки. Построить перпендикуляр к отрезку, соединяющему эти две точки чрез его середину.
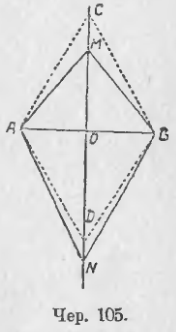
Пусть A и B (чер. 105) – данные точки. Задача легко решается построением ромба ACBD, у которого две вершины суть A и B и одна диагональ есть отрезок AB. Как строить такой ромб, было уже выяснено выше. Вторая диагональ CD этого ромба проходит через точку O, середину отрезка AB, и перпендикулярна к AB.
Рассмотрим расстояния какой-либо точки M перпендикуляра CD от точек A и B. Соединив M с A и B, получим ∆AOM и ∆MOB, которые между собою равны (они прямоугольные и катеты одного равны соответственно катетам другого: OM общий катет и OA = OB). Отсюда заключаем, что MA = MB. Можно взять точку где-либо на продолжении прямой CD, например, точку N; также найдем, что NA = NB.
Это свойство точек построенного перпендикуляра можно выразить в следующей форме:
Всякая точка перпендикуляра, построенного к отрезку, соединяющему две данные точки, чрез середину этого отрезка, отстоит на равных расстояниях от двух данных точек (короче: равноудалена от данных точек).
Возможно ли где-либо на плоскости, не на перпендикуляре CD, найти точку, равноудаленную от A и B?
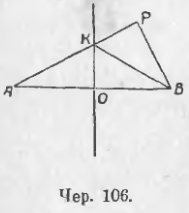
Возьмем где-либо не на перпендикуляре CD точку P (чер. 106) и рассмотрим ее расстояния от точек A и B, т. е. отрезки PA и BP. Один из этих отрезков, например, PA, пересекает наш перпендикуляр CD в точке K. Тогда, соединив K и B, найдем по предыдущему
KB + KA,
ибо точка K, будучи расположена на перпендикуляре, одинаково удалена от B и A.
Кроме того, из ∆PKB имеем (п. 90):
PB < PK + KB.
Или, заменяя KB чрез KA (эти отрезки равны), имеем:
PB < PK + KA или PB < PA,
т. е. точка P, взятая не на перпендикуляре CD, неодинаково удалена от точек A и B.
Итак, все точки, равноудаленные от двух данных, непременно должны лежать на перпендикуляре к отрезку, соединяющему данные точки, через его середину; с другой стороны, любая точка этого перпендикуляра обладает этим свойством. Поэтому говорят:
Геометрическое место точек (плоскости), равноудаленных от двух данных точек, есть перпендикуляр к отрезку, соединяющему данные точки, проходящий через его середину.
98. Упражнения. 1. Найти на данной прямой или на данной окружности точку, равноудаленную от двух данных.
2. Найти точку, равноудаленную от трех данных точек. Когда такой точки не существует?
