99. Пусть дана прямая a и точка A вне ее (чер. 107). Мы можем построить AB ⊥ a и знаем (п. 70), что другого перпендикуляра через A к прямой a построить нельзя; если мы построим ряд прямых, идущих из A к различным точкам данной прямой a: AC, AD, AE и т. д., то мы будем называть их наклонными к прямой a. Точки B, C, D, E называют основаниями перпендикуляра AB, наклонных AC, AD, AE.
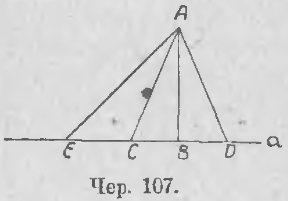
Из ∆ABC, например, видим, что AB < AC, так как ∠B в этом треугольнике прямой, а ∠C острый (п. 72), а против большего угла лежит и большая сторона (п. 86); то есть оказывается, что перпендикуляр AB меньше любой наклонной AC.
Пусть построены две наклонных AC и AD так, чтобы их основания C и D были одинаково удалены от основания перпендикуляра, т. е., чтобы BC = BD. Тогда ∆ABC = ∆ABD (у них катет AB общий и катет BC = BD), следовательно, AC = AD, т. е. две наклонные, основания которых одинаково удалены от основания перпендикуляра, равны между собою.
Построим еще наклонную AE, основание которой E дальше отстоит от основания перпендикуляра, чем основание наклонной AC, т. е. BE > BC. Тогда ∠ACE тупой, так как этот угол есть внешний для ∆ACB и, следовательно, он больше прямого угла B; отсюда, рассматривая тупоугольный треугольник ACE, видим (п. 72), что ∠E острый и опять на основании п. 86 заключаем, что AE > AC или AE > AD (ибо AD = AC), т. е., если основание одной наклонной дальше отстоит от основания перпендикуляра, чем другой, то первая наклонная больше второй.
Для того, чтобы выразить найденные свойства в более простой словесной форме, станем называть отрезок BC проекциею наклонной AC, BD — проекциею наклонной AD, BE — проекциею наклонной AE и т. д. Тогда:
Если дана прямая и вне ее точка и через эту точку построены перпендикуляр и наклонные к прямой, то
1) перпендикуляр меньше всякой наклонной;
2) две наклонные с равными проекциями равны;
3) из двух наклонных с неравными проекциями та больше, у которой проекция больше.
Обратно:
1) проекция равных наклонных равны между собою;
2) та из двух неравных наклонных имеет большую проекцию, которая сама больше.
Выяснить справедливость этих заключений можно способом, который был применен в п. 86. Разберем 2-е обратное заключение. Пусть наклонная AE > AD; об их проекциях BE и BD можно сделать 3 предположения: 1) BE < BD, 2) BE = BD и 3) BE > BD. Легко видеть, что первое и второе предположения не годятся; следовательно, 3-е предположение должно быть справедливым. Первое обратное заключение можно получить или этим же способом, или увидать его из рассмотрения ∆ABC и ∆ABD.
В виду найденного свойства перпендикуляра принимают за расстояние точки от прямой отрезок перпендикуляра, опущенного из этой точки на прямую.
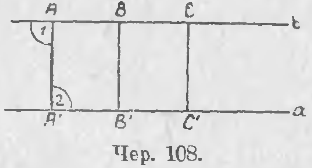
100. Пусть имеем две параллельных прямых a и b (чер. 108). Выберем на прямой b ряд точек A, B, C и т. д. Мы уже знаем, что за расстояние каждой из них от прямой a принимаются перпендикуляры AA', BB', CC' …, построенные чрез точки A, B, C... к прямой a. Легко увидать: 1) Если a ∥ b и если AA' ⊥ a, то AA' ⊥ b, так как, напр., ∠1 = ∠2 (как внутренние накрест-лежащие при параллельных a и b и секущей AA') и, следовательно, ∠1 = d (ибо ∠2 = d), 2) AA' = BB' = CC' и т. д., так как, напр., AA'B'B является параллелограммом (прямоугольником), откуда AA' = BB'. Поэтому отрезок, равный одному из построенных перпендикуляров, принимают за расстояние между двумя параллельными.
101. Где расположены точки, находящиеся на данном расстоянии от данной прямой?
Пусть дана прямая a (чер. 109). Тогда, построив BC ⊥ a и отложив отрезки AB и AC, равные данному расстоянию, получим две точки B и C, расстояние которых от прямой a равно данному. Построив затем прямую BB' || a и CC' || a, увидим, согласно предыдущему, что все точки этих прямых BB' и CC' имеют данное расстояние от прямой a. Все остальные точки, не лежащие на построенных прямых, имеют или меньшее расстояние от прямой a (ближе к a), напр., точка M, или большее (дальше от a), напр., точка N. Поэтому имеем:
Геометрическое место точек, имеющих данное расстояние от данной прямой, есть пара прямых, параллельных данной и расположенных по обе ее стороны на одинаковом (данном) расстоянии.
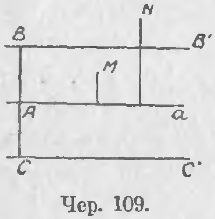
102. Теперь легко увидать, что геометрическим местом точек, равно удаленных от двух данных параллельных прямых, является прямая, параллельная данным и проходящая чрез середину расстояния между ними [напр., прямая a (чер. 109) есть геометрическое место точек, равноудаленных от BB' и CC'].
103. Пусть теперь имеем две пересекающихся прямых AA' и BB' (чер. 110) и пусть точка O есть их общая точка.
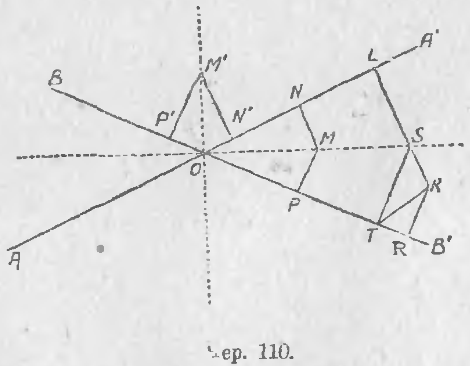
При точке O имеем 4 угла; построим биссекторы этих углов (на чер. они начерчены пунктиром), – эти 4 биссектора составят две взаимно перпендикулярных прямых, что легко увидать. Возьмем на одном из биссекторов какую-либо точку M и построим MN ⊥ AA' и MP ⊥ BB'; тогда MN и MP служат расстояниями точки M от прямых AA' и BB'. Рассматривая ∆OMN и ∆OMP, у которых гипотенуза OM общая – треугольники прямоугольные – и ∠MON = ∠MOP (ибо OM есть биссектор), найдем (п. 74, 3-й признак), что ∆MON = ∆MOP и, следовательно, MN = MP, т. е. точка M одинаково удалена от этих прямых (AA' = BB'); также найдем, что точка M' одинаково удалена от этих прямых (M'P' = M'N'). Если мы рассмотрим точку K, не лежащую на биссекторе OS угла A'OB', то, построив KL ⊥ AA' и KR ⊥ BB', найдем: KL пересекает биссектор в точке S и тогда ST = SL (ST есть ⊥ к BB'), но KR < KT (ибо KR перпендикуляр, а KT — наклонная), а KT < KS + ST (п. 90) или KT < KS + SL или KT < KL; следовательно, и подавно KR < KL, т. е. точка K не расположена на биссекторе, неодинаково удалена от прямых AA' и BB'. Поэтому имеем:
Геометрическим местом точек, равноудаленных от двух данных пересекающихся прямых, служат биссекторы углов, образуемых этими прямыми.
Следовательно, всякая точка, равно удаленная от двух пересекающихся прямых, лежит на биссекторе одного из четырех углов, и, наоборот, всякая точка биссектора одинаково удалена от наших прямых.
104. Пусть имеем круг O и точку A вне его (чер. 111) или внутри его (чер. 112). Тогда, соединив A с O, назовем через B и C точки пересечения прямой AO с кругом; соединяя точку A с различными точками D, E... круга, найдем: 1) для случая, данного на чер. 111, AO < AD + OD или AB + OB < AD + OD, но OB = OD, как радиусы, следов., AB < AD; для случая, данного на чер. 112, имеем: AO > OD – AD или OB – AB > OD – AD, или –AB > –AD, или AB < AD; 2) AD < AO + OD или, заменяя OD через OC (OD = OC), AD < OA + OC, или AD < AC; 3) из рассмотрения ∆AOD и ∆AOE, у которых OA общая сторона и OD = OE (как радиусы), имеем (п. 87) AE > AD, так как ∠AOE > ∠AOD.
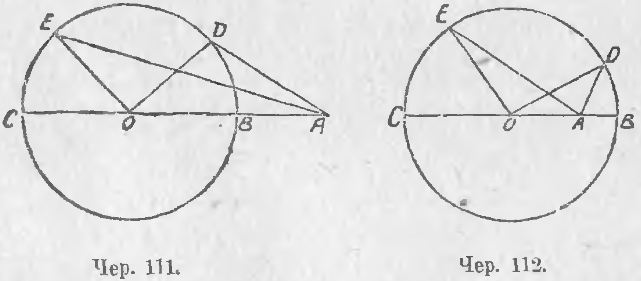
Из этого видим, что если идти по окружности от точки B к точке C, то расстояния точке окружности от точки A будет увеличиваться; наименьшим расстоянием является отрезок AB. Этот последний отрезок принимают за расстояние точки от круга. Итак,
Чтобы получить расстояние точки от круга, надо соединить точку с центром и взять тот отрезок этой прямой между данною точкою и точкою пересечения прямой с кругом, внутри которого не расположен центр.
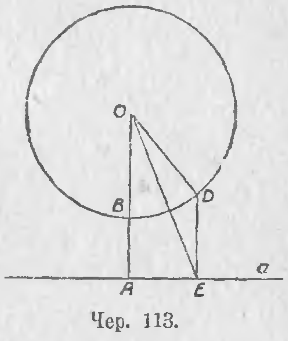
105. Пусть имеем круг O (чер. 113) и какую-либо прямую a, неимеющую общих точек с кругом. Построим через центр круга O перпендикуляр к a, OA ⊥ a и назовем точку пересечения прямой OA с кругом, которая лежит между O и A, через B. Тогда имеем:
AB = OA – OB.
Взяв какую-либо еще точку D круга, построим DE ⊥ a и соединив E с O, найдем из ∆ODE:
DE > OE – OD.
Но OE > OA (наклонная больше перпендикуляра), OB – OD (как радиусы), следов., OE – OD > OA – OB. Поэтому DE > BA.
Отрезок перпендикуляра BA является таким образом расстоянием между двумя наиболее сближенными точками круга и прямой и поэтому его принимают за расстояние между кругом и прямой.
106. Упражнения. 1. Каждая точка основания равнобедренного треугольника обладает свойством, что сумма ее расстояний от равных сторон одна и та же. (Здесь понадобится пользоваться свойством, что 2 высоты равнобедренного треугольника, опущенные на разные стороны, равны между собою).
2. Сумма расстояний каждой точки, расположенной внутри равностороннего треугольника, от всех его сторон есть величина постоянная.
Примечание. Если в первой задаче взять точку на продолжении основания, то разность ее расстояний от равных сторон окажется постоянной; если во второй задаче взять точку вне треугольника, то одно или два из расстояний придется взять со знаками минус.
3. Построим из точки M три луча так, чтобы углы между ними были равны между собою (каждый из них = 4d/3; при построении надо вспомнить задачу 7 из п. 76) и возьмем на них точки A, B и C. Тогда точка M среди всех остальных точек плоскости обладает свойством, что сумма ее расстояний от A, B и C есть наименьшая.
Для выяснения этого надо чрез A, B и C построить прямые соответственно перпендикулярные к MA, MB, MC — получится равносторонний треугольник.
Взяв точку M' (для простоты внутри треугольника), найдем, что сумма ее расстояний от сторон треугольника остается прежней (на основании предыдущей задачи), а, следовательно, сумма ее расстояний от точек A, B и C окажется больше прежней.
4. Геометрическим местом точек, расстояние которых от основания равнобедренного треугольника равно сумме расстояний их от боковых его сторон, служат 2 отрезка, заключенные между равными сторонами треугольника, неопределенно продолженными, прямых, параллельных основанию; точки же этих прямых, не лежащие внутри угла, образованного равными сторонами, обладают свойством, что расстояние их от основания равно разности расстояний от боковых сторон.
Для построения этого геометрического места следует построить биссекторы внутреннего и внешнего углов при основании равнобедренного треугольника.
5. Две вершины треугольника одинаково удалены от прямой, соединяющей третью вершину со срединой противолежащей ей стороны (от медианы).
6. Найти точку, находящуюся на данных расстояниях от данной точки и от данной прямой (наибольшее число решений 4).
7. Даны 2 параллельных прямых, пересеченных секущею. Найти точку, равно удаленную от всех трех прямых (2 решения).
8. Найти точку, равно удаленную от трех прямых, пересекающихся в трех точках (4 решения).
9. Дана прямая и 2 точки A и B, расположенные по одну сторону прямой. Найти на данной прямой такую точку M, чтобы лучи MA и MB были одинаково наклонены к данной прямой. Выяснить, что точка M среди остальных точек данной прямой обладает свойством, что сумма ее расстояний от A до B наименьшая.
10. Найти точку, находящуюся на данных расстояниях от двух данных кругов (предварительно надо выяснить, где расположены точки, находящиеся на данном расстоянии от одного данного круга).
