1. Опыт постоянно сталкивает нас с делением чего-либо на части: разрезая ножом яблоко, мы делим его на части; раскрасив различными красками (например, черной и красной – см. прилагаемый рисунок) взятый кусок белой бумаги, мы этим самым разделим поверхность этого куска бумаги на части: на белую, на черную, на красную; поверхность Европы, мы знаем, разделена на государства; налив в стакан воды, чтобы он не был наполнен, мы этим самым разделим пространство, заключенное внутри стакана, на части: одна наполнена водою, другая – пустая (наполнена воздухом); насыпав в ящик в одну сторону песку, а в другую глины так, чтобы песок и глина не смешались (для чего их удобно намочить), мы разделим пространство, заключенное внутри этого ящика, на части: одна занята песком, другая глиною и третья, если ящик не наполнен, занята воздухом.

Мы признаем, что во всех случаях, подобных перечисленным, существует между двумя соседними частями граница: мы постоянно говорим, рассматривая карту Европы, о границе между Россией и Китаем, между Германией и Францией и т. д.; на прилагаемом раскрашенном рисунке мы видим границу между красною и белою, между черною и белою, между красною и черною частями бумаги; мы также видим границу между частями пространства, заключенными внутри ящика, из которых одна занята песком, другая глиною, третья воздухом.
Для геометрии является существенным вопрос о процессе деления на части и о границах между двумя соседними частями, получаемыми от этого деления. Рассмотрим подробнее процесс деления на части.
Все, что мы видим – мебель в этой комнате, соседние дома, деревья, облака, солнце, луна, звезды, наконец, мы сами – все помещается в пространстве. Определить, что такое пространство, нельзя, но мы из опыта выработали его основные свойства, мы можем представлять в своем воображении эти свойства, можем о них размышлять. Прежде всего нам ясны два свойства пространства: 1) пространство безгранично, и 2) можно вообразить его разделенным на части (опыт постоянно нам говорит о последнем свойстве: всякий предмет, например, наше тело, выделяет из беспредельного пространства некоторую часть, т. е. делит его на части: на часть, занимаемую этим телом, и на все остальное); способность пространства быть разделенным на части выражают иногда словами: пространство имеет протяжение.
Граница между двумя соседними частями пространства называется поверхностью (например, поверхность земли отделяет часть пространства, занимаемую земным шаром от всего остального пространства). Поверхность, в свою очередь, имеет протяжение, т. е. ее можно вообразить разделенною на части (например, поверхность земли разделяют на водную и материковые части; лист бумаги выделяет из пространства часть, занятую веществом бумаги; граница, выделяющая эту часть пространства от остального, есть поверхность этого листа бумаги; она делится на несколько частей: 2 части предназначаются для письма на них, и 4 части, ускользающие благодаря своей незначительности от нашего внимания, – те, по которым обрезан этот лист). Граница между двумя соседними частями поверхности называется линиею (рассмотреть границы между областями различных цветов на данном выше раскрашенном рисунке). Линия, в свою очередь, имеет протяжение, т. е. ее можно вообразить разделенною на части (например, граница, отделяющая на выше данном раскрашенном рисунке). Линия, в свою очередь, имеет протяжение, т. е. ее можно вообразить разделенною на части (например, граница, отделяющая на выше данном раскрашенном рисунке белую часть бумаги от цветной, разделяется на 2 части: одна отделяет белую от красной, другая – белую от черной; граница, отделяющая Германию от остальной Европы, разделяется на части: одна отделяет Германию от Франции, другая – от Австро-Венгрии и т. д.). Граница между двумя соседними частями линии называется точкою. Точку мы уже не можем вообразить разделенной на части, – точка не имеет протяжения.
Из выше данного исследования вопроса о делении на части следует, что мы признаем существование поверхностей, линий и точек, которые все помещаются в пространстве. Раз мы признаем их существование, мы должны выработать способность представлять их, хотя они и невещественны, и рассуждать о них. Цель геометрии состоит в изучении особенностей поверхностей, линий и точек, как отдельно взятых, так и взятых в сочетании друг с другом.
Всякая совокупность поверхностей, линий и точек называется геометрическою фигурою (иногда геометрическим образом или геометрическою формою). Каждая поверхность, каждая линия, каждая точка, входящая в состав фигуры, называется ее частью. Так как всякая фигура помещается в пространстве, то, изучая фигуры, мы тем самым изучаем свойства пространства, причем это изучение состоит в том, что 1) мы устанавливаем, какие фигуры можно осуществить в пространстве, и 2) изучаем особенности этих фигур. Поэтому говорят иногда, что
Геометрия есть наука о пространстве.
2. Мы должны развить способность воображать как бы существующими невещественные геометрические фигуры. Эта способность называется геометрическим представлением. Некоторые свойства фигур мы открываем путем геометрического представления, и иным путем выяснить их невозможно. Такие свойства называются аксиомами. Вот аксиома, общая для всевозможных фигур:
Всякую фигуру можно переносить из одного места пространства в другое, – от этого фигура не претерпевает никаких изменений.
В основе этой аксиомы положена мысль, что пространство однородно.
Таким образом мы можем фигуру переносить в пространстве; если перенесением одной фигуры можно добиться, чтобы она совпала с другою, то такие две фигуры называются равными или конгруэнтными. Итак, равными фигурами называются такие, которые при наложении совпадают всеми частями.
3. При дальнейшем изучении фигур получают ряд свойств, пользуясь, с одной стороны, непосредственным геометрическим представлением, а с другой – рассуждениями, построенными по правилам логики. Такие свойства называются теоремами. Рассуждения, при помощи которых выясняется справедливость теоремы, называют ее доказательством.
Одним из глубоких вопросов является вопрос об отделении того, что узнано вами только непосредственным представлением, и того, чего достигли путем логики. Этот вопрос, несмотря на много работ в этом направлении, нельзя до сих пор считать решенным. В курсе элементарной геометрии и непосредственное геометрическое представление и логика должны взаимно помогать друг другу, чтобы найденное свойство, по возможности, обрисовалось для нас со всех сторон.
Иногда случается, что раз найдена какая-либо теорема, то тотчас же становится ясным и другие свойства фигуры. Эти свойства называют следствиями из теоремы.
4. Все точки сходны между собою, и одна от другой могут отличаться только своим положением в пространстве. Наоборот, линии, кроме положения, занимаемого ими в пространстве, могут отличаться друг от друга формою. На чер. 1 нарисованы линии разных форм. Является вопрос: какую форму линии надо признать простейшею?

Для сравнительного разбора форм линий вообразим 2 точки A и B (точки называют, обыкновенно, большими буквами латинского алфавита) и какую-либо линию, произвольной формы, проходящую через эти точки, линию ACB (чер. 2). Следует заметить, что точки и линии, нарисованные на чертеже, не настоящие точки и линии, а только их грубые изображения, которыми мы пользуемся, чтобы облегчить свое воображение. Эту линию ACB можно вообразить вращающейся около точек A и B; от этого она не изменяет своей формы (на основании аксиомы п. 2).
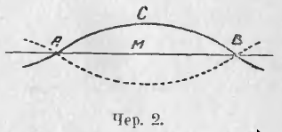
При вращении она, вообще говоря, занимает последовательно бесчисленное множество различных положений, всякой раз, однако, проходя через точки A и B. Одно из таких положений нарисовано на чер. 2 пунктиром. Следовательно, линий взятой формы удалось провести через 2 взятые точки бесчисленное множество. Если случится, что взятая линия вращается так, что остается на месте, не меняя своего положения (наше воображение позволяет нам утверждать, что такой случай возможен, какие бы 2 точки мы ни взяли), то окажется, что линий этой особенной формы возможно чрез 2 точки провести только одну. На черт. 2 такая форма изображена линиею AMB.
Естественно признать эту особенную форму линии простейшею, – называют такую линию прямой. Итак, мы признаем:
1) существуют прямые линии;
2) через всякие 2 точки можно провести прямую линию и только одну.
Кроме того, мы еще признаем, что прямая линия не имеет концов (бесконечная).
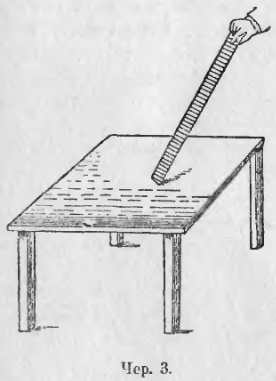
5. Более трудным является вопрос об изыскании самой простой поверхности. Сначала разберем чисто-практическую сторону дела. Если хотим узнать, как много неровностей и как они велики на поверхности стола, мы берем линейку, получше выверенную (ребро ее должно возможно приближаться к прямой линии), укладываем ее ребром в разных направлениях на поверхность стола и всякий раз смотрим на свет, много ли остается промежутков между столом и ребром линейки. Чем их меньше, тем ровнее испытуемая поверхность. Что значит прикладывать к поверхности стола ребро линейки? Если сделать так, чтобы ребро имело с поверхностью стола лишь одну общую точку (чер. 3), то ребро еще не будет приложено к столу. Надо вращением добиться того, чтобы какая-либо другая точка ребра пришла в совпадение с какой-либо точкою поверхности: тогда у ребра линейки и у поверхности стола окажется непременно 2 общих точки, и мы скажем, что ребро линейки приложено к столу. Возможно, что других общих точек у них вовсе не будет; возможно, что их будет бесчисленное множество.
Перейдем теперь к невещественным геометрическим формам. Пусть имеем какую-нибудь поверхность и также, как на практике, вообразим прямую линию, которая приложена к нашей поверхности, т. е. имеет с нею 2 общих точки. Здесь мы можем вообразить случай, на практике невозможный: между поверхностью и приложенною прямою вовсе нет промежутков, т. е. прямая совпадает с нашею поверхностью не только двумя, но и всеми ее точками. Теперь можно сказать, что по направлению кашей прямой поверхность вовсе не имеет неровностей. Можно вообразить поверхность, которая по всем направлениям не имеет неровностей, и такая поверхность признается нами простейшею, – она называется плоскою поверхностью или плоскостью. Итак, мы признаем:
1) существуют плоскости;
2) всякая прямая, имеющая с плоскостью две общих точки, совпадает с нею всеми своими точками.
6. Геометрические фигур разделяются на плоские и пространственные: плоскою фигурою называется фигура, всеми своими частями умещающаяся на одной плоскости, а пространственною называется фигура, не умещающаяся всеми частями на плоскости. Геометрия разделяется на 2 части: первая часть изучает плоские фигуры, – и она называется плоскою геометриею или планиметриею; вторая часть изучает пространственные фигуры, – и она называется пространственною геометриею или стереометриею.
Геометрию подразделяют еще 1) на чистую геометрию, где изучаются особенности расположения частей фигуры, и 2) на измерительную, где геометрические фигуры рассматриваются с точки зрения измерения. В чистой геометрии число появляется лишь как результат счета и не имеет первенствующего характера; в измерительной же геометрии число является основою (измерить значит выразить числом), и здесь геометрия сближается с арифметикою и алгеброю.
