180. Итак, если имеем 2 отрезка y и x, то можно составить уравнение, связывающее эти два отрезка, в виде (п. 168)

y/x = k или y = kx,

где k есть число рациональное или иррациональное.

Остановимся теперь на второй форме этого уравнения, т. е. y = kx.

Примем отрезок x за единицу, т. е. положим, что x = 1; тогда из предыдущего уравнения получим y = k, т. е., если отрезок x оценить числом 1, то отрезок y выразится числом k. Поэтому уравнение y = kx понимают так:

Мы измерили отрезок y, принимая за единицу отрезок x, причем в результате этого измерения получилось число k.

Вот примеры:

1) Длина комнаты = 8 ½ аршин,

т. е. мы измерили прямолинейный отрезок, называемый «длиною комнаты», принимая отрезок, называемый «аршином», за единицу, и получили в результате число 8 ½.

2) Рост этого человека 13/16 сажени,

т. е. мы измерили прямолинейный отрезок, выражающий рост этого человека, принимая за единицу сажень, и получили число 13/16.

3) Отрезок A = 0,377 отрезка B,

т. е. мы измерили отрезок A, принимая за единицу отрезок B, и получили число 0,377.

Тот отрезок, который принимается за единицу, называется линейною единицею: в 1-м примере линейною единицею служит аршин, во 2-м — сажень, в 3-м — отрезок B.

Следует заметить, что все предыдущие равенства могут быть даны и в другой форме:

1) длина комнаты / аршин = 8 ½;

2) рост этого человека/ сажень = 13/16;

3) отрезок A / отрезок B = 0,377,

т. е. «отношение длины комнаты к аршину = числу 8½, «отношение роста этого человека к сажени = числу 13/16», «отношение отрезка A к отрезку B = числу 0,377».

Таким образом, задача «измерить отрезок A, принимая отрезок B за единицу», совпадает с задачею «найти отношение отрезка A к отрезку B».

181. Всякие два отрезка y и x можно связать уравнением

y = kx,

где k какое-либо число целое, дробное или иррациональное. Другими словами: всякий отрезок может быть измерен, принимая какой-либо другой отрезок за линейную единицу, причем в результате измерения получится число целое, дробное или иррациональное.

Если число k окажется рациональным (целым или дробным), то предыдущее уравнение y = kx укажет нам, как можно из линейной единицы x получить измеряемый отрезок y (напр., если y = 3/7 x, то для получения y надо линейную единицу x разделить на 7 равных частей и взять 3 таких части).

Если число k окажется иррациональным, то уравнение y = kx таких указаний нам дать не может: ведь для нас иррациональное число и определено лишь, как отношение двух несоизмеримых отрезков (п. 168). В исключительных лишь случаях возможно, что это иррациональное число выразится каким-либо иным символом, напр., √2; тогда это обстоятельство может нам помочь получить отрезок y, выполняя некоторые построения над отрезком x.

Поэтому прибегают к приближенному измерению. В пп. 170 и 172 мы научились узнавать приближенные значения отношения двух отрезков: в п. 170 мы для этой цели пользовались умением делить отрезок на равные части, а в п. 172 обошлись без этого умения, причем, однако, в п. 170 мы могли найти приближенное значение с какой угодно, наперед заданною, точностью, а в п. 172 мы указали, что это было бы возможно лишь при знании теории непрерывных дробей.

Теперь нам придется обратиться к п. 170 с целью истолковать в другой форме полученные там результаты.

Возобновим чер. 185 и поставим задачу: измерить отрезок AB с точностью до 1/5, принимая отрезок CD за линейную единицу, причем будем считать, что AB и CD несоизмеримы. Мы получили в п. 170 два отрезка AK и AL, которые оба соизмеримы с линейною единицею CD, причем AK = 8/5 CD и AL = 9/5 CD. Так как AK < AB, но AL > AB, то отсюда вытекает

8/5 CD < AB < 9/5 CD.

Иногда то же самое записывают в виде:

AB = прибл. 8/5 CD (с недост.), или 9/5 CD (с изб.).

[Пояснение. Если вместо отрезка AB взять отрезок AK = 8/5 CD, то здесь чего-то «недостает» сравнительно с отрезком AB; поэтому в скобках пишем «с недостатком». Если вместо AB взять отрезок AL = 9/5 CD, то здесь имеется «избыток» сравнительно с отрезком AB; поэтому в скобках пишем «с избытком».]

Считая отрезок AB равным 8/5 CD, или 9/5 CD, мы в обоих случаях делаем ошибку, меньшую 1/5 CD. Поэтому мы говорим, что измерили отрезок AB с точностью до 1/5 линейной единицы CD.

Также точно могли бы измерить отрезок AB линейною единицею CD с точностью до 1/10 CD. Напр., могли бы получить

17/10 CD < AB < 18/10 CD

или AB = прибл. 17/10 CD (с недост.) или 18/10 CD (с избыт.).
В п. 170 имеются соответствующие записи об отношении AB/CD, а именно:

17/10 < AB/CD < 18/10 и AB/CD = прибл. 17/10 или = прибл. 18/10.

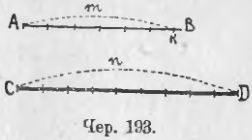
182. Мы можем предыдущую задачу решить в общем виде: измерить отрезок AB линейною единицею CD с точностью до 1/n CD. Разделим CD (чер. 193) на n равных частей и станем эти части укладывать на отрезке AB; пусть их уложилось m с остатком KB, причем KB < 1/n CD (всегда можно дойти до такой точки K — в этом состоит аксиома Архимеда. Отрезок AK = m/n CD, но он меньше отрезка AB, причем разность этих отрезков меньше 1/n CD; Поэтому мы можем принять, что

AB = прибл. m/n CD (с недост.).

Если отложить от точки K еще один раз n-ую часть единицы CD, то перейдем за точку B и получим отрезок = (m + 1)/n CD, который больше отрезка AB на отрезок, меньший 1/n CD. Поэтому опять имеем:

AB = прибл. (m + 1)/n CD (с избытк.).

Тоже самое можно записать в виде неравенств:

m/n CD < AB < (m+1)/n CD.

Заметим, что на практике применяют изложенный здесь способ приближенного измерения ко всяким отрезкам, не разбирая вопроса, соизмерим ли известных отрезок с линейною единицею или нет.

183. В п. 172, находя приближенные значения, отношения отрезков AB и CD (чер. 186) без умения делить отрезок на равные части, мы писали:

AB = (прибл.) 19/5 CD,

т. е. и здесь мы измеряли приближенно отрезок AB линейною единицею CD, хотя и не знали, с кокой именно точностью это выполняли.

Следует, однако, обратить внимание на п. 172, так как из него видно, что для измерения одного отрезка другим, или для нахождения отношение двух отрезков, умение делить отрезок на равные части вовсе не столь необходимо, как это могло показаться с первого взгляда.

184. Обращаясь к пп. 165 и 172, мы можем выяснить те свойства отрезков, которые необходимы для того, чтобы находить отношение двух отрезков, или, другими словами, чтобы выжать отрезки числами, принимая определенных отрезок за единицу.

Необходимо прежде всего умение откладывать один отрезок на другом, причем необходимо уметь различать, когда один отрезок равен другому или больше другого или, наконец, меньше другого (ведь все время в п. 165 и в п. 172 приходилось откладывать на одном отрезке части, равные другому отрезку, и о полученном остатке установить, что он меньше откладываемого отрезка).

Затем нам приходилось, например, в п. 165, писать равенства вроде

CD = 2AB + FD

или, более подробно:

CD = AB + AB + FD.

Писать подобные равенства мы можем лишь при условии знания, что значит сложить два отрезка. Итак, надо еще знать, что значит сложить два отрезка, причем должно быть установлено, что можно найти сумму всяких двух отрезков.

Все перечисленные знания относительно отрезков изложены в самом начале курса геометрии. Так как, последив пп. 165 и 172, мы увидим, что иных знаний относительно отрезков не требуется, то мы можем установить, что сведения, данные в пп. 8–10, об отрезках достаточны для умения находить отношение всякой пары отрезков.

Умение делить отрезок на равные части, которым мы пользовались в п. 182, несущественно, – это видно из п. 172.

Если имеем совокупность предметов, причем 1) для каждых двух предметов этой совокупности можно установить, равны ли они, или один из них больше другого и 2) можно установить понятие о сумме двух предметов этой совокупности (а, следовательно, и об их разности) *, то говорят, что эту совокупность предметов можно рассматривать, как систему величин. ( * Всякие два предмета этой совокупности должны иметь сумму.)

Совокупность прямолинейных отрезков можно рассматривать, как систему величин.

Каждый отдельных отрезок является значением этой системы величин.

Каждое значение системы величин может быть выражено числом, принимая другое ее определенное значение за единицу (каждый прямолинейных отрезок может быть выражен числом, принимая за единицу определенный отрезок).

Свойства прямолинейных отрезков, позволяющие их совокупность считать системою величин, выражают словами: всякий прямолинейный отрезок имеет длину.

На практике для измерения отрезков употребляются раз навсегда выбранные единицы, называемые линейными единицами. Вот наиболее употребительные линейные единицы: сажень, аршин, вершок, верста, фут, дюйм, метр, километр, сантиметр.

На практике не различают, соизмерим ли или нет данный отрезок с единицею, а всегда измеряют с какою-либо точностью. Например, если отрезок начерчен на бумаге, то к нему прикладывают линейку, на которой нанесены, например, дюймы, разделенные на 10 равных частей каждый, и смотрят, сколько целых дюймов и десятых долей дюйма укладывается на данном отрезке, пренебрегая остатком меньше половины десятой доли дюйма, или считая его за целую десятую долю дюйма, если он больше половины его.

185. Упражнения. 1. Даны два отрезка AB и CD. Найти AB/CD, полагая, что эти отрезки соизмеримы; найти затем CD/AB (или: измерить отрезок AB, принимая CD за линейную единицу и, наоборот, измерить CD, принимая AB за единицу).

2. Даны 2 отрезка. Найти приближенное значение их отношения, принимая, что третий остаток при отыскании их общей меры можно принять за их общую меру.

3. Даны 2 (несоизмеримых) отрезка. Найти их отношение с точностью до 1/8; затем найти с тою же точностью их обратное отношение (измерить с точностью до 1/8 первый отрезок, принимая второй за единицу, и, обратно, измерить с тою же точностью второй отрезок, принимая первый за единицу).