107. Мы знаем (п. 102), что геометрическим местом точек, равноотстоящих от двух данных параллельных прямых, служит средняя параллельная. Если таким образом AB и CD (чер. 114) суть две параллельные и MN для них средняя параллельная, то расстояния любой точки E этой средней параллельной от AB и CD равны между собою, т. е., построив EF ⊥ AB и EG ⊥ CD, получим, что EF = EG.
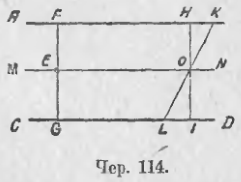
Ясно, что построенные перпендикуляры EF и EG составляют продолжение друг друга и образуют один отрезок FG, перпендикулярный к нашим параллельным AB и CD, причем этот отрезок делится среднею параллельною (в точке E) пополам. Итак, всякий отрезок, перпендикулярный к двум параллельным и заключенный между ними, делится среднею параллельною пополам.
Возникает теперь вопрос: не будет ли также делиться пополам среднею параллельною какой-нибудь отрезок KL, не перпендикулярный к AB и CD. Пусть KL пересекается с MN в точке O. Построим через точку O перпендикулярный к прямым AB и CD отрезок HI. Тогда OH = OI. Так как, кроме того, ∠HOK = ∠IOL, как вертикальные, то прямоугольные треугольники OHK и OIL равны, откуда следует, что OK = OL. Итак, оказывается, что и любой отрезок, заключенный между двумя параллельными, делится среднею параллельною пополам.
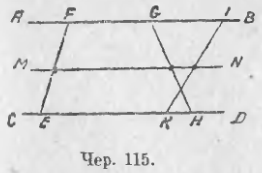
Пусть AB || CD (чер. 115). Построив между ними ряд каких-либо отрезков EF, GH, KI и т. д., мы, согласно предыдущему, найдем, что середины этих отрезков лежат на средней параллельной MN. В общем итоге мы приходим к следующему заключению:
Геометрическим местом середин всевозможных отрезков, заключенных между двумя параллельными, служит средняя параллельная.
Отсюда возникают возможности различных построений средней параллельной для двух данных параллельных прямых: 1) мы можем, построим любой отрезок EF, заключенный между двумя данными параллельными AB и CD, разделить его пополам и через его середину построить прямую MN || AB || CD — это прямая MN и должна служить среднею параллельною, и она должна делить пополам всевозможные отрезки (напр., GH, KI и т. д.), заключенные между AB и CD. 2) Мы можем построить два отрезка, напр., EH и KI, заключенные между AB и CD, разделить каждый из них пополам и через их середины построить прямую MN — она и должна служить среднею параллельною.
108. Применим свойства средней параллельной к знакомым нам фигурам и прежде всего треугольнику.
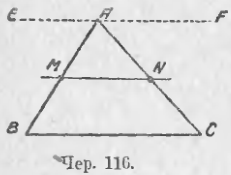
Пусть имеем ∆ABC (чер. 116). Здесь непосредственно мы не имеем двух параллельных, но мы всегда можем их получить, напр., построив через вершину A прямую EF || BC (эту прямую EF можно было бы и не рисовать на чертеже, так как она существенной роли не играет в дальнейшем и так как достаточно лишь знать, что она существует). Тогда мы имеем две параллельных BC и EF и два отрезка AB и AC, заключенных между ними. Разделив их пополам в точках M и N (AM = MB и AN = NC) и построив через M и N прямую MN, мы получим среднюю параллельную MN, т. е. MN || BC (и || EF, но это для нас не существенно). Из этого заключаем:
прямая, соединяющая середины двух сторон треугольника, параллельна его третьей стороне.
Отрезок, соединяющий середины двух сторон треугольника, называют среднею линиею треугольника. Итак, у нас отрезок MN есть средняя лини нашего треугольника.
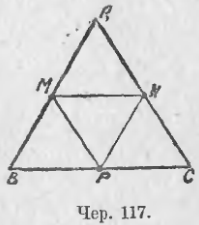
Пусть имеем ∆ABC (чер. 117). Разделим пополам каждую из его сторон: пусть M есть середина AB (сл. AM = MB), N — середина AC (AN = NC) и P — середина BC (BP = PC); соединим точки M, N и P отрезками MN, MP и PN, - каждый из этих отрезков является среднею линиею для нашего треугольника. Таким образом в треугольнике имеется три средних линии.
Согласно предыдущему, будем иметь: MN || BC, MP || AC и NP || AB. Поэтому AMPN, BMNP и PMNC суть параллелограммы. Так как в параллелограмме противоположные стороны равны, то имеем: MN = BP (из параллелограмма BMNP), но BP = BC/2 (ибо точка P есть середина BC); поэтому MN = BC/2. Также из параллелограмма AMPN получим: MP = AN = AC/2 и из параллелограмма AMPN — PN = AM = AB/2. Отсюда заключаем:
каждая средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей и равна ее половине.
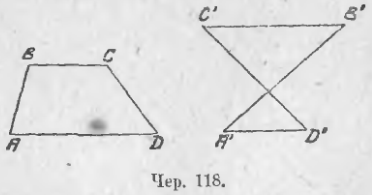
109. Перейдем теперь к четырехугольникам и остановимся сначала на таких четырехугольниках, у которых две стороны параллельны. Принято называть такие четырехугольники трапециями. На чер. 118 изображены два различных вида трапеций: 1) трапеция ABCD, где BC || AD, но AB не параллельна CD, - эта трапеция имеет площадь (см. п. 79) и 2) трапеция A'B'C'D', где A'D' || B'C', - эта трапеция не имеет площади (п. 79).
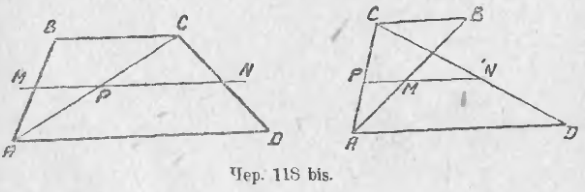
Рассмотрим сначала трапецию ABCD (чер. 118 bis), имеющую площадь. Здесь BD || AD. Поэтому мы имеем две параллельных BC и AD и между ними отрезки AB и CD. Разделив эти отрезки пополам в точках M и N (AM = MB и CN = ND) и соединив их прямою MN, получим среднюю параллельную MN для BC и AD, т. е. MN || BC || AD. Отрезок MN этой прямой называется средней линиею трапеции (следует добавить: «соединяющей середины непараллельных сторон», потому что в трапеции, как и во всяком четырехугольнике, можно рассматривать 6 средних линий, что имеет место в п. 110). Итак, мы получили, что MN || BC || AD. Далее, построив диагональ AC, получим еще третий отрезок AC, заключенный между параллельными BC и AD — его середина должна лежать (п. 107) на средней параллельной, т. е. точка P, где пересекаются MN и AC, есть середина отрезка AC. Поэтому MP есть средняя линия треугольника ABC и PN — средняя линия ∆ACD. На основании предыдущего, имеем: MP = BC/2 и PN = AD/2. Отсюда получаем: MN = MP + PN = BC/2 + AD/2 или MN = (BC + AD)/2. Итак,
средняя линия, соединяющая середины непараллельных сторон трапеции, имеющей площадь, параллельна ее параллельным сторонам и равна их полусумме.
Пусть теперь имеем трапецию ABCD (чер. 118 bis), неимеющую площади. Здесь также BC || AD и поэтому середины M и N сторон AB и CD лежат на средней параллельной, т. е. здесь также имеем: MN || BC || AD. Построив диагональ AC, получим отрезок AC, заключенный между параллельными BC и AD, и его середина, точка P, должна лежать на средней параллельной. Поэтому PM есть средняя линия треугольника ABC и, следовательно PM = BC/2; также PN есть средняя линия ∆ABC и, след., PN = AD/2. Так как MN = PN – PM, то получим MN = PN – PM = AD/2 – BC/2 или MN = (AD – BC) / 2. Итак,
средняя линия, соединяющая середины непараллельных сторон трапеции, неимеющей площади, параллельна ее параллельным сторонам и равна их полуразности.
110. Пусть имеем какой-либо четырехугольник ABCD (имеющий площадь) — (чер. 119). Найдем середины M, N, P и Q его сторон и соединим их попарно. Получим 6 средних линий четырехугольника.
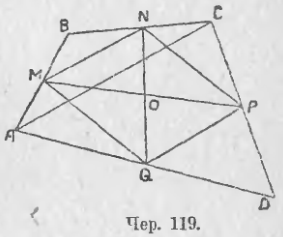
Вот свойства этих средних линий.
1) Средние линии, соединяющие середины последовательных сторон четырехугольника, образуют параллелограмм.
Для выяснения этого свойства построим диагональ AC. Тогда из ∆ABC имеем (п. 108) MN || AC и из ∆ACD на том же основании: PQ || AC, - следов., MN || PQ. Построив другую диагональ BD, найдем при ее помощи, что NP || MQ, следовательно, MNPQ есть параллелограмм.
2) Средние линии четырехугольника, соединяющие середины противоположных сторон, взаимно делятся пополам.
Это свойство теперь очевидно, так как MP и NQ являются диагоналями параллелограмма.
Через точку O пересечения прямых MP и NQ проходят также прямые, соединяющие середины диагоналей AC и BD (на чертеже диагональ BD не дана). Это следует из того, что AC И BD являются сторонами четырехугольника ACBD, не имеющего площади, к которому применимо все, изложенное в начале этого п.
111. Мы умели (пп. 57, 59) делить отрезок пополам и, следов., на 4, на 8 и вообще на 2n равных частей. Теперь мы можем разделить данный отрезок на 3, на 5 и вообще на сколько угодно равных частей.
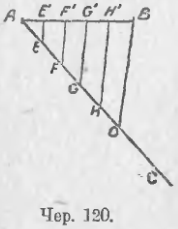
Пусть, напр., требуется отрезок AB (чер. 120) разделить на 5 равных частей. Построим через точку A произвольную прямую AC (образующую с AB угол, отличный от выпрямленного) и отложим на AC пять произвольных, но равных между собою, отрезков AE = EF = FG = GH = HO. Построим прямую OB и через точки E, F, G и Н построим прямые EE', FF', GG', HH', параллельные OB.
Рассмотрим ∆AFF', так как AE = EF, то E есть середина стороны AF и EE' (она || FF') есть средняя линия этого треугольника, следовательно, AE' = E'F'.
Рассмотрим затем трапецию EE'G'G. Так как EF = FG, FF' || EE', то FF' есть средняя линия трапеции EE'GG', - следовательно, E'F' = F'G'. Также найдем, что GG' есть средняя линия трапеции FF'H'H и, следов., F'G' = G'H' и т. д. Соединяя полученные равенства, найдем AE' = E'F' = F'G' = G'H' = H'B', т. е. отрезок AB разделился на 5 равных частей.
Из решения этой задачи можно вывести заключение:
Если на одной стороне угла отложить равные отрезки и чрез их концы построить ряд параллельных прямых, то и на другой стороне угла получим равные между собой отрезки.
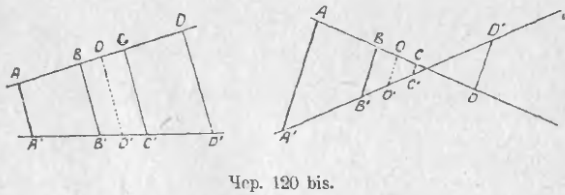
Добавление. Мы откладывали равные отрезки на одной прямой подряд, начиная от точки пересечения двух прямых (AB и AC чертежа 120), но возможно к такому же результату прийти и при ином способе отложения равных отрезков. На чертеже 120 bis дано два варианта такого построения: на прямой AD (см. чер. 120 bis слева или справа) отложим два равных отрезка AB и CD и через их концы построим параллельные AA' || BB' || CC' || DD'. Затем возьмем точку O, середину отрезка BC, и построим OO' || BB' || CC' || AA' || DD'. Тогда OO' есть средняя линия трапеции BCC'B'; поэтому B'O' = O'C (п. 109). Так как AB = CD и BO = OC, то AO также = OD; поэтому OO' есть также средняя линия трапеции ADD'A' (на чертеже справа эта трапеция ADD'A' — не имеющая площади, см. п. 109) — и также A'O' = O'D'. Отсюда имеем A'O' – B'O' = O'D' – O'C' (ибо и уменьшаемые и вычитаемые обеих разностей равны), или A'B' = C'D'. Возможны и иные комбинации (напр., отр. CD правой фигуры отодвинуть так, чтобы точка C оказалась правее точки пересечения прямых AD и A'D'). Общее заключение таково: если построены две прямые, на одной из них отложены как-либо два равных отрезка и через концы их построены параллельные, то эти последние выделят и на другой прямой два равных между собою отрезка.
112. Упражнения.
- Через вершины данного треугольника построены прямые, параллельные его сторонам. Показать, что новый треугольник имеет стороны вдвое больше, чем стороны данного, и что вершины данного являются серединами сторон нового (сравн. упр. 7 из п. 54).
- Построить треугольник, если даны середины трех его сторон.
- Построить параллелограмм, если даны середины трех его сторон.
- Известно (п. 110), что середины четырех сторон четырехугольника являются вершинами параллелограмма. Когда этот параллелограмм обращается в ромб, когда в прямоугольник, когда в квадрат?
- Прямая, соединяющая вершину треугольника со срединою противоположной стороны (медиана) и прямая, соединяющая середины двух других сторон треугольника, взаимно делятся пополам.
- Продолжим одну сторону треугольника на отрезок, равный этой стороне, и соединим конец отрезка со срединою другой стороны. Последняя соединяющая прямая отсекает от третьей стороны треугольника отрезок, равный 1/3 этой стороны. (Построить еще прямую, параллельную последней соединяющей прямой чрез вершину треугольника, противолежащую той его стороне, которая была продолжена).
- Если на стороне AB параллелограмма ABCD отложить отрезок AM = (1/n)AB (напр., (1/7)AB) и соединить D с M, то DM пересечет диагональ AC в точке N так, что AN = (1/(n+1))AC (во взятом примере (1/8)AC).
Для выяснения этого надо на продолжении стороны AB отложить BM' = AM и соединить C с M'; тогда C'M' || DM, – приметь п. 111.
