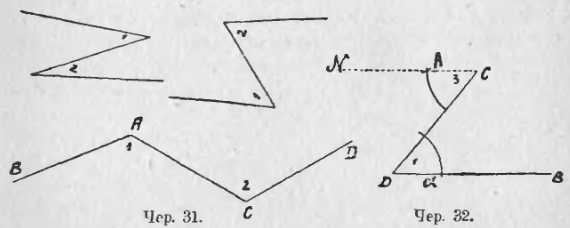
29. Нарисуем от руки несколько зигзагов, вроде данных на чер. 31. В каждом из этих зигзагов мы видим по 2 угла (они занумерованы нумерами 1 и 2 в каждом зигзаге чертежа 31). Каждый зигзаг состоит из двух лучей и отрезка, соединяющего точки, из которых исходят лучи. Напр., в последнем зигзаге имеем: 1) луч AB, исходящий из точки A, 2) луч CD, исходящий из точки C и 3) отрезок AC. Углы 1-ый и 2-ой принято называть внутренними накрест-лежащими углами по отношению к лучам, составляющим этот зигзаг. Упражнения должны приучить глаз к расположению таких углов.
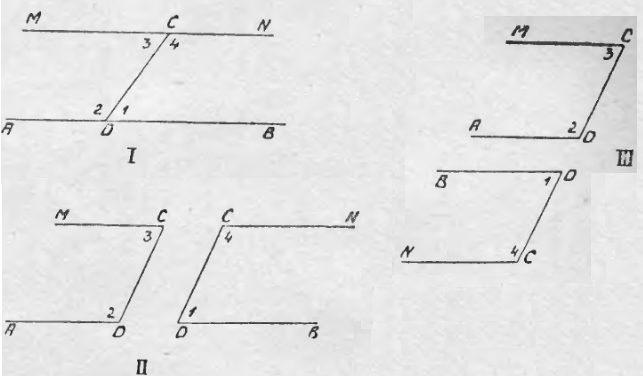
Построим теперь зигзаг так, чтобы его углы были бы равны между собою. Для этого начнем построение с произвольного угла BDC (чер. 33, I) или с ∠1; затем, закрепив точку C, построим при ней, согласно п. 28, ∠3 (или ∠MCD) = ∠1.
Для большей ясности воспроизводим это построение здесь на чер. 32.
1) строим ◡α, принимая точку D за центр, произвольным радиусом;
2) тем же радиусом строим ◡β, принимая точку C за центр;
3) берем циркулем хорду дуги α, соответствующую углу 1-му – концами ее служат точки пересечения дуги α с лучом DB и отрезком DC;
4) эту хорду откладываем на ◡β от точки пересечения этой дуги с отрезком DC, наблюдая, чтобы угол при точке C, соответствующий этой хорде, оказался внутренним накрест-лежащим с ∠1;
5) соединив конец этой хорды с точкою C, получим ∠3 = ∠1, причем эти углы – внутренние накрест-лежащие.
Тогда получим требуемый зигзаг MCDB. Если лучи MC и DB продолжить (CN есть продолжение луча CM и DA – продолжение DB), то получим еще второй зигзаг NCDA, внутренние накрест-лежащие углы которого обозначены нумерами 2 и 4. В общем, полученная фигура состоит из трех прямых MN, AB и CD, причем в последней заведомо известно, что она пересекает MN в точке C и AB в точке D, почему мы и будем прямую CD называть секущей.
Разучим полученную фигуру.
1. Мы видим, что ∠1 и ∠2 смежные, т. е. видим, что
∠1 + ∠2 = выпр. углу.
Также видим, что ∠3 и ∠4 смежные, т. е.
∠3 + ∠4 = выпр. углу.
Но мы строили ∠3 = ∠1. Поэтому заключаем, что обязательно ∠4 должен равняться ∠2. Итак, оказалось, что и вторая пара внутренних накрест-лежащих углов (∠2 и ∠4) состоит из равных углов. Это обстоятельство заслуживает внимания, и мы его можем запечатлеть словами: если две прямые пересечены секущею и если два внутренних накрест-лежащих угла равны между собою, то и другие два внутр. накр.-леж. угла тоже равны. (Всякое свойство фигуры, выраженное словами и полученное после некоторых рассуждений, называется теоремою. Здесь мы имеем теорему о внутренних накрест-лежащих углах.)
2. Всю фигуру, данную на чер. 33, I, мы расчленим на 2 фигуры: фигуру MCDA и фигуру NCDB – мы будем их называть «левою» и «правою» фигурами. Для ясности представим эти фигуры отдельно (чер. 33, II). У них имеется по равному отрезку: отр. CD левой фигуры равен отрезку CD правой, так как ранее эти отрезки совпали. Наложим, пользуясь этим равенством, правую фигуру на левую (понадобится правую фигуру повернуть, как на чер. 33, III, а затем накладывать на левую) так, чтобы точка D правой фигуры совместилась с точкою C левой и чтобы отрезок DC правой пошел по отрезку CD левой; в силу их равенства и другие их концы совместятся. Так как затем по построению ∠3 = ∠1, то луч DB правой фигуры должен пойти по лучу CM левой, в силу же выясненного равенства ∠2 и ∠4, луч CN правой фигуры должен пойти по лучу DA левой. Отсюда заключаем, что наши фигуры равны (это слово «равны» в геометрии и означает, что одна фигура совмещается при наложении с другой).
3. Обращаясь опять к чер. 33, I, мы можем спросить: пересекаются ли прямые MN и AB? Если предположить, что они пересекаются и точка пересечения расположена справа от секущей CD, то, в силу равенства правой и левой фигуры, мы должны прийти к заключению, что и слева от секущей CD должно быть то же, что и справа, т. е. и слева должна быть точка, через которую проходят обе прямые и MN и AB. Тогда оказалось бы, что через 2 точки проходят две прямые MN и AB, что невозможно. Следовательно, предположение, что AB и MN пересекаются справа от секущей, не годится. Ясно, что также нельзя допустить, что они пересекаются слева от секущей. Поэтому приходим к заключению, что нам удалось построить две прямые AB и MN, которые друг с другом вовсе не пересекаются.
Две прямые, расположенные на одной плоскости и не пересекающиеся, называются параллельными прямыми.
Для обозначения параллельности двух прямых употребляют знак ||; таким образом мы имеем MN || AB (MN параллельна AB). Из предыдущего построения вытекает:
можно построить параллельные прямые
или:
параллельные прямые существуют.
Мы можем фигуру, данную на чер. 33 (I), строить в ином порядке: 1) построим произвольную прямую AB (будем называть данною); 2) вне ее построим произвольную точку C (ее также будем называть данною); 3) через точку C строим секущую CD, образующую с данною прямою AB ∠1 и ∠2; 4) при точке C строим ∠3 = ∠1 так, чтобы эти углы оказались внутренними накрест-лежащими – получим луч CM; 5) продолжаем луч CM по направлению CN – тогда получим прямую MN, параллельную AB.
Отсюда вытекает заключение:
Через точку, данную вне данной прямой, всегда можно построить прямую, параллельную данной.
Так как для построения параллельных прямых необходимо было построить равные внутр. накрест-лежащие углы (∠3 = ∠1), то заключаем еще, что
если две прямые пересечены секущею и если полученные внутренние накрест-лежащие углы равны, то эти прямые параллельны.
30. В предыдущем п. мы научились строить через данную точку прямую, параллельную данной. Возникает теперь вопрос: сколько можно построить через данную точку прямых, параллельных данной? Ответ на этот вопрос возможен лишь на основе нашего представления о расположении параллельных прямых: если мы представим, что прямая MN (чер. 33, I), которая || AB, повернется около точки C в том или ином направлении, то нам ясно, что параллельность нарушится и что тогда MN где-либо с одной стороны от секущей CD пересечется с AB; может быть эта точка пересечения окажется так далеко, что на чертеже мы не будем в состоянии ее изобразить, но от этого наша уверенность в том, что прямая AB и повернутая прямая MN пересекаются, не уменьшится. Рассуждениями, основанными на предыдущем, подкрепить эту уверенность оказывается невозможным. Поэтому принимают, только на основании нашего представления, что
через точку, данную вне прямой, можно построить только одну прямую, параллельную данной.
Впервые это положение введено в науку знаменитым греческим геометром Евклидом, который дал полный систематический курс геометрии (за 300 лет до Р. Х.). Это свойство озаглавлено им именем «XI аксиома», которая выражена несколько иначе, чем здесь, но ее основная мысль та же самая. Иногда это же свойство называют именем «V постулат Евклида». Разница между этими двумя названиями следующая: аксиомами называют такие свойства, которые очевидны сразу, и мысль о том, что их нельзя путем рассуждений вывести из других свойств, уже установленных, появляется при тщательном рассмотрении системы геометрии; постулатами называют допущения, которые необходимо принять, чтобы идти дальше, но справедливость которых не столь очевидна. Впрочем, разница между этими двумя понятиями столь незначительна, что их часто смешивают.
В тех словах, которыми мы здесь выразили постулат Евклида о параллельных, заключаются 2 мысли: 1) через точку можно построить прямую, параллельную данной, – эта мысль отнюдь не относится к содержанию постулата: в п. 29 мы выяснили возможность такого построения; 2) только одну параллельную, – эта мысль, выражаемая словами «только одну», и составляет содержание постулата.
31. Из постулата о параллельных сейчас же вытекает несколько новых свойств, которые поэтому можно назвать следствиями из постулата о параллельных.
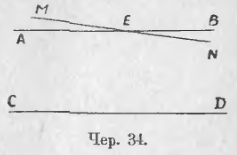
I. Пусть построено: 1) AB || CD (чер. 34); 2) прямая MN, пересекающая AB в точке E. Возникает вопрос: пересекаются ли MN и CD?
Ответ ясен: нельзя допустить, что MN не пересекает CD, – тогда бы через точку E оказались бы построенными две прямых AB и MN, параллельных CD, что противоречит постулату о параллельных.
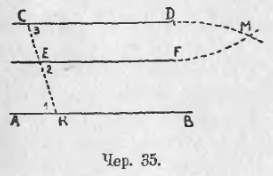
II. Пусть построено: 1) EF || AB и 2) CD || AB (чер. 35) (для этого построения удобно воспользоваться только одною секущею CEK и построить ∠2 = ∠1 и ∠3 = ∠1). Возникает вопрос: пересекаются ли или нет прямые CD и EF?
Допустим, что CD и EF пересекаются в точке M; тогда оказалось бы, что через M построены две прямые MDC и MFE, параллельные порознь прямой AB, что противоречит постулату о параллельных. Отсюда приходим к заключению, что CD || EF. Возможен, конечно, случай, что данные точки C и E расположены так, что построенные через них прямые, параллельные AB, сливаются в одну. Итак, имеем:
Если через каждую из двух данных точек построить прямую, параллельную данной, то построенные прямые или параллельны между собою или сливаются в одну прямую.
На основании этого случай совпадения двух прямых часто рассматривают, как частный случай параллельности.
III. Пусть построено: 1) AB || CD при помощи секущей MN (чер. 36) и 2) секущая EF, причем образовались при точках пересечения E и F внутр. накр.-лежащие углы, напр., ∠1 и ∠4. Возникает вопрос: равны ли между собою эти углы?
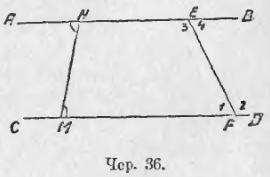
Рассмотрим точку E. Мы знаем (п. 29), что через эту точку можно построить прямую, параллельную CD, для чего можно воспользоваться секущею EF и построить при точке E угол, равный ∠1 так, чтобы он был внутренним накрест-лежащим с ∠1; с другой стороны, на основании постулата (п. 30), мы знаем, что можно построить лишь одну параллельную, а она уже построена – AB || CD, причем луч EB образует с секущею EF ∠4, внутренний накрест-лежащий с ∠1. Поэтому мы заключаем, что этот ∠4 необходимо должен быть равным ∠1. Итак,
Если две параллельных пересечены секущею, то внутренние накрест-лежащие углы равны.
32. Вообразим, что секущая EF (чер. 36) продолжена в обе стороны; тогда получим фигуру, данную на чер. 37, причем при точках E и F мы имеем 8 углов (они занумерованы нумерами 1-8 уже в ином порядке, сравнительно с чер. 35). Мы теперь видим, что 1) ∠1 = ∠4 (как вертикальные) = ∠5 (как внутр. накрест-лежащие) = ∠8 (как вертикальные); 2) ∠2 = ∠3 (как вертикальные) = ∠6 (как внутр. накрест-лежащие) = ∠7 (как вертикальные).
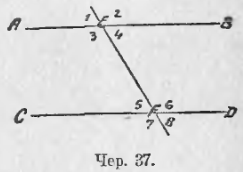
Таким образом, все 8 углов разбиваются на 2 группы: 1) ∠1, ∠4, ∠5 и ∠8 и 2) ∠2, ∠3, ∠6 и ∠7. Углы одной группы все между собою равны, но какой-либо угол из одной группы вообще не равен углу другой группы. Но зато мы видим, что, напр.,
∠5 + ∠6 = выпр. углу.
Так как каждый из остальных углов первой группы равен ∠5-му и каждый из остальных углов второй группы равен ∠6-му, то заключаем, что сумма любого угла первой группы с любым углом второй группы равна выпрямленному углу. Итак:
Если две параллельных пересечены секущею, то полученные 8 углов разделяются на две группы по 4 угла в каждой: углы каждой группы равны между собою и сумма двух углов, из которых один угол принадлежит одной группе, а другой угол – другой группе, равна выпрямленному углу.
Обратим внимание на отдельные пары углов, причем в пары будем соединять углы, один из которых при вершине E, а другой при вершине F.
Мы уже знаем, что ∠4 = ∠5 и ∠3 = ∠6, т. е., что внутренние накрест-лежащие углы равны.
Из первой группы мы имеем еще ∠1 = ∠8. Эти углы (∠1 и ∠8) расположены по разные стороны секущей и их внутренние области расположены вне полосы, выделяемой прямыми AB и CD. Поэтому их называют внешними накрест-лежащими углами. Во 2-й группе имеется также пара таких углов: ∠2 и ∠7, причем ∠2 = ∠7. Итак, при параллельных прямых внешние накрест-лежащие углы равны.
Из первой группы имеем ∠1 = ∠5. Эти 2 угла расположены по одну сторону секущей и один из них внешний (∠1), а другой внутренний (∠5). Такие два угла называются соответственными. Мы имеем еще пары соответственных углов: ∠4 = ∠8 (оба в I группе), ∠2 = ∠6 (оба во II группе), ∠3 = ∠7 (оба во II группе). Итак, соответственные углы при параллельных равны между собою.
∠3 принадлежит ко II группе, а ∠5 – к I; поэтому ∠3 + ∠5 = выпрям. углу. Оба этих угла расположены по одну сторону от секущей и оба они внутренние. Поэтому их называют внутренними односторонними углами. Имеется еще пара таких же углов: ∠4 и ∠6; для них (так как они принадлежат к разным группам) также имеем ∠4 + ∠6 = выпрям. углу. Итак, внутренние односторонние углы при параллельных составляют в сумме выпрямленный угол.
Пары: 1) ∠1 и ∠7 и 2) ∠2 и ∠8 называются внешними односторонними углами и для них имеем (ибо углы каждой пары принадлежат к разным группам):
∠1 + ∠7 = выпр. углу; ∠2 + ∠8 = выпр. углу,
т. е. внешние односторонние углы при параллельных составляют в сумме выпрям. угол.
Наконец, пары: 1) ∠1 и ∠6, 2) ∠2 и ∠5, 3) ∠3 и ∠8 и 4) ∠4 и ∠7 особого названия не имеют, но каждая пара состоит из двух углов, один из которых внешний, а другой внутренний, причем они расположены по разные стороны секущей. Так как углы каждой пары принадлежат разным группам, то имеем:
∠1 + ∠6 = выпр. углу; ∠2 + ∠5 = выпр. углу; ∠3 + ∠8 = выпр. углу; ∠4 + ∠7 = выпр. углу,
т. е. при параллельных пара разносторонних углов, из которых один внутренний, а другой внешний, в сумме составляют выпрямленный угол.
33. Не трудно теперь видеть, что параллельные прямые можно строить при помощи других пар углов, не внутренних накрест-лежащих, как в п. 29. В самом деле, построим при точке E (чер. 37) ∠1 = ∠5 так, чтобы эти углы были соответственными. Тогда найдем, что ∠1 = ∠4 и, след., ∠4 = ∠5, т. е., что AB || CD. Также можно пользоваться и внешними накр.-леж. углами (если ∠1 = ∠8, то и ∠4 = ∠5, т. е., что AB || CD. Также можно пользоваться и внешними накр.-леж. углами (∠1 = ∠8, то и ∠4 = ∠5 и прямые параллельны). Можно также строить внутренние односторонние углы так, чтобы их сумма равнялась выпрямленному углу (если ∠3 + ∠5 = выпрям., то ∠4 = ∠5, так как ∠3 + ∠4 = выпрям., – след., AB || CD); можно также пользоваться и внешними односторонними углами. Итак:
Если две прямые пересечены секущею и если внутренние накрест-лежащие углы равны, или если внешние накрест-лежащие углы равны, или если соответственные углы равны, или если сумма внутренних односторонних углов равна выпрямленному, или если сумма внешних односторонних углов равна выпрямленному, или если сумма двух разносторонних углов, из которых один внутренний, а другой внешний, равна выпрямленному, то прямые параллельны.
Для построения двух параллельных прямых обычно (и это удобнее всего) пользуются или внутренними накрест-лежащими углами или соответственными.
Добавление. Постулат о параллельных прямых (п. 30) может быть выражен в такой форме:
Если сумма одной пары внутренних односторонних углов меньше выпрямленного угла, а следовательно сумма другой пары больше выпрямленного, то эти прямые пересекаются с той стороны от секущей, где сумма меньше выпрямленного.
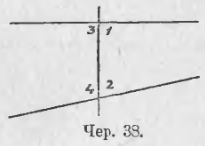
Если, например, ∠1 + ∠2 < выпр. угла (чер. 38), то, следовательно, ∠3 + ∠4 > выпрямленного угла, так как ∠1 + ∠3 = выпрям. углу и ∠2 + ∠4 = выпрям. углу. Наши прямые пересекаются с той стороны секущей, где расположены ∠1 и ∠2. В этой именно форме и был дан постулат о параллельных Евклидом.
34. Упражнения. 1. Построить через данную точку (см. различные положения, данные на чер. 39) прямую, параллельную данной.
На 1-м чертеже построение выполнено: из A строим секущую AB; из точки B, как центра, строим дугу и таким же радиусом (удобнее этот радиус брать небольшим) описываем дугу, принимая A за центр. Затем при A строим угол, равный ∠B, чтобы получились 2 внутр. накр.-леж. угла, и т. д.
2. Построить пару параллельных прямых в каком угодно положении.
3. Даны 2 пересекающихся прямых; построить через данную точку две новых прямых, параллельных соответственно двум данным.
4. Построить две пары параллельных прямых в каком угодно положении, но чтобы все 4 прямые не были между собою параллельны.
35. Построены две пары параллельных прямых: 1) c || b и 2) d || a (чер. 40) (каждая прямая названа одною малою буквою). При точке пересечения прямых a и b получились углы, рассмотрим один из них, именно ∠1, и сравним его с углами 2, 3, 4 и 5-м, полученными при пересечении прямых c и d.
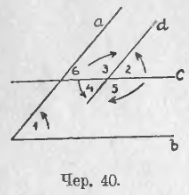
Продолжим прямую c до пересечения с прямой a, – при точке пересечения получим еще углы, один из которых обозначен нумером 6. Тогда имеем: 1) ∠2 = ∠6, как соответственные при параллельных a и d и секущей c; 2) ∠6 = ∠1, как соответственные при параллельных c и b и секущей a. Следовательно, ∠2 = ∠1. Так как ∠4 = ∠2, то и ∠4 = ∠1. Так как ∠3 + ∠2 = выпр. углу. Заметив, что стороны ∠1 параллельны сторонам любого из углов 2, 3, 4 и 5, найдем:
Если стороны двух углов попарно параллельны, то эти углы или равны между собою или в сумме составляют выпрямленный угол.
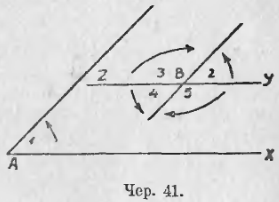
Возникает вопрос: нельзя ли установить признак, пользуясь которым можно было бы разделить эти 2 случая. Для этой цели станем смотреть на угол, как на результат вращения луча и начальным положением будем считать такое расположение лучей, когда они в ∠1 и в одном из углов 2, 3, 4 или 5 располагаются параллельно, например, по прямым b и c. Тогда стрелки, данные на чертеже, укажут направление, в котором надо вращать луч, чтобы получить желаемый угол. Удобно сравнивать это направление с движением часовой стрелки. Видим, что для получения ∠1 надо луч AX (чер. 41) вращать против часовой стрелки, для ∠2 надо луч BY (BY || AX) вращать против часовой стрелки, для получения ∠3 надо луч BZ вращать по часовой стрелке и для ∠5 – луч BY по часовой стрелке. Отсюда можно вывести, что углы с параллельными сторонами равны, если направления их вращения одинаковы, и что такие углы дополняют друг друга до выпрямленного угла, если направления их вращения противоположны.