50. Построим две пары параллельных прямых: AB ∥ CD и AD ∥ BC (чер. 57). Совокупность этих четырех прямых с их четырьмя точками пересечения составляют фигуру, называемую параллелограммом. На чер. 57 имеем параллелограмм ABCD. Прямые, его составляющие, называются сторонами параллелограмма; иногда под этим названием понимают не всю бесконечную прямую AB, а только ее отрезок между точками A и B. Точки пересечения сторон называются вершинами параллелограмма. Параллелограмм выделяет из плоскости определенную ее часть, называемую его площадью. Параллелограмм имеет 4 внутренних угла; поэтому иногда дают определение параллелограмма в следующей форме:
Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны.
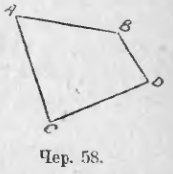
Параллелограмм является, следовательно, частным видом общего понятия «четырехугольник»; мы легко можем построить вообще какой-нибудь четырехугольник, выделяющий из плоскости определенную ее часть: для этого надо построить какой-нибудь отрезок AB (чер. 58), из точки A построить какой-либо новый отрезок AC, составляющий с AB угол, отличный от выпрямленного, из точки C также построить новый отрезок CD, чтобы точка D лежала по ту же сторону прямой AC (бесконечной), как и точка B, и, наконец, построить отрезок BD, концами которого служат уже построенные точки B и D. То же можно выполнить иначе: взять 4 произвольных точки A, B, D и C и соединить их попарно прямыми, каждую с двумя соседними, наблюдая лишь, чтобы эти прямые выделяли из плоскости определенную часть.
О четырехугольниках и вообще о многоугольниках смотри гл. VII.
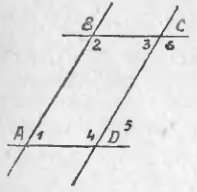
51. Изучение углов параллелограмма. Пронумеруем внутренние углы цифрами 1, 2, 3 и 4 и возьмем еще два из внешних углов: ∠5 и ∠6 (чер. 57). Тогда:
1) ∠1 + ∠4 = выпрямл. углу; 2) ∠1 и ∠2 = выпрямленному углу и т. д.
В самом деле, углы 1 и 4 суть внутренние односторонние при параллельных AB и DC и секущей AD, а мы знаем (п. 33), что сумма таких углов равна выпрямленному; то же применимо и к углам 1 и 2, которые являются внутренними односторонними при параллельных AD и BC и секущей AB. Можно то же применить и к парам углов 2 и 3 или к 3 и 4.
2) ∠1 = ∠3 и ∠2 = ∠4.
Так как ∠1 = ∠5, как соответственные при параллельных AB и DC и секущей AD, но ∠5 = ∠3, как внутренние накрест-лежащие углы при параллельных AD и BC и секущей CD, то ∠1 = ∠3; также найдем: ∠4 = ∠6 и ∠6 = ∠2, следов., ∠4 = ∠2.
Эти результаты можно выразить словами:
В параллелограмме: 1) два соседних угла в сумме составляют выпрямленный угол и 2) два противоположных угла равны между собою.
52. Изучение сторон параллелограмма. Здесь мы будем рассматривать стороны, как отрезки, а потому изобразим параллелограмм так, как на чер. 59.
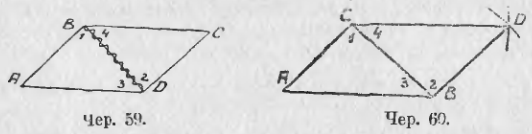
Точки A, B, C и D (чер. 57), кроме сторон, определяют еще прямые AC и BD (на чер. 57 они не начерчены), называемые диагоналями параллелограмма. Построив только одну из них BD (чер. 59), получим два треугольника: ∆ABD и ∆DBC, у которых одна сторона BD общая. Кроме того, пронумеровав углы, составляемые диагональю BD со сторонами параллелограмма, как на чертеже, найдем ∠1 = ∠2, как внутренние накрест-лежащие при параллельных AB и DC и секущей BD, затем ∠3 = ∠4, как внутренние накрест-лежащие при параллельных AD и BC и секущей BD. Следовательно два угла (∠1 и ∠3) и сторона между ними BD одного треугольника (∆ABD) соответственно равны двум углам (∠2 и ∠4) и стороне между ними (DB) другого треугольника (∆CDB), поэтому (п. 47) и ∆ABD = ∆CDB. Отсюда заключаем, что и их остальные части равны, причем равные стороны должны лежать против равных углов: AD (против ∠1 в ∆ABD) должна, следовательно, равняться BC (против ∠2 в ∆CDB) и также AB (против ∠3) равняется DC (против ∠4). Этот результат можно выразить словами:
Параллельные стороны параллелограмма равны между собою.
53. В упражнениях 3 и 4 п. 34 мы уже строили параллелограмм. Но построение параллельных прямых несколько длинно. Теперь является возможным ускорить построение параллелограмма. Возьмем произвольный угол A (чер. 60) и на сторонах его отложим два произвольных отрезка AB и AC; затем, принимая B за центр, построим окружность радиусом, равным отрезку AC, и, принимая C за центр, построим другую окружность, радиусом, равным отрезку AB. Наконец, одну из точек пересечения этих окружностей, ту именно, которая лежит внутри взятого угла A, соединим прямыми DC и DB с точками C и B. На нашем чертеже даны только дуги этих кругов, которых достаточно для определения положения точки D; на практике так всегда и поступают. Тогда получим четырехугольник DBAC, выделяющий из плоскости ее определенную часть; согласно построению, 1) BD = AC и 2) AB = CD. Возникает вопрос: построен ли у нас параллелограмм, или нет?
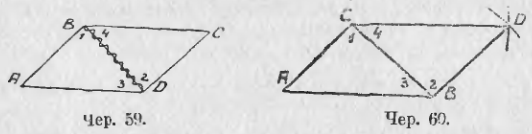
Для решения этого вопроса построим диагональ CB; тогда получим 2 треугольника: ACB и DBC, у которых сторона CB общая и, согласно построению, AC = BD и AB = CD, т. е. 3 стороны одного треугольника равны соответственно трем сторонам другого, а такие треугольники, мы знаем (п. 46), равны, т. е. ∆ACB = ∆CBD. Отсюда заключаем о равенстве углов 1 и 2 (против равных сторон); следов., AC ∥ BD, так как ∠3 = ∠4, и, следов., AB ∥ CD, так как ∠3 и ∠4 суть внутренние накрест-лежащие углы при прямых AB и CD и секущей CB. Отсюда следует, что ACDB есть параллелограмм, т. е.:
Если построен 4-угольник, выделяющий из плоскости определенную часть, у которого противоположные стороны равны, то этот 4-угольник есть параллелограмм.
54. Упражнения. Надо освоиться с выше данным построением параллелограмма и выполнять это построение быстро и свободно.
- На данном угле построить параллелограмм. Много ли таких параллелограммов возможно построить?
- Построить параллелограмм на данной стороне. Много ли возможно построить таких параллелограммов?
- Построить параллелограмм по данной стороне и по углу. Много ли таких параллелограммов можно построить?
- Построить параллелограмм по двум сторонам. Много ли таких параллелограммов можно построить?
- Построить параллелограмм по двум сторонам и углу между ними.
- Построить параллелограмм на данной диагонали. Много ли возможно построить таких параллелограммов?
- Построить параллелограмм, если даны три его вершины. Сколько можно построить таких параллелограммов?
После решения этой задачи получим фигуру, изучение которой позволит установить некоторые свойства треугольника:
а) прямая, соединяющая середины двух сторон треугольника, параллельна третьей его стороне и равна ее половине;
б) если дан какой-либо треугольник, то можно построить другой треугольник, чтобы каждая сторона нового была в 2 раза больше (или, наоборот, в 2 раза меньше) соответствующей стороны старого треугольника, причем площадь нового треугольника окажется в 4 раза больше (или, наоборот, – меньше) площади старого.
(На стран. 99 дана фигура, которую можно получить здесь, решая предложенную задачу; в п. 107, на той же странице, дано изучение этой фигуры, однако, с несколько иной точки зрения). - 8. Построить параллелограмм по двум сторонам и диагонали.
Полезно, прежде чем приступить к построениям, требуемым в вышеизложенных задачах, дать себе отчет, какие из 4 вершин параллелограмма даны, и наметить мысленно заранее приблизительное положение остальных вершин.
55. Можно еще построить параллелограмм следующим образом: построим две параллельных прямых AB ∥ DC (чер. 61) и на каждой из них отложим по равному отрезку AB = DC. Затем соединим точки A и D и точки B и С (но нельзя соединять A с C и B с D, – тогда получится 4-угольник, не выделяющий из плоскости определенную ее часть); тогда получим 4-угольник ABCD, у которого AB ⊫ DC (равна и параллельна), выделяющий из плоскости определенную ее часть.
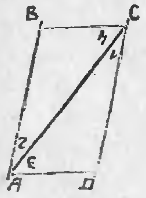
Не трудно выяснить, что построенный 4-угольник есть параллелограмм. Для этого построим диагональ AC и пронумеруем полученные при концах диагонали углы. Легко видеть, что ∆ABC = ∆CDA; в самом деле, у них сторона AC общая, затем по построению AB = CD и, кроме того, ∠1 = ∠2, так как AB ∥ CD, т. е. 2 стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого, а мы знаем (п. 47), что в этом случае треугольники равны. Отсюда заключаем, что ∠3 = ∠4, а так как эти углы суть внутренние накрест-лежащие при прямых CB и AD и секущей CA, то CB ∥ AD; кроме того, из равенства же треугольников имеем CB = AD. Теперь выяснено, что ABCD есть параллелограмм. Этот результат можно выразить словами:
Если в четырехугольнике, выделяющем из плоскости определенную ее часть, две стороны равны и параллельны, то и другие две равны и параллельны, и этот четырехугольник есть параллелограмм.
56. Изучение диагоналей параллелограмма. Уже было замечено, что в параллелограмме возможно построить две диагонали. Пусть построен параллелограмм ABCD (чер. 62) и его диагонали AC и BD. Мы уже знаем, что противоположные стороны параллелограмма равны, т. е. AB = CD и AD = BC. Воспользуемся этим и найдем равные треугольники.
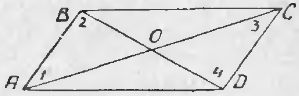
Нетрудно увидать, что ∆AOB = ∆COD. В самом деле, мы знаем, что AB = CD; затем, пронумеровав углы, найдем, что ∠1 = ∠3, как внутренние накрест-лежащие при параллельных AB и CD и секущей AC, а также ∠2 = ∠4, как внутренние накрест-лежащие при параллельных AB и CD и секущей BD, т. е. два угла и сторона между ними одного треугольника равны соответственно двум углам и стороне между ними другого, а такие треугольники, как знаем (п. 47), равны. Также можно найти равенство ∆OBC = ∆ODA. Из равенства треугольников OAB и OCD следует, что OA = OC (против равных углов 2 и 4) и BO = OD (против равных углов 1 и 3), т. е. диагонали в точке O разделили друг друга на 2 равных отрезка или пополам. Этот результат можно выразить словами:
Диагонали параллелограмма делят друг друга пополам.
Точка O, в которой AC и BD делятся пополам, называется серединою отрезка AC и серединою отрезка BD.
57. При помощи построения параллелограмма мы можем теперь каждый данный отрезок разделить пополам, или, другими словами, найти середину этого отрезка.
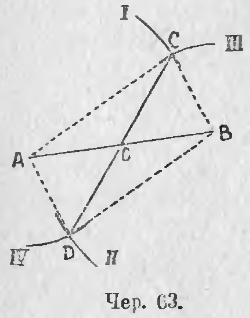
Пусть дан отрезок AB (чер. 63); требуется найти его середину. Примем AB за одну из диагоналей параллелограмма, который и надо построить для решения задачи. Такая задача была уже предложена (зад. 6 п. 54); дадим здесь ее решение. Прежде всего мы замечаем, что у нас уже имеются две противоположных вершины искомого параллелограмма A и B, – другие две вершины должны лежать где-либо по разные стороны прямой AB. Так как стороны параллелограмма нам не даны, то мы можем взять произвольный отрезок, которому должна равняться каждая из одной пары параллельных сторон параллелограмма, и радиусом, равным этому отрезку, опишем дугу I, принимая за центр точку A, и дугу II, принимая за центр точку B. Также, выбрав произвольный отрезок для другой пары сторон параллелограмма (впрочем, он должен быть больше разности между первым отрезком и диагональю AB и меньше их суммы, – иначе окружности не пересекутся, см. п. 25), мы радиусами, разными этому отрезку, опишем дугу III, принимая B за центр, и дугу IV, принимая A за центр, – точка C, где пересекаются дуги I и III, и точка D, где пересекаются дуги II и IV, должны служить другими двумя вершинами параллелограмма. Соединив их прямыми с точками A и B, получим искомый параллелограмм, диагональю которого служит данный отрезок AB. Ясно, что таких параллелограммов можно построить бесчисленное множество, так как выбор сторон AC и BC зависит от нас.
Нам важна вторая диагональ этого построенного параллелограмма, диагональ CD; построив ее, мы, на основании предыдущего п., можем утверждать, что задача решена, что точка O, где CD пересекается с AB, есть середина AB.
Заметим, что нет надобности строить стороны параллелограмма AC, CB, BD и DA, – нужно лишь построить его вторую диагональ CD.
58. Задача. Построить параллелограмм по его диагоналям и одной стороне.
Пусть даны отрезки a, b и c (чер. 64); требуется построить такой параллелограмм, чтобы отрезки a и b служили его диагоналями и отрезок c одною из его сторон.
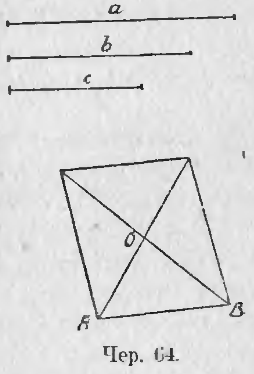
Чтобы разобраться в этой задаче, начертим (хотя бы от руки) параллелограмм и будем считать, что его диагонали и одна из сторон (напр., отмеченная на чертеже черточкою) нам известны. Зная свойство диагоналей (п. 56), мы придем к заключению, что мы можем построить ∆AOB, в котором нам все три стороны известны: AB данная, AO и OB суть половины данных диагоналей. Поэтому построение должно быть выполнено в таком порядке: 1) надо, согласно п. 57, разделить пополам каждую из данных диагоналей a и b, 2) построить ∆, у которого сторонами служат найденные половины диагоналей и данная сторона параллелограмма c (п. 38) и 3) дополнить построенный треугольник до параллелограмма, для чего надо продолжить его 2 стороны, которые являются половинами данных диагоналей, отложить на продолжениях опять половины диагоналей и концы этих отрезков соединить с концами стороны c.
Иногда данные могут быть таковы, что задача невозможна, – это можно узнать при выполнении 2-го построения.
59. Можно ускорить решение задачи деления данного отрезка пополам, для чего следует описывать дуги из концов данного отрезка не различными, а одинаковыми радиусами.
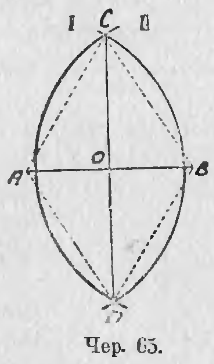
Пусть требуется отрезок AB (чер. 65) разделить пополам; для этого, принимая последовательно точки A и B за центры, построим две окружности I и II одинаковыми радиусами и их точки пересечения C и D соединим прямою, – точка O, где CD пересекает AB, и является серединою отрезка AB. Можно, конечно, строить не полные окружности, а лишь их дуги, достаточные для определения положения точек C и D. Для того, чтобы эти окружности пересеклись, необходимо, чтобы их общий радиус был больше половины отрезка AB.
Если построить самый параллелограмм, то увидим, что все его стороны равны между собою: AC = CB = BD = DA, так как окружности описывались одинаковыми радиусами. Следовательно, здесь мы построили особый параллелограмм, все стороны которого равны между собою, – такой параллелограмм называется ромбом.
Упражнение. Разделить данный отрезок на 4, на 8 и т. д. равных частей.
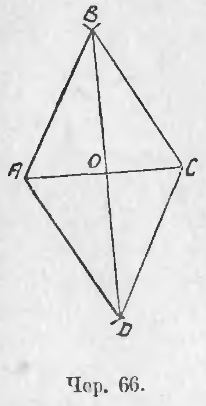
60. Изучение ромба. Для того, чтобы параллелограмм обратился в ромб, достаточно, чтобы две его соседние стороны были равны. Если, напр., построен параллелограмм ABCD (чер. 66) так, что AB = BC, то, на основании свойств сторон параллелограмма, имеем CD = AB и AD = BC, откуда следует, что AB = BC = CD = DA, т. е., что этот параллелограмм есть ромб.
Упражнения.
- Строить различные ромбы на данной стороне.
- Строить различные ромбы на данном угле.
- Построить ромб по данной его стороне и углу.
- Строить различные ромбы на данной диагонали.
- Построить ромб по его стороне и диагонали.
То обстоятельство, что ромб есть особенный параллелограмм (параллелограмм с равными сторонами), дает основание думать, что эта особенность должна отразиться и на других частях ромба. Оказывается, что она отражается на его диагоналях.
Пусть построен ромб ABCD (чер. 66) и его диагонали AC и BD. Тогда прежде всего мы уже знаем, что каждая диагональ делится в точке O пополам, так как ромб есть тоже параллелограмм (п. 56). Теперь надо воспользоваться особенностью ромба: в ромбе все стороны равны, но мы уже знаем, что в параллелограмме противоположные стороны равны, и мы этим воспользовались в п. 56, где нашли, что, благодаря этому, точка O есть середина каждой диагонали; теперь, следовательно, надо обратить внимание на равенство двух соседних сторон, т. е., напр., на равенство AB = BC; возникает мысль: не повлечет ли это равенство за собою следствием равенство двух треугольников, сторонами которых служат AB и BC, т. е. ∆AOB и ∆BOC? Рассмотрим эти треугольники: у них 1) сторона BO общая, 2) AB = BC, как стороны ромба, и 3) AO = OC, так как точка O есть середина диагонали AC. Мы знаем, что если три стороны одного треугольника равны соответственно трем сторонам другого, то такие треугольники равны; следовательно, ∆AOB = ∆OBC. Отсюда следует: 1) ∠ABO = ∠OBC (эти углы расположены против равных сторон AO и OC) и 2) ∠AOB = ∠BOC (против равных сторон AB и BC). Первое равенство углов указывает, что ∠ABC ромба разделен диагональю BD на два равных угла. Если бы мы рассмотрели треугольники OBC и OCD, то также нашли бы, что ∠BCD ромба делится диагональю CA на два равных угла; то же можно получить и про остальные два угла. Поэтому имеем первое свойство диагоналей ромба:
1) Диагонали ромба делят его углы пополам.
Рассматривая 2-е из найденных равенств, т. е. равенство ∠AOB = ∠BOC, видим, что здесь выпрямленный угол AOC делится также диагональю BD пополам; не трудно также увидать, что все 4 угла при точке O равны между собою, т. е. ∠AOB = ∠BOC = ∠COD = ∠DOA (это можно увидать, напр., из того, что ∠AOD = ∠BOC, как вертикальные, и по той же причине ∠COD = ∠BOA, – следовательно, все 4 угла равны между собою), причем каждый из них получился от разделения на две равных части выпрямленного угла (напр., ∠COD получился от разделения на 2 равных части выпрямленного угла BOD и т. д.). Принято называть углы, получающиеся от разделения выпрямленного угла на две равных части, прямыми углами; следовательно, у нас получились прямые углы: ∠AOB, ∠BOC, ∠COD, ∠DOA. Коротко выражают ту же мысль словами: прямым углом называется половина выпрямленного угла.
Вот необходимые нам свойства прямых углов:
a) Все прямые углы равны между собою.
Это следует из того, что все выпрямленные углы равны между собою, а, следовательно, и их половины (прямые углы) тоже равны.
b) Если один из четырех углов, образуемых двумя пересекающимися прямыми, прямой, то и остальные три угла прямые.
В самом деле, если при точке пересечения прямых a и b (чер. 67) получились углы 1, 2, 3 и 4, из которых, напр., ∠1 прямой, то и ∠2 прямой, так как ∠1 и ∠2 вместе составляют выпрямленный угол, но ∠3 = ∠1, как вертикальные, следовательно, и ∠3 прямой, так же и ∠4 прямой, потому что он равен ∠2.
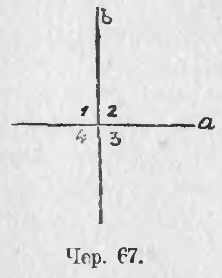
Две прямые линии, которые, пересекаясь, образуют прямые углы, называются перпендикулярными прямыми (иногда взаимно-перпендикулярными).
Поэтому второе свойство диагоналей ромба можно выразить в такой форме:
2) Диагонали ромба взаимно перпендикулярны.
61. Пользуясь первым свойством диагоналей ромба, мы можем всякий данный угол разделить пополам:
Пусть дан ∠A (чер. 68); требуется разделить его пополам. Для этого придется построить такой ромб, чтобы ∠A был его углом и построить диагональ этого ромба чрез точку A.
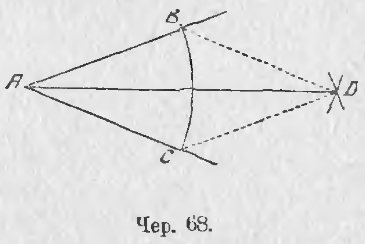
Отложим на сторонах угла A два равных (но произвольных) отрезка AB = AC; тогда у нас будут построены 3 вершины ромба A, B и C, четвертая же вершина должна лежать где-то внутри угла A. Затем, принимая последовательно точки B и C за центры, построим круги (или только их дуги, достаточные для определения четвертой вершины ромба) радиусами, равными отрезкам AB и AC; точка пересечения этих кругов, точка D, расположенная внутри угла A, и дает нам четвертую вершину ромба. Соединив ее с B и C прямыми (впрочем, для деления угла пополам это лишнее, и на первый раз нужно лишь для того, чтобы увидать, что получился ромб), получим ромб ABDC; построив его диагональ AD, разделим угол A на два равных угла на ∠BAD и ∠DAC.
Луч, делящий угол пополам, называется биссектором этого угла; AD есть биссектор угла BAC (чер. 68).
Ясно, что всякий угол может быть вышеописанным способом разделен пополам, или у всякого угла есть биссектор.
Если вообразить, что построенный биссектор AD угла BAC вращается около вершины угла A в ту или иную сторону, то равенство углов BAD и DAC нарушается: один угол увеличивается, а другой уменьшается. Поэтому:
Всякий угол может быть разделен пополам лишь одним способом.
Или:
У всякого угла имеется лишь один биссектор.
62. Упражнения.
- Построить ромб по его углу и диагонали, проходящей через вершину этого угла.
Надо построить данный угол, его биссектор, на нем отложить данную диагональ и чрез конец ее построить прямые, параллельные сторонам угла. - Построить четырехугольник по его двум противоположным углам и по диагонали, соединяющей вершины этих углов, причем четырехугольник должен быть симметричным относительно данной диагонали.
Как располагается другая диагональ этого четырехугольника относительно данной? - Разделить данный угол на 4, на 8 и т. д. равных частей.
- Построить биссекторы двух смежных углов. Показать, что они перпендикуляры между собою.
63. Задача. Построить на данной прямой при данной ее точке прямой угол.
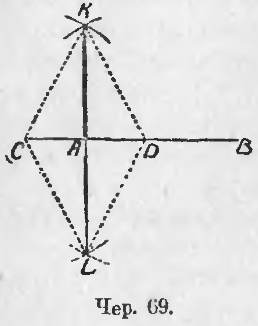
Раз мы умеем строить ромб, то мы умеем, вообще говоря, строить прямые углы. Для решения задачи этого п. Надо расположить ромб так, чтобы точка пересечения его диагоналей совпала с данною точкою A (чер. 69) и одна диагональ шла по данной прямой AB. Для этого от точки A в обе стороны отложим на данной прямой равные (но произвольные) отрезки AC = AD; тогда точки C и D можно принять за две вершины ромба. Для построения двух других вершин надо, принимая последовательно точки C и D за центры, построить две окружности (или их дуги, достаточные для получения точек пересечения) одним и тем же радиусом, большим, чем отрезок AC (иначе окружности не пересекутся). Соединив прямыми точки пересечения наших окружностей K и L с точками C и D, получим ромб CKDL; его диагональ KL должна пройти чрез середину диагонали CD, т. е. чрез точку A; построив эту диагональ KL, получим 4 прямых угла (п. 60).
Важно ускорить и упростить это построение:
1) Нет надобности строить стороны ромба, 2) можно построить лишь одну точку пересечения окружностей, напр., точку K, и тогда , построив отрезок KA, получим два прямых угла; если его продолжить, то получим еще два прямых угла. На чертеже изображены пунктиром те линии, построение которых излишне.
64. Задача. Построить параллелограмм с прямым углом.
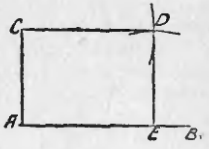
Строим произвольную прямую AB и выбираем на ней произвольную точку A (чер. 70), при которой строим (п. 63) прямой угол; на стороне AC этого прямого угла выбираем произвольную точку C и на прямой AB точку E. Затем, принимая последовательно точки C и E за центры, строим две окружности (или дуги): первую (центр C) радиусом, равным отрезку AE, и второю (центр E) радиусом, равным отрезку AC; точка пересечения этих окружностей точка D, лежащая по ту же сторону прямой AB, как и точка C и должна служить четвертою вершиною этого параллелограмма. Построив, наконец, прямые CD и DE, получим искомый параллелограмм ACDE, у которого ∠A прямой (сравнить это построение с п. 53).
Рассмотрим остальные углы этого параллелограмма: 1) мы знаем, что ∠D = ∠A, как противоположные углы параллелограмма (п. 51), следовательно, угол D тоже прямой; 2) затем знаем, что ∠C + ∠A = выпрямленному углу, как соседние углы параллелограмма (п. 51, 1), но ∠A прямой, т. е. равен половине выпрямленного угла, следовательно, и ∠C равен половине выпрямленного, т.е. тоже есть прямой угол, затем ∠E = ∠C и, следовательно, ∠E тоже прямой. Итак, оказалось:
Если в параллелограмме один угол прямой, то и остальные углы прямые.
Такой параллелограмм с прямыми углами называется прямоугольником.
65. Так как прямоугольник есть особенный параллелограмм, то эта особенность должна отразиться, как и в ромбе, на его диагоналях.
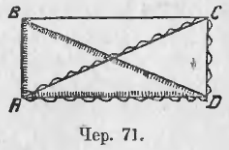
Пусть построен прямоугольник ABCD (чер. 71) и построены его диагонали AC и BD. Конечно, основное свойство диагоналей параллелограмма остаётся и здесь: диагонали делят друг друга пополам. Но нам надо открыть какую-либо особенность диагоналей, зависящую от того, что теперь у нашего параллелограмма все углы прямые. Рассмотрим пару треугольников, в каждый из которых входил бы один из прямых углов, и важно, чтобы входили два соседних прямых угла, напр., ∠A и ∠D (соседние углы ведь вообще в параллелограмме не равны, а противоположные всегда равны). Такими треугольниками являются ∆ABD (∠A прямой) и ∆ACD (∠D прямой). У этих треугольников сторона AD общая, затем сторона AB первого равна стороне CD второго и между ними равные углы, так как мы знаем, что прямые углы равны между собою (п. 60, а). Следовательно, две стороны (AD и AB) и угол между ними (прямой ∠A) одного треугольника равны соответственно двум сторонам (AD и CD) и углу между ними (прямой ∠D) другого треугольника, а мы знаем, что такие треугольники равны. Отсюда выводим, что AC = BD, т. е. оказывается, что диагонали равны между собою.
Итак:
Диагонали прямоугольников равны между между собою.
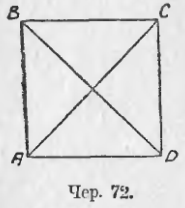
66. Наконец, можно построить такой прямоугольник, чтобы у него все стороны были равны (построение ясно: строим прямой угол A (чер. 72) и на его сторонах откладываем равные отрезки AB = AD, затем обычным приёмом находим четвертую вершину C). Такой параллелограмм является в одно и то же время и прямоугольником (у него все углы прямые, так как один угол прямой) и ромбом (у него все стороны равны, так как две соседних равны), - она называется квадратом. Его диагонали должны обладать свойствами диагоналей и параллелограмма, и ромба, и прямоугольника, т. е.:
Диагонали квадрата взаимно делятся пополам, делят углы квадрата пополам и взаимно перпендикулярны и, наконец, равны между собою.
67. Упражнения.
- Построить прямоугольник по его сторонам.
- Построить прямоугольник по диагонали и одной из его сторон.
- Построить квадрат по его стороне.
- Построить квадрат по его диагонали.
