77. Нам уже приходилось строить четырехугольники (п. 50). Теперь расширим это построение. Пусть даны 4 точки: A, B, C и D [чер. 84 (I)]; построим всевозможные прямые соединяющие попарно эти 4 точки – мы полагаем, что никакие 3 из данных точек не расположены на одной прямой. Таких прямых можно всего построить 6 (из каждой точки к трем остальным идут 3 прямых, так как точек 4, то всего прямых 3 * 4 = 12, но каждая прямая здесь считалась два раза, напр., прямая AC: один раз мы ее считали идущею от A к C и другой раз – от C к A; поэтому различных прямых должно быть (4 * 3) / 2 = 6). Полученная фигура состоит из 4 точек и 6 соединяющих их попарно прямых, – она называется полным четырехугольником. Каждая из данных четырех точек называется его вершиною, а каждая входящая в его состав прямая – его стороною: у полного 4-угольника 4 вершины и 6 сторон.

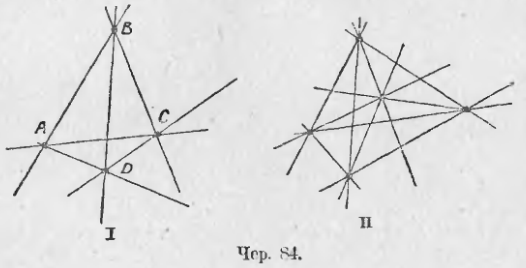
Если мы возьмем 5 точек (чер. 84 – II), чтобы никакие 3 из них не лежали на одной прямой, и соединим их попарно прямыми, то получим полный 5-угольник; у него 5 вершин и 10 сторон. У полного 6-угольника 6 вершин и 15 сторон и т. д.

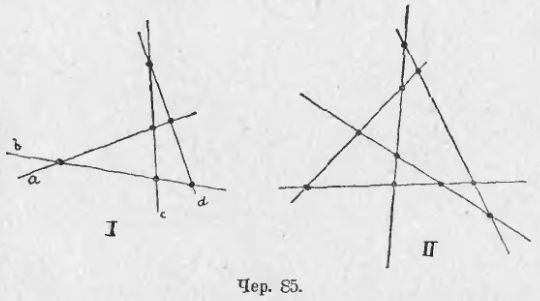
Наоборот, можно построить 4 прямых a, b, c и d (чер. 85 – I) так, чтобы никакие три из них не проходили чрез одну точку, и найти их точки пересечения. Предположим, что среди прямых a, b, c и d нет ни одной пары параллельных; тогда каждая прямая с тремя остальными пересекается в трех точках, а всего точек пересечения 3 * 4 = 12, но здесь каждая точка считалась 2 раза: один раз, напр., от пересечения прямой a с прямой b, а другой раз от пересечения прямой b с прямой a; поэтому число различных точек пересечения должно быть 4 * 3 / 2 = 6. Полученная фигура, состоящая из 4 прямых и 6 точек их пересечения, называется полным четырехсторонником; каждая прямая называется его стороною и каждая точка – его вершиною. У четырехсторонника 4 стороны и 6 вершин. Если такое же построение выполнить с 5 прямыми, то получим полный пятисторонник (чер. 85 – II). У него, если положим, что среди 5 прямых нет ни одной пары параллельных, 5 сторон и 10 вершин. У полного шестисторонника (с тою же оговоркою относительно прямых) 6 сторон и 15 вершин и т. д.

78. Возьмем опять несколько точек и соединим их попарно прямыми, но не каждую с каждой, а, наметив предварительно их порядок, каждую с последующей (последнюю опять с первой). Построенная таким образом фигура носит название: простой многоугольник – на чер. 86 даны изображения простых 5-угольника и 6-угольника.

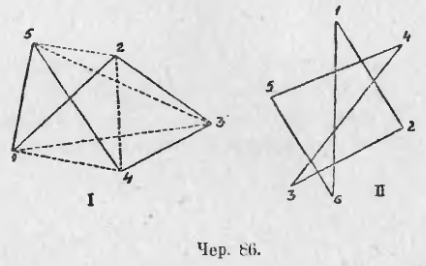
Порядок взятых точек на чертеже обозначен цифрами: здесь надо, чтобы три соседних точки не лежали на одной прямой. Каждая точка, входящая в состав простого многоугольника, называется его вершиною и каждая прямая – его стороною (мы можем здесь, как это было и в треугольнике, понимать под этим именем лишь отрезок прямой, соединяющий две соседних вершины многоугольника). Не трудно увидать, что в простом многоугольнике столько же сторон, сколь и вершин. Если соединить прямою две несоседних вершины, то полученная прямая (или ее отрезок, заключенный между взятыми вершинами) называется диагональю этого многоугольника. На чер. 86 (I) построено пунктиром 5 диагоналей простого пятиугольника. В простом шестиугольнике можно построить 9 диагоналей (на чер. 86 – II они не построены). Так как у простого многоугольника сторон столько же, сколько и вершин, то их можно еще называть простыми многосторонниками (простой пятисторонник и т. п.). На чер. 87 и 88 даны еще различные виды простых многоугольников.

79. В курсе элементарной геометрии рассматриваются только простые многоугольники, а потому их часто называют одним словом многоугольники. При построении простых многоугольников могут быть два случая: 1) стороны многоугольника, понимая под этим именем отрезки прямых между двумя вершинами, пересекают друг друга (см. чер. 86) и 2) не пересекают друг друга (чер. 87 и 88). Между этими двумя случаями существенная разница. В то время, как во втором случае мы видим, что многоугольник выделяет из плоскости ее определенную часть, которая называется площадью этого многоугольника, в первом случае мы видим, что там выделяется несколько частей – особенно это заметно на чер. 86, II, – причем можно выделить даже иногда такие две части, что одна из них частию наложена на другую; здесь, следовательно, мы не видим сразу площадь, ограничиваемую этим многоугольником. Поэтому мы будем называть многоугольники, подходящие под второй случай (чер. 87 и 88), имеющими площадь, и многоугольники, подходящие под первый случай (чер. 86) – не имеющими площади (их еще называют звездчатыми).

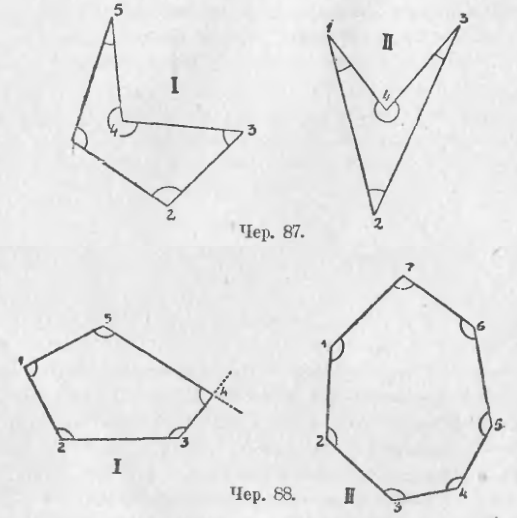
Следует заметить, что, сделав несколько условий, позволяющих части плоскости считать то положительными, то отрицательными, можно считать, что всякий многоугольник имеет площадь. Вопрос о площади звездчатых многоугольников не входит в курс элементарной геометрии.

Часто еще рассматривают так называемый периметр многоугольника; этим именем называют сумму всех сторон многоугольника.

80. В элементарной геометрии почти исключительно рассматриваются многоугольники, имеющие площадь. При каждой вершине такого многоугольника получаются углы, по 4 угла при каждой, если под сторонами многоугольника понимать бесконечные прямые (напр., см. углы при вершине 4 пятиугольника I чер. 88). Один из этих углов, внутренняя область которого захватывает площадь многоугольника, называется внутренним; при каждой вершине многоугольника получается по одному внутреннему углу (на чер. 87 и 88 внутренние углы отмечены дугами).

Здесь опять возникает разделение многоугольников, имеющих площадь, на два класса: 1) каждый внутренний угол многоугольника меньше выпрямленного угла, – такие многоугольники называются выпуклыми (чер. 88); 2) может случиться, что один или несколько внутренних углов больше выпрямленного (на чер. 87 углы при вершинах 4 в обоих многоугольниках), – такие многоугольники называются невыпуклыми.

Выпуклый многоугольник обладает свойством, что все его вершины расположены по одну сторону от каждой его стороны (понимая под этим именем бесконечную прямую). Невыпуклый многоугольник этим свойством не обладает.

В дальнейшем нам придется иметь дело, главным образом, с выпуклыми многоугольниками.

81. Первою нашей задачею о многоугольниках является нахождение суммы внутренних углов многоугольника.

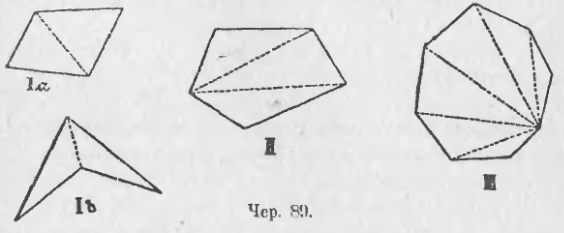
Если мы возьмем какой-либо четырехугольник, имеющий площадь [чер. 89, I (a) или I (b)], и построим одну из его диагоналей – в случае I (a) безразлично какую, а в случае I (b), ту, которая расположена на площади этого 4-угольника (внутри его), то получим 2 треугольника. Сумма внутренних углов каждого треугольника 2d, следовательно, сумма внутренних углов 4-угольника = 2d * 2 = 4d. Если возьмем какой-либо 5-угольник и построим две диагонали, идущие из одной его вершины (чер. 89, II), то получим 3 треугольника; так как сумма внутренних углов треугольника = 2d, то сумма внутренних углов 5-угольника = 2d * 3 = 6d; также для 6-угольника получим 4 треугольника и, следовательно, сумма его внутренних углов = 2d * 4 = 8d и т. д. Если возьмем, напр., 11-угольник, то после построения диагоналей получим 9 треугольников. Сумма внутренних углов 11-угольника = 2d * 9 = 18d. Вообще, если возьмем n-угольник, то после построения диагоналей из одной его вершины получим (n – 2) треугольников и, следовательно, сумма внутренних углов этого многоугольника выразится формулою:

2d(n – 2)

где n выражает число сторон или вершин этого многоугольника.

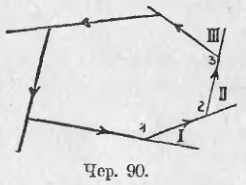
82. Вторым вопросом будет вопрос о сумме внешних углов многоугольника. Под названием «внешний угол» можно понимать, как это мы уже и делали для треугольника, угол, составленный продолжением одной стороны многоугольника со следующею стороною (∠I, ∠II и т. д. на чер. 90). Станем идти по сторонам этого многоугольника, который будем считать выпуклым, напр., по направлению, указанному стрелками, и каждую из сторон продолжать в том же направлении. Тогда получим ряд внешних углов: ∠I, ∠II и т. д. Рассмотрим сначала одну пару углов: внутренний и внешний при общей вершине, напр., ∠1 и ∠I; тогда мы видим, что сумма их есть выпрямленный угол, т. е.

∠1 + ∠I = 2d.

Также найдем при другой вершине: ∠2 + ∠II = 2d и т. д. Если положим, что всего вершин в многоугольнике было n, таких пар углов также n, и следовательно:

(Сумма внутренних углов) + (сумма внешних углов) = 2d * n

Но мы знаем, что

сумма внутренних углов = 2d(n – 2).

Следовательно:

Сумма внешних углов = 2dn – 2d(n – 2) = 2dn – 2dn + 4d = 4d

т. е. сумма внешних углов выпуклого многоугольника не зависит от числа сторон (или вершин) этого многоугольника и всегда равна 4d.

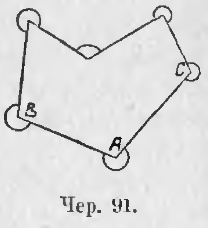
83. Добавление. Можно название «внешний угол» понимать и в другом смысле. Пусть имеем какой-либо многоугольник (чер. 91), имеющий площадь, хотя бы и не выпуклый. Тогда под внешним углом можно понимать угол, составленный сторонами многоугольника, а не их продолжениями, как и внутренний угол, напр., ∠BAC, но за внутреннюю его область принять ту часть плоскости, выделяемую сторонами этого угла, которая не заключает в себя площади этого многоугольника. Внутренняя область каждого из этих углов отмечена на чертеже дугою. Тогда каждый такой угол, вместе с соответствующим ему внутренним углом, составляет 2 выпрямленных угла или 4d, напр., внутренний ∠BAC + внешний ∠BAC = 4d.

Если сторон у многоугольника n, то сумма всех внутренних и сумма всех внешних = 4d*n, а, следовательно, сумма внешних углов = 4dn – 2d(n – 2) = 4dn – 2dn + 4d = 2dn + 4d = 2d(n + 2).

84. Упражнения.

1. Построить полный шестиугольник. Сколько у него сторон?
2. Построить полный шестисторонник так, чтобы у него не было параллельных сторон. Сколько у него вершин?
3. Найти общую формулу для числа сторон полного n-угольника и для числа вершин полного n-сторонника (полагая, что у последнего нет параллельных сторон).
4. Сколько диагоналей можно построить из одной вершины простого n-угольника?
5. Сколько всего диагоналей у простого n-угольника?
6. Выразить в частях прямого угла каждый внутренний угол выпуклого пятиугольника, если у него все углы равны между собою.
7. Выразить для пятиугольника предыдущей задачи каждый внешний угол в частях прямого угла.
8. В равнобедренном треугольнике каждый угол при основании = ¾d. Найти (в частях прямого угла) его угол при вершине.
9. В равнобедренном треугольнике угол при вершине = 5/8 d. Найти его угол при основании.
10. В выпуклом четырехугольнике противоположные углы попарно равны между собою. Выяснить, что такой четырехугольник есть параллелограмм.