152. До сих пор мы занимались сравнением отрезков, углов и дуг круга. Теперь обратим внимание на то, что мы умеем строить многоугольники, выделяющие из плоскости ее определенную часть, многоугольники, имеющие площадь. Возникает потребность установить возможность узнавать, когда две площади равны, или когда одна из них больше другой.
Площадью вообще называется определенная, ограниченная со всех сторон, часть плоскости.
Если две площади совпадают при наложении, то они, подобно отрезкам и углам, признаются нами равными. Если два многоугольника равны (т. е. совпадают при наложении), то и площади их равны.
Мы легко можем составить представление о возможности находить сумму и разность площадей. Пусть имеем два многоугольника (чер. 158) I и II. Мы можем построить многоугольник BCDE, равный II так, чтобы одна его сторона пошла по стороне BF многоугольника ABFGH, который равен многоугольнику I. Тогда получим новый многоугольник ABCDEFGH, площадь которого слагается из площадей I и II многоугольников, то есть
площ. ABCDEFGH = площ. I + площ. II
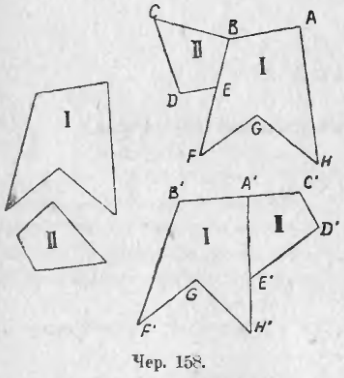
Мы можем выполнить сложение этих же двух площадей иначе и придем. Напр., к многоугольнику A'B'F'G'H'E'D'C', о котором также имеем:
площ. A'B'F'G'H'E'D'C' = площ. I + площ. II
Для того, чтобы получилось согласи с привычною для нас мыслью, что сложение ведет лишь к одному результату, мы должны признать, что два полученные результата одинаковы, то есть:
площадь ABCDEFGH = площадь A'B'F'G'H'E'D'C'
Таким образом, является возможность строить многоугольники, не равные между собою (многоугольник A'B'F'G'H'E'D'C' вообще не равен многоугольнику ABCDEFGH, так как при наложении они, вообще говоря, не могут совпасть: например, может случиться, что у одного из них сторон меньше, чем у другого — на чертеже, напр., ∠C'A'B' может оказаться выпрямленным), но площади которых мы признаем равными.
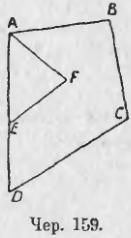
Не трудно также установить возможность вычитания площадей; напр., многоугольник ABCDEFA (чер. 159) имеет площадь, равную разности площадей 4-угольника ABCDA и треугольника AFE. Ясно, что вычитание можно выполнять так же, как и сложение, разными способами и что результаты вычитания мы должны, каким бы способом мы это вычитание ни выполнили, считать одинаковыми. Поэтому мы можем установить:
Две площади, ограниченные прямыми линиями, считаются равными не только тогда, когда они при наложении совмещаются, но и тогда, если каждая их них является суммою или разностью двух (или нескольких) площадей, совпадающих попарно при наложении.
Мы рассматриваем только площади, ограниченные прямыми линиями.
Если же одна площадь слагается из частей так, что из них не только можно составить другую площадь, но и остаются лишние части, то первая площадь больше второй.
Два многоугольника, не равные между собою, но имеющие равные площади, называются равновеликими. На чер. 158 мы получили многоугольник A'B'F'G'H'E'D'C' равновеликий многоугольнику ABCDEFGH.
153. Рассмотрим один пример равновеликих многоугольников, важный для последующего.
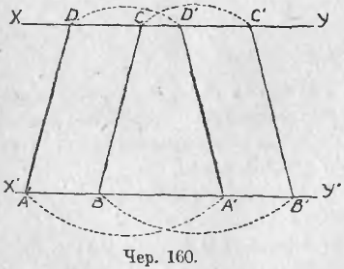
Построим два параллелограмма с одинаковыми основаниями и высотами. Это построение легко выполнить: Строим две параллельных прямых XY и X'Y' (чер. 160) и на них отрезки AB = A'B' = DC = D'C'; построив затем отрезки AD, BC, A'D' и B'C', получим два параллелограмма ABCD и A'B'C'D' с равными основаниями (AB = A'B') и с равными высотами, так как прямые XY и X'Y' параллельны (п. 55).
Рассмотрим 2 трапеции AA'D'D и BB'C'C. Так как AB = A'B', то AA' = BB' и также DD' = CC', т. е. параллельные стороны наших трапеций соответственно равны; непараллельные их стороны также равны: AD = BC и A'D' = B'C'. Кроме того, не трудно убедиться в равенстве соответствующих углов ∠DAA' = ∠CBB', ∠AA'D' = ∠BB'C' и т. д., как соответственных при параллельных. Если передвинуть вторую трапецию так, чтобы точка B попала в A и сторона BB' пошла бы по AA', то в силу равенства сторон и углов нетрудно убедиться, что наши 2 трапеции равны. Далее мы видим:
площ. ABCD = площ. AA'D'D – площ. BA'D'C
площ. A'B'C'D' = площ. BB'C'C – площ. BA'D'C,
т. е. площадь каждого параллелограмма является разностью двух совпадающих при наложении площадей, а поэтому
площ. ABCD = площ. A'B'C'D'.
Более наглядное объяснение: для получения площади параллелограмма ABCD надо от площади трапеции AA'D'D отрезать площадь BA'D'C, а для получения площади параллелограмма A'B'C'D' надо от площади трапеции BB'C'C отрезать ту же площадь BA'D'C; оба раза от равных площадей отрезать одну и ту же площадь, – поэтому и остатки равны.
Вот другой способ для выяснения равенства площадей параллелограммов, имеющих равные основания и высоты.
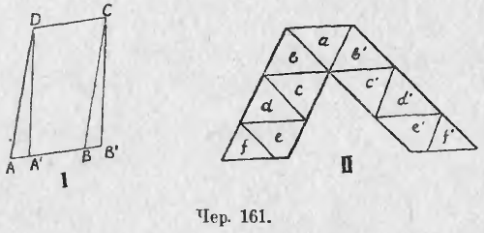
Построим два параллелограмма ABCD и A'B'CD (чер. 161 — I) так, чтобы их равные (верхние, например) основания совпали (CD — их общее верхнее основание). Вследствие равенства их высот, противоположные стороны AB и A'B' располагаются на одной прямой. Тогда видим, что ∆ADA' = ∆BCB' (так как AD = BC, A'D = B'C и ∠ADA' = ∠BCB') и что
площ. ABCD = площ. A'BCD + площ. AA'D
площ. A'B'CD = площ. A'BCD + площ. BCB'.
Слагаемые наших сумм попарно равны, отсюда заключаем, что
площ. ABCD = площ. A'B'CD.
То же самое можно выразить образно: отрезав от площади ABCD площадь ADA' и приставив отрезанную часть с другой стороны в положение BCB' (ведь ∆BCB' = ∆ADA'), получим площадь параллелограмма A'B'CD.
Но иногда одним разрезом обойтись нельзя. На чер. 161 (II) дан более сложный случай, где придется площадь левого параллелограмма разрезать на части a, b, c, d, e и f и перенести их в положения b', c', d', e' и f' (a останется на месте), – тогда составится площадь правого параллелограмма. Разрезать площадь одного параллелограмма надо по прямым параллельным сторонам другого параллелограмма (параллелограммы располагаются так, как на чер. II).
Рекомендуется вырезать два параллелограмма с равными основаниями и равными высотами из разноцветной бумаги и разрезать площадь одного на такие куски, чтобы из них составить площадь другого.
Не трудно убедиться, что если основания у двух параллелограммов равны, а высоты нет, то площадь того параллелограмма больше, у которого больше высота.
154. Прямоугольник представляет частный вид параллелограмма. Поэтому:
Параллелограмм равновелик прямоугольнику, имеющему такие же основание и высоту.
Превращение параллелограмма в равновеликий ему прямоугольник можно выполнить так: из вершин D и C параллелограмма ABCD (чер. 162 — I и II) опускаем перпендикуляры DE и CF на сторону AB. Тогда получим прямоугольник DEFC, равновеликий, в силу предыдущего, данному параллелограмму.
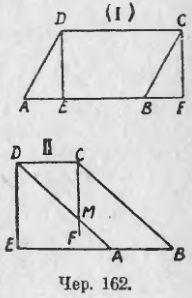
Полезно увидать равновеликость параллелограмма прямоугольнику непосредственно, не ссылаясь на предыдущий п.; напр., для случая, данного на чер. II, имеем: после построения DE ⊥ EB к площади ABCD мы приложили еще площадь ∆ADE, после построения CF ⊥ AF мы из площади EBCD вычли площадь ∆BCF, но ∆BCF = ∆ADE, следовательно, полученная после вычитания площадь EDCF равна данной площади ABCD.
155. В виде упражнений разберем следующие случаи равновеликости. Пусть на отрезке a + b (чер. 163) построен квадрат и пусть построены еще прямые, соединяющие точки, где граничат слагаемые отрезки. Тогда видим, что площадь всего квадрата слагается из четырех частей: 1) площади квадрата со стороною a, 2) площади квадрата со стороною b и 3) из площадей двух прямоугольников со сторонами a и b. Поэтому имеем:
Площ. (a + b, a + b) = площ. (a, a) + площ. (b, b) + 2 площ. (a, b).
Здесь обозначения: (a + b, a + b), (a, b) и т. д. Выражают прямоугольники, стороны которого суть в 1-м a + b и a + b, а во 2-м a и b.
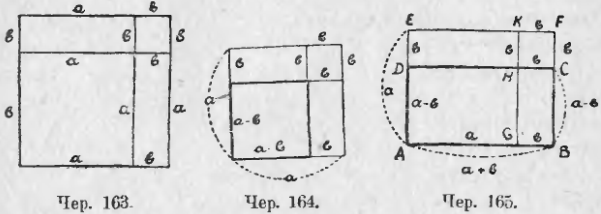
Также из чертежа 164 увидим:
Площ. (a – b, a – b) = площ. (a, a) + площ. (b, b) – 2 площ. (a, b).
Из чертежа 165 увидим:
Площ. ABCD = площ. AGKE + площ. GKFB – площ. DEKH – площ. HKFC
или площ. (a + b, a – b) = площ. (a, a) + площ. (a, b) – площ. (a, b) – площ. (b, b)
или площ. (a + b, a – b) = площ. (a, a) – площ. (b, b).
Эти зависимости могут служить иллюстрациями известных алгебраических формул.
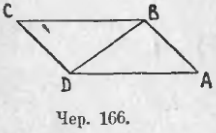
156. Если построим диагональ BD параллелограмма ABCD (чер. 166), то получим ∆ABD, имеющий такие же основания и высоту, как и параллелограмм. Кроме того, известно, что ∆ABD = ∆DBC. Поэтому имеем:
Площадь треугольника равна половине площади параллелограмма, имеющего такие же основание и высоту.
Или сокращенно:
Треугольник равновелик половине параллелограмма, имеющего такие же основание и высоту.
Из сравнения только что полученного результата с тем, который мы нашли в п. 153, можем заключить:
Треугольники, имеющие равные основания и равные высоты, равновелики.
Добавим еще: если у двух параллелограммов одинаковые основания, но разные высоты, то площадь того параллелограмма больше, у которого высота больше, – это ясно из того, что параллелограмм с меньшею высотою можно превратить в равновеликий ему, площадь которого занимает лишь часть площади другого параллелограмма. Отсюда заключаем, что если у двух треугольников одинаковые основания, но разные высоты, то площадь того треугольника больше, у которого высота больше.
Добавление. Любой треугольник можно превратить в равновеликий ему прямоугольник.
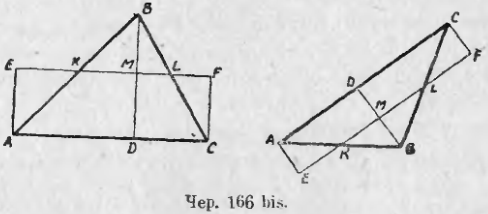
Пусть имеем ∆ABC (чер. 166 bis, где даны 2 варианта: слева дан ∆ со всеми острыми углами, а справа ∆ с тупым углом). Если у треугольника все углы острые, то построим любую его высоту BD, а если у треугольника один угол тупой, напр., ∠B (в ∆ABC справа), то построим высоту ВD именно из вершины этого тупого угла (в таком случае всегда высота BD идет внутри треугольника). Разделим затем высоту BD пополам в точке M и построим через M прямую EF || AC, а через точки A и C прямые AE ⊥ AC и CF ⊥ AC. Тогда ясно: 1) ∆KBM = ∆KAE (точка K есть точка пересечения AB и EF), 2) ∆MBL = ∆FCL (точка L есть точка пересечения BC и EF), откуда следует, что площ. AEFC = площ. ∆ABC.
157. Построим геометрическое место вершин равновеликих треугольников, имеющих общее основание.
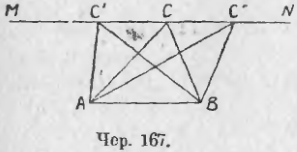
Пусть имеем ∆ACB (чер. 167). Чтобы другой треугольник с тем же основанием AB имел такую же площадь, надо, согласно предыдущему п., чтобы его высота равнялась высоте данного. Для этого необходимо, чтобы его вершина была расположена на таком же расстоянии от прямой AB, как и точка C. Таких точек бесчисленное множество и все они расположены на прямой MN, параллельной основанию и проходящей чрез точку C. Конечно, возможно на таком же расстоянии построить еще другую параллельную AB, по другую ее сторону.
Итак, геометрическое место вершин треугольников, равновеликих между собою и имеющих общее основание, есть прямая (или две прямых), параллельная основанию.
Иногда то же свойство выражают в такой форме:
От перенесения вершины треугольника по прямой, параллельной основанию, его площадь не изменится.
158. Упражнения.
1. Превратить данный треугольник ABC в равновеликий ему с тем же основанием AB, но чтобы угол при точке A был данный.
2. Превратить данный треугольник ABC в равновеликий ему с тем же основанием AB, но чтобы сторона, выходящая из точки A, была равна данному отрезку.
3. Превратить ∆ABC в равновеликий ему равнобедренный с тем же основанием AB.
Надо воспользоваться геометрическим местом п. 157 и геометрическим местом вершин равнобедренных треугольников, имеющих основание AB, – этим местом является перпендикуляр к AB чрез его середину.
4. Превратить ∆ABC в равнобедренный ему треугольник с другим основанием AD (чер. 168).
Соединив C с D, построив BE || CD и соединив E с D, получим искомый ∆AED (часть ABE осталась неизменною, а ∆BEC равновелик ∆BED).
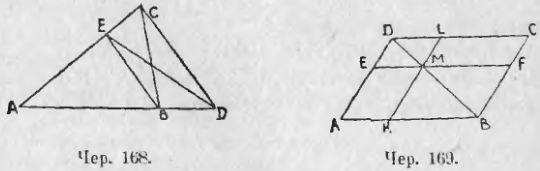
Мы увеличили основание (было AB, стало AD). Можно также уменьшить его.
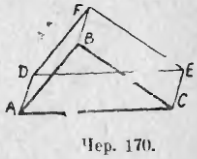
5. На диагонали BD параллелограмма ABCD (чер. 169) взята точка M и чрез нее построены прямые EF и KL, параллельные сторонам параллелограмма. Тогда параллелограммы AKME и MFCL равновелики.
6. На сторонах ∆ABC (чер. 170) построены параллелограммы ACED, CEFB и BFDA (сторона BF, если ее продолжить, пройдет внутри отрезка AC). Параллелограмм ACED равновелик сумме параллелограммов ABFD и BCEF.
7. Превратить данный параллелограмм в равновеликий ему ∆ с тою же высотой.
159. Задача 1. Превратить данный параллелограмм в равновеликий ему с данным основанием.
Пусть дан параллелограмм ABFE (чер. 169) и требуется превратить его в равновеликий ему с основанием, равным отрезку BK. Отложив данное основание BK на основании BA данного параллелограмма, как это сделано на чертеже, построим прямую KML || AE; затем построим прямую BM и продолжим ее до пересечения в точке D с продолжением стороны AE данного параллелограмма. Наконец, построим прямую DC || AB, которая пересекает прямую KML в точке L и продолжение прямой BF в точке C. Тогда параллелограмм KBCL есть искомый.
В самом деле: ∆DML = ∆DME; ∆BDC = ∆BDA; след., площ. BMLC = площ. BMEA; но ∆BMF = ∆BMK; след., площ. BMLC + площ. BMK = площ. BMEA + площ. BMF, или площ. BKLC = площ. BFEA. Совершенно так же решается задача о построении прямоугольника, равновеликого данному и имеющего данное основание.
Задача 2. Превратить 4-угольник в равновеликий ему треугольник.
Пусть требуется 4-угольник ABCD (чер. 171) превратить в равновеликий ему треугольник.
Для этого диагональю BD разобьем площадь четырехугольника на две части и один из треугольников, напр. ∆ABD, превратим в равновеликий ему с тем же основанием BD так, чтобы один из углов 4-угольника, напр. ∠B, выпрямился. Для этого надо вершину A перенести по прямой, параллельной основанию BD, в точку K, где эта параллельная пересекается с продолжением стороны BC. Тогда ∆KBD равновелик ∆ABD и, следовательно, ∆DKC равновелик 4-угольнику ABCD.
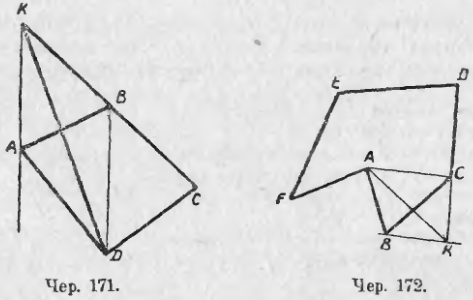
Пусть теперь имеем 6-угольник ABCDEF (чер. 172). Отсечем диагональю AC сначала ∆ABC и превратим его в равновеликий ему ∆AKC с тем же основанием AC, где вершина K есть точка пересечения прямой BK || AC с продолжением стороны DC. Тогда наш 6-угольник превратился в равновеликий ему 5-угольник AKDEF. Повторяя тот же прием еще раз, превратим полученный 5-угольник в равновеликий ему 4-угольник, затем последний — в равновеликий ему треугольник. Таким образом, всякий многоугольник, имеющий площадь, можно превратить в равновеликий ему треугольник.
Теперь процесс сложения и вычитания площадей (п. 152) упрощается: каждый из данных многоугольников превратим в равновеликий ему треугольник, построим новый многоугольник, площадь которого равна сумме или разности площадей полученных треугольников (приложим один треугольник к другому, или наложим один на другой) и этот многоугольник превратим опять в равновеликий ему треугольник.
160. Упражнения.
1. Превратить невыпуклый 4-угольник (имеющий площадь) в равновеликий ему треугольник.
2. Построить треугольник, равновеликий сумме данного треугольника и невыпуклого 8-угольника (чер. 173).
Построить также треугольник, равновеликий их разности.
3. Построить ∆, площадь которого была бы в 2, 3... раза больше площади данного ∆, а основание осталось бы то же.
4. В треугольнике ABC проведена средняя линия MN, где M и N суть середины сторон AB и BC. Тогда площадь ∆MBN в 4 раза меньше площади ∆ABC.
5. Стороны BA и BC треугольника ABC продолжены и увеличены в 2 раза каждая. От соединения концов продолжений получится новый треугольник, площадь которого в 4 раза больше площади данного.
6. Стороны BA и BC треугольника ABC (чер. 174) продолжены так, что BK = 3BA и затем построено KL || AC. Площадь ∆KBL в 9 раз больше площади ∆ABC.
Построим еще MN, где M и N середины отрезков AK и CL, APR и CPQ, где P середина отрезка MN, и, наконец, QM и RN. Тогда MQ || AR || BL и NR || CQ || BK.
Легко теперь увидать, что 1) сторона BL в 3 раза больше стороны BC, 2) сторона KL в 3 раза больше стороны AC и 3) площадь ∆KBL в 9 раз больше площади ∆ABC. Итак, если стороны треугольника увеличить в 3 раза, то площадь его увеличится в 9 раз.
7. Во сколько раз увеличится площадь треугольника, если стороны его увеличить в 4 раза каждую? (Как выполнить построение, необходимое для увеличения каждой стороны в 4 раза?)
161. Выполним следующее построение: 1) Из концов гипотенузы AC (чер. 175) прямоугольного треугольника ABC (∠B = d) построим AE ⊥ AC и CD ⊥ AC, отложим AE = CD = AC и соединим точки D и E, – получим квадрат AEDC, стороны которого = AC (AEDC есть квадрат, построенный на гипотенузе). 2) Продолжим AB по направлению BG (BG ⊥ BC), построим CF ⊥ BC и чрез точку D построим прямую GF, перпендикулярную к BG и к CF (ведь CF || BG). Тогда получим квадрат BCFG, сторона которого = катету BC прямоугольного ∆ABC; в самом деле, ∆CDF = ∆ABC, так как CD = AC (по первому построению), ∠DCF = ∠BCA, потому что оба эти угла дополняются углом BCD до прямого, а этого достаточно для равенства прямоугольных треугольников (углы при B и F прямые), следов., CF = BC = BG = GF (CBGF есть квадрат, построенный на катете BC). 3) Построим BK — продолжение BC, AL ⊥ AB (AL || BK) и чрез точку E построим прямую EL, перпендикулярную к BK и к AL. Тогда получится квадрат ABKL, сторона которого равна катету AB прямоугольного ∆ABC. Доказательство, такое же, как и в предыдущем построении, вытекает из равенства треугольников ALE и ABD; ABKL есть квадрат, построенный на катете AB. 4) Продолжим FG и LK до пересечения в точке M.
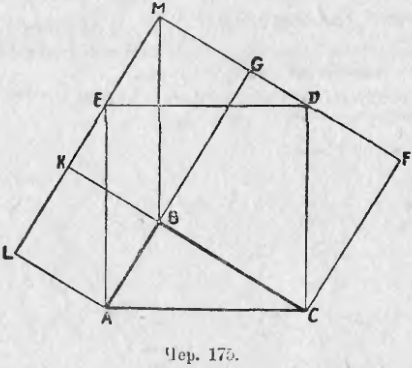
В предыдущем мы нашли, что ∆CDF = ∆ABC и ∆AEL = ∆ABC. Мы можем еще найти треугольники, равные ∆ABC. Прежде всего это ясно для ∆EMD, гипотенуза которого ED равна гипотенузе AC и ∠MED = ∠BAC, как углы с параллельными сторонами. Затем, построив отрезок MB, получим два равных треугольника ∆BMG = ∆BMK (так как MB есть диагональ прямоугольника BKMG). Легко увидать, что KB = AB (стороны квадрата), KM = BG (противоположные стороны прямоугольника) = BC (стороны квадрата). Поэтому ∆BKM = ∆ABC (так как катеты их равны), а следовательно и ∆MGB = ∆ABC.
Итак, имеем:
∆ABC = ∆CFD = ∆AEL = ∆EMD = ∆BKM = ∆MGB.
Рассмотрим площадь ACFMLA. Если от этой площади отрезать куски, занимаемые треугольниками AEL, EMD и CDF, то останется площадь, занимаемая квадратом AEDC, то есть
площ. AEDC = площ. ACFMLA – 3 площ. ∆ABC.
Но такие же три части мы можем отрезать от площади пятиугольника ACFML иным способом, отрезав площади треугольников BMK, BGM и ABC, – эти три треугольника равны, как мы уже нашли, прежним. Отняв от площади, занимаемой пятиугольником ACFML, площади треугольников BMK, MBG (или сразу отнять площадь прямоугольника BKMG) и ABC, получим площади, занимаемые квадратами ALKB и BGFC, т. е. площ. ALKB + площ. BGFC = площ. ACFMLA – 3 пл. ∆ABC.
Так как в обоих случаях мы отнимали поровну (утроенную площадь ∆ABC), то остатки должны быть равны, т. е.
площ. AEDC = площ. ALKB + площ. BGFC,
или в словесной форме:
Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах.
Это свойство известно под именем теоремы Пифагора.
Можно и иными способами (их много) выяснить то же свойство. Вот еще два из них:
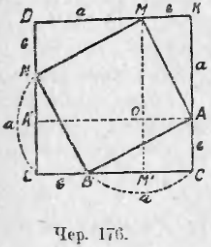
1) Пусть имеем прямоугольный ∆ABC (чер. 176). Обозначим его катеты каждый одною буквою: BC = a и AC = b. Отложим на продолжениях катетов отрезки BL = b и AK = a и построим квадрат CKDL, сторона которого = a + b. Далее построим точки M и N так, чтобы KM = b, MD = a, DN = b и NL = a и соединим A с M, M с N и N с B; тогда получим квадрат AMNB, площадь которого получается, если от площади квадрата CKDL отнять площади 4 равных треугольников ABC, AMK и т. д. Построив затем прямые AA' || CL и MM' || KC, получим два квадрата: OMDA', сторона которого = a и OACM', сторона которого = b; сумма площадей этих квадратов получается, если от площади квадрата CKDL отнять площади 2 прямоугольников OAKM и OM'LA', каждый из которых имеет стороны a и b и площадь каждого равна удвоенной площади ∆ABC (ясно видно, например, что площ. OAKM = 2 площ. ∆AMK, но AMK = ∆ABC).
Отсюда вытекает справедливость теоремы Пифагора.
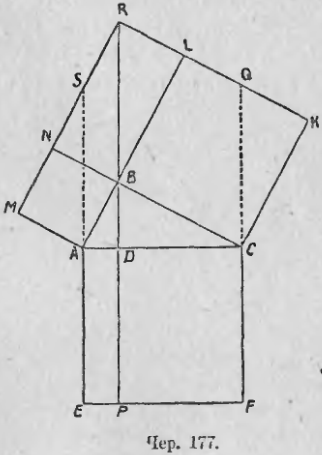
2) Пусть имеем прямоугольный ∆ABC (чер. 177). Построим квадраты AF, AN и BK на его гипотенузе и катетах и продолжим стороны LK и MN до пересечения в точке R. Затем построим прямую BR и продолжим стороны AE и CF до пересечения в S и в Q с прямыми MR и RK. Тогда ∆BLR = ∆ABC, так как у них равные катеты BL = BC, LR = BN = AB; следовательно, BR = AC = AE = CF. Кроме того, ∠RBL = ∠ACB, но ∠BCA = ∠QCK, так как каждый из них дополняется углом BCQ до прямого. Поэтому ∠RBL= ∠QCK и, следовательно, RB || QC || SA и, след., RB = QC = SA. Продолжим RB до пересечения со сторонами квадрата AF в точках D и P; тогда BP ⊥ AC и BP ⊥ EF (ибо RP || SE). Параллелограмм ASRB равновелик прямоугольнику EADP (у них равные основания PD = BR и одинаковые высоты), по тот же параллелограмм ASRB равновелик квадрату AMNB. Также найдем, что прямоугольник PDCF равновелик квадрату CBLK, а, следовательно, квадрат ACFE равновелик сумме квадратов AMNB и BLKC.
162. Упражнения.
1. Вершины L и F квадратов, построенных на катетах (чер. 175), расположены на одной прямой с точкой B, вершиной прямого угла треугольника.
2. Построить квадрат равновеликий сумме данных двух квадратов.
3. Построить квадрат равновеликий разности двух данных квадратов.
4. Построим на чер. 177 прямые BE и MC, которые пересекутся пусть в точке X; тогда точки E, A, X и C лежат на одном круге, диаметр которого есть EC. (Выясняется это так: ∆ABE = AMC, откуда ∠AEX = ∠ACX). Отсюда вытекает, что CM ⊥ BE. Далее легко найти, что AR || BE и, следовательно, CM ⊥ AR.
Пользуясь этим, показать:
5. Прямые CM и AK пересекаются на BD (BD ⊥ AC).
163. Превратить трапецию в равновеликий треугольник.
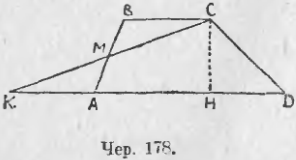
Пусть имеем трапецию ABCD (чер. 178). Найдем середину M одной из ее непараллельных сторон, построим прямую CM и найдем ее точку пересечения K с прямой DA. Тогда ∆AMK = ∆MBC и, следовательно, трапеция ABCD равновелика ∆KCD, у которого та же высота (CH), а основание KD = KA + AD = BC + AD, то есть трапеция равновелика треугольнику, имеющему такую же высоту, а основание которого равно сумме параллельных сторон трапеции.
