164. Если нам дано уравнение
y = 3x (1)
мы можем найти бесчисленное множество решений этого уравнения: можно принять x равным любому числу (например, 0; 1; 2; 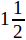 и т. д.); тогда найдем соотв. число для y (0; 3; 6;
и т. д.); тогда найдем соотв. число для y (0; 3; 6; 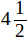 и т. д.).
и т. д.).
Данное уравнение можно еще написать в виде
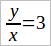 (2)
(2)
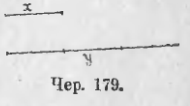
Пусть теперь требуется построить два отрезка таких, чтобы они удовлетворяли уравнению (1). Эта задача также легко решается: построим (чер. 179) произвольный отрезок x и затем на какой-либо прямой отложим от какой-либо ее точки этот отрезок 3 раза, – получим искомый отрезок y. Таких пар отрезков, удовлетворяющих уравнению (1), можно найти бесчисленное множество. Принято и в том случае, когда x y в уравнении (1) означают не числа, а отрезки, писать это уравнение не только в виде уравнения (1), но и в форме уравнения (2), хотя мы и не умеем делить отрезок y на отрезок x. Можно смотреть на уравнение (2) с той точки зрения, что здесь дается новая форма для выражения числа 3: число 3 здесь представлено в виде символа 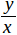 , где y и x отрезки. Этот символ
, где y и x отрезки. Этот символ 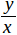 называется отношением отрезка y к отрезку x.
называется отношением отрезка y к отрезку x.

Подобно этому, можно также решить отрезками уравнение 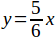 (см. чер. 180), для чего надо лишь умение делить любой отрезок на сколько угодно равных частей. Так же точно, согласно предыдущему условию, мы можем, понимая под y и x отрезки, написать наше уравнение в виде
(см. чер. 180), для чего надо лишь умение делить любой отрезок на сколько угодно равных частей. Так же точно, согласно предыдущему условию, мы можем, понимая под y и x отрезки, написать наше уравнение в виде 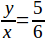 , которое прочтем: «отношение отрезка y к отрезку x равно числу
, которое прочтем: «отношение отрезка y к отрезку x равно числу 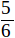 . На последнее уравнение можно также смотреть, как на новую форму выражения числа
. На последнее уравнение можно также смотреть, как на новую форму выражения числа 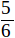 . Из этих примеров можно прийти к общему заключению:
. Из этих примеров можно прийти к общему заключению:
всякое целое или дробное число можно представить в форме отношения двух отрезков.
165. Возникает мысль о задаче, обратной тем, какие решались в предыдущем п., т. е.: даны два отрезка A и B (чер. 181); требуется для них составить уравнение вида A = k · B или A/B = k, где k — какое-либо число.
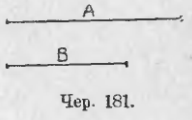
Если действительно удастся составить такое уравнение, если, напр., получим A = 37B или получим 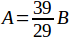 , то мы видим, что решение этой задачи должно основаться на существовании такого третьего отрезка, который укладывается на каждом из данных по целому числу раз; в примере A = 37B таким отрезком является сам B: он укладывается 37 раз на отрезке A и 1 раз на самом себе; во втором примере (
, то мы видим, что решение этой задачи должно основаться на существовании такого третьего отрезка, который укладывается на каждом из данных по целому числу раз; в примере A = 37B таким отрезком является сам B: он укладывается 37 раз на отрезке A и 1 раз на самом себе; во втором примере (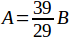 ) таким отрезком является отрезок, равный
) таким отрезком является отрезок, равный 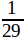 части отрезка B: он укладывается 39 раз на отрезке A и 29 раз на отрезке B.
части отрезка B: он укладывается 39 раз на отрезке A и 29 раз на отрезке B.
Принято называть
общею мерою двух отрезков такой третий отрезок, который укладывается по целому числу раз на каждом из данных отрезков.
В первом из предыдущих примеров (A = 37B) общею мерою отрезков A и B служит сам отрезок B: он укладывается 37 раз на A и один раз на B.
Во втором случае (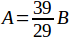 ) общей мерою отрезков A и B служит 29-я доля отрезка B: она укладывается 39 раз на A и 29 раз на B.
) общей мерою отрезков A и B служит 29-я доля отрезка B: она укладывается 39 раз на A и 29 раз на B.
Итак, для решения нашей обратной задачи необходима общая мера двух данных отрезков. Вот пример, на котором выясняется, как можно в некоторых случаях найти общую меру двух отрезков.
Пусть имеем отрезок AB и отрезок CD (чер. 182). Попытаемся найти общую меру отрезков AB и CD.
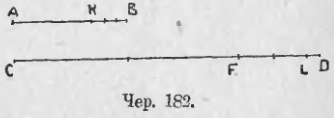
Попытаем сначала, не уложится ли меньший из них, в данном случае отрезок AB, на отрезке CD целое число раз. Если AB уложится на CD целое число раз, то AB и есть общая мера между AB и CD (на AB укладывается 1 раз и на CD укладывается, например, 3 раза). Допустим, что AB на CD укладывается 2 раза с остатком FD. Тогда попытаем, не уложится ли этот остаток FD на отрезке AB целое число раз: если бы уложился целое число раз на AB, то и уложился бы целое число раз и на CF и на CD, т. е. тогда отрезок FD был бы общею мерою. Допустим (как на чертеже), что FD на AB укладывается 1 раз с остатком KB. Тогда, исходя из тех же соображений, пробуем, не уложится ли KB на FD без остатка; допустим, что KB на FD укладывается 2 раза с остатком LD. Затем пробуем, не уложится ли LD на KB без остатка и допустим, что, наконец, достигли этого, т. е. пусть LD укладывается на KB 3 раза без остатка. (Делая это допущение, мы тем самым признаем возможность случая, что никогда не достигнем того, чтобы полученный остаток в предыдущем укладывался целое число раз без нового остатка.) Тогда LD и является общею мерою. Остается сосчитать, сколько раз эта общая мера укладывается на отрезках AB и CD. Для этого запишем те наложения, которые мы выполняли.
CD = 2AB + FD | CD = 27LD
AB = FD + KB | AB = 10LD
FD = 2KB + LD | FD = 7LD
KB = 3LD |
Второй столбец этой записи составляется по направлению снизу вверх: FD = 2KB + LD = 6LD + LD = 7LD; AB = FD + KB = 7LD + 3LD = и т. д.
Теперь мы видим, что общею мерою наших отрезков является отрезок LD, который есть 1/10 доля отрезка AB, так как AB = 10LD, т. е.
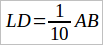
Но мы получили, что CD = 27LD; следовательно,

Второе из этих уравнений читают: отношение отрезка CD к отрезку AB равно числу 27/10, а первое можно понимать так: отрезок CD измерили отрезком AB (принимая за единицу отрезок AB) и получили число 27/10, подобно тому, как запись:
«Высота дерева равна 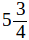 аршина» понимают в том смысле, что высота дерева (отрезок) измерена аршином и получилось число
аршина» понимают в том смысле, что высота дерева (отрезок) измерена аршином и получилось число 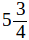 .
.
Если бы, наоборот, нам потребовалось найти AB/CD (отношение AB к CD) или измерить отрезок AB, принимая за единицу CD, то, конечно, общая мера осталась бы та же самая, т. е. LD, но тогда отрезок LD был бы 1/27 долею единицы CD, т. е.

Нахождение общей меры выполняется в таком порядке: укладываем меньший отрезок на большем, полученный остаток на меньшем, новый остаток на предыдущем и т. д., пока остатка не получится; последний остаток и является общею мерою двух данных отрезков.
Следует заметить, что найденная таким образом общая мера является наибольшею: всякая часть ее также будет общею мерою; например, если найденная общая мера укладывается 10 раз на AB и 27 раз на CD, то ее третья доля укладывается 30 раз на AB и 81 раз на CD.
166. Изложим теперь в общем виде ход мысли при решении задачи «найти отношение двух данных отрезков», допуская, что они имеют общую меру.
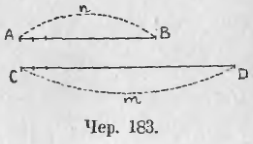
Пусть требуется найти CD/AB (чер. 183) или, что то же самое, измерить отрезок CD, принимая за единицу отрезок AB. Тогда находим согласно предыдущему общую меру отрезков CD и AB (согласно допущению это возможно) и рассуждаем теперь в общем виде: положим, что общая мера на отрезке AB укладывается n раз и на отрезке CD — m раз. Тогда общая мера равна 1/n доли единицы AB и таких долей в CD уложилось m. Следовательно,

Последнее уравнение можно истолковать так: дробь m/n выражена в новой форме, в виде отношения отрезков CD и AB.
Возникает вопрос, всегда ли возможно найти общую меру двух данных отрезков? Быть может, сколько бы мы ни продолжали процесс ее нахождения, никогда не удастся дойти до того, чтобы последний остаток уложился на предыдущем целое число раз? Практика не может дать ответа на этот вопрос, так как с одной стороны, какой бы хороший циркуль мы ни употребляли для отложения отрезков, всегда при этом делаются ошибки, а с другой стороны, приходится иметь дело со столь мелкими отрезками, что невозможно решить вопрос, откладывается ли полученный отрезок на другом без остатка.
В следующем п. мы рассуждением убедимся, что мы можем построить такие отрезки, которые не имеют общей меры.
Два отрезка, имеющие общую меру, называются соизмеримыми, а неимеющие общей меры, называются несоизмеримыми.
167. Построим прямоугольный равнобедренный треугольник ABC (чер. 184); это построение легко выполняется: строим прямой угол B и на его сторонах откладываем произвольные, но равные отрезки BA = BC.
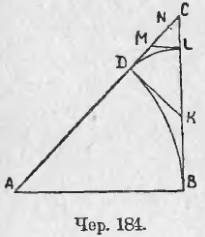
Станем искать общую меру между его гипотенузою AC и одним из катетов. Для этого надо сначала отложить, сколько возможно раз, катет AB на гипотенузе AC. Возникает вопрос, который надо решить рассуждением: сколько раз можно AB уложить на AC. Несомненно, можно один раз, ибо гипотенуза больше катета (п. 86), но двух раз уложить нельзя, так как мы знаем (п. 90), что AC < AB + BC или, в виду равенства AB = BC, AC < 2AB. Следовательно, катет AB укладывается на гипотенузе AC один раз с остатком. Чтобы найти остаток, построим дугу, принимая A за центр, радиусом = AB; тогда, называя чрез D точку пересечения дуги с гипотенузою AC, имеем AD = AB и, следовательно, остатком является отрезок DC. Теперь следует отрезок DC укладывать на катете AB, или, что то же самое, на катете BC (ведь BC = AB). Для этого из точки D строим DK ⊥ AD. Тогда 1) ∆DCK прямоугольный равнобедренный, так как ∠C является углом равнобедренного прямоугольного треугольника ABC, равен ½d, следовательно, и ∠K = ½d (так как сумма ∠C + ∠K должна равняться d). Следовательно, ∠C = ∠K, откуда KD = DC.
2) DK = KB, так как это суть отрезки касательных, проведенных к кругу через точку K (KB ⊥ AB, следовательно, KB есть касательная; так же и KD), ограниченные этою точкою K и точками касания (п. 139). Итак, имеем BK = KD = DC, т. е. на катете BC уложили один раз отрезок DC, после чего остается остаток KC, который служит гипотенузою прямоугольного равнобедренного треугольника KDC. Мы уже теперь, на основании исследования прямоугольного равнобедренного треугольника ABC, можем утверждать: 1) что катет DC этого треугольника уложится на KC один раз с остатком (следовательно, DC укладывается на BC два раза с остатком), 2) что после этого мы придем опять к тому же: этот остаток (CL) должно укладывать на катете DC прямоугольного равнобедренного треугольника KDC, и он, как мы уже знаем, уложится на DC два раза с остатком (CN), который в свою очередь уложится на CL два раза с остатком и т. д. Из этого мы видим, что наш процесс нахождения общей меры никогда не должен кончиться: всякий раз, отложив последний остаток один раз на предыдущем, мы придем опять к прямоугольному равнобедренному треугольнику, катет которого надо откладывать на гипотенузе, а мы знаем, что он уложится на гипотенузе еще один раз с остатком, - следовательно, всякий раз последний остаток укладывается в предыдущем два раза с остатком. Итак, общей меры нет, т. е.
Гипотенуза и катет равнобедренного прямоугольного треугольника несоизмеримы.
168. Целые и дробные числа вместе называются рациональными числами. Если мы хотим считать, что отношение двух отрезков y и x, т. е. символ y/x всегда равен числу, то рациональных чисел недостаточно, и математика расширяет понятие о числе 1) так, чтобы всегда можно было считать, что отношение двух отрезков равно числу: если отрезки соизмеримы, то отношение их равно какому-либо рациональному числу; если отрезки несоизмеримы, то условимся, что их отношение выражает собою какое-то новое число, которое назовем иррациональным.
1) Расширение понятия о числе проводится во всем курсе математики: первоначально мы имеем дело лишь с целыми числами; желание, чтобы действие деление всегда оказалось бы выполнимым, заставляет обобщать понятие о числе, – и мы вводим в семью чисел дробные числа; желание, чтобы вычитание оказалось всегда возможным, заставляет еще в семью чисел ввести отрицательные числа. Далее вводится еще иррациональные и мнимые числа. Каждое обобщение понятия о числе должно быть сделано так: 1) надо, чтобы все члены расширенной области чисел оказались равноправными; 2) надо, чтобы о каждой паре чисел можно было бы установить, равны ли они между собою, или одно из них больше другого (или меньше), причем должны иметь место аксиомы для понятий «равно», «больше» и «меньше» [a) если A = B, то и B = A; b) если A = B и B = C, то A = C; с) если A = B и B > C, то A > C]; 3) чтобы над любыми числами расширенной области можно было выполнять все действия, причем по возможности сохранились бы все законы действий.
Таким образом, на символ y/x, где y и x суть отрезки, мы всегда можем смотреть, как на число. Если это число мы назовем через k, то имеем
y/x = k или y = kx.
Мы сперва остановимся на первом из этих уравнений. Его можно понимать так:
Если даны два отрезка (напр., y и x), то всегда существует отношение этих отрезков, прямое и обратное (т. е. y/x и x/y), причем каждое отношение двух отрезков служит новою формою для выражения чисел: иногда оно выражает знакомы нам из курса арифметики рациональные числа, а иногда, если отрезки (y и x) несоизмеримы, выражает новое, иррациональное, число.
Все числа, и рациональные и иррациональные, обладают признаком равноправности: они выражаются в одной и той же форме, – в форме отношения двух отрезков.
169. О всяких двух данных рациональных числах мы можем узнать, равны ли эти числа, или одно из них больше другого. Теперь надо расширить это умение и научиться узнавать о всяких двух числах, будут ли они рациональны или иррациональны или одно из них рационально, а другое иррационально, равны ли эти числа или одно из них больше другого.
Так как каждое из тех чисел, с которыми мы имеем теперь дело, выражается отношением двух отрезков, то мы должны научиться применять понятия «больше», «меньше», «равно» к отношениям отрезков, подобно тому, как мы это умеем делать для рациональных чисел, для отрезков, для углов, для площадей, ограниченных прямыми линиями.
Для этой цели сперва рассмотрим ряд отношений с одинаковыми последующими членами, например:
y/x; y1/x; y2/x; …
Мы можем признать, что одно из этого ряда отношений равно, больше или меньше другого, смотря по тому, будет ли предыдущий член первого отношения равен, больше или меньше предыдущего члена второго, т. е
y1/x = y2/x, если y1 = y2
y1/x > y2/x, если y1 > y2
y1/x < y2/x, если y1 < y2
Ясно, что мы не впадаем здесь в противоречие с тем, как мы прилагаем понятия «равно», «больше» и «меньше» к рациональным числам: если отрезки y1 и y2 соизмеримы с x, то отношения y1/x и y2/x выражают рациональные числа, и ясно, что для них предыдущие условия справедливы.
170. Прежде чем перейти к случаю, когда у рассматриваемых отношений последующие члены различны, мы должны остановиться на следующем факте.
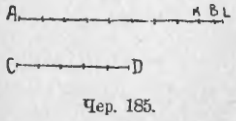
Если имеем два несоизмеримых отрезка AB и CD (чер. 185), то можно построить два новых отрезка, удовлетворяющих условиям:
1) Оба они соизмеримы, например, с отрезком CD и один из них меньше отрезка AB, а другой больше.
2) Разность между ними равна любой доле, сколь угодно малой, отрезка CD.
Выберем, например, пятую долю отрезка CD. Тогда, чтобы построить два указанных отрезка, поступаем следующим образом (Здесь мы пользуемся едва уловимою, благодаря своей очевидности, аксиомою Архимеда: если отрезок a больше отрезка b, то всегда можно найти такое целое число n, чтобы было nb < a, но (n + 1)b > a): разделим отрезок CD на 5 равных частей и станем эту часть откладывать на отрезке AB, – пусть, например, она уложилась 8 раз с остатком KB, который, следовательно, < 1/5 CD; тогда получим отрезок AK, удовлетворяющий уравнению
AK = 8/5 CD (1)
Отложив от K еще 1/5 долю CD, получим отрезок AL, о котором напишем
AL = 9/5 CD (2)
Два полученных отрезка AK и AL и суть искомые:
1) Один из них AK < AB и другой AL > AB; оба они соизмеримы с CD, 2) разность между ними = 1/5 CD, т. е.
AL – AK = KL = 1/5 CD.
Отсюда мы получаем на основании п. 169: так как AB > AK, то AB/CD > AK/CD, но AK/CD = 8/5 [из равенства (1)], – следовательно, AB/CD > 8/5; так как AB < AL, то AB/CK < AL/CD, но AL/CD = 9/5 [из равенства (2)], – следовательно, AB/CD < 9/5.
Эти неравенства можно соединить вместе:
8/5 < AB/CD < 9/5,
т. е. нам удалось установить, что отношение наших двух несоизмеримых отрезков AB и CD (или равное ему иррациональное число) заключается между числами 8/5 и 9/5. Эти числа разнятся между собою на 1/5 (9/5 – 8/5 = 1/5), а, следовательно, отношение AB/CD разнится от одного из них меньше, чем на 1/5. Поэтому говорят, что узнали отношение AB/CD с точностью до 1/5.
Если бы мы разделили сначала отрезок CD на 10 равных частей, то также нашли бы два отрезка, соизмеримых с CD, между которыми заключается отрезок AB, причем разность между ними равнялась бы 1/10 CD. Тогда получили бы, например,
17/10 < AB/CD < 18/10.
Это неравенство можно было бы толковать так: нам удалось узнать отношение AB/CD с точностью до 1/10. Так же можно было бы узнать это отношение с точностью до 1/100, до 1/1000 и т. д.
Иногда даже пишут AB/CD = (прибл.) 17/10 или = (прибл.) 18/10.
171. Мы таким образом здесь научились находить рациональные числа, меньшие и большие отношении двух несоизмеримых отрезков. Легко теперь расширить это умение, а именно:
О всяком рациональном числе, целом или дробном, мы можем установить, равно ли оно отношению двух данных отрезков, или больше, или меньше его.
Пусть даны два отрезка AB и CD (чер. 185) и дано число p/q (например, 8/15). Мы можем разделить отрезок CD на q (на 15) равных частей и взять таких частей p (8); тогда получим отрезок = p/q CD (= 8/15 CD). Если этот отрезок окажется равным отрезку AB, то (п. 169) p/q = AB/CD (8/15 = AB/CD); если этот отрезок окажется меньше AB, то p/q < AB/CD (8/15 < AB/CD); если, наконец, этот отрезок окажется больше AB, то p/q > AB/CD (8/15 > AB/CD).
Добавление. Из предыдущего мы видим свойства, которыми должны обладать новые числа, введенные нами для выражения отношения двух несоизмеримых отрезков: 1) мы можем найти такое целое или дробное число, чтобы оно отличалось от нашего нового числа, выражающего отношение двух данных несоизмеримых отрезков, меньше чем на любую долю единицы (можно вычислять это новое число с любой точностью), но оно не может равняться никакому целому или дробному числу; 2) о всяком целом или дробном числе мы можем установить, больше ли оно или меньше нового числа, выражающего отношение двух данных несоизмеримых отрезков.
Можно, обобщая понятие о числе, не опираться на отрезки, но ввести иррациональные числа, как символы, которые указывали бы возможность как-либо обосновать два предыдущих свойства. Частным случаем иррациональных чисел являются те числа, которые вводятся в курс алгебры для того, чтобы считать символы √2, ∛4, √5 и т. п. за числа. Например, для √2 мы имеем, что он не может равняться ни целому, ни дробному числу, но
1,4 < √2 < 1,5
1,41 < √2 < 1,42 и т. д.
Эти равенства указывают возможность вычислить √2 с любою точностью. Кроме того, для всякого рационального числа можно установить, считать ли его больше или меньше √2, например, возьмем число 1,41423 и возведем его в квадрат – получим 2,0004465129, т. е. больше 2; поэтому 1,41423 > √2; возьмем еще число 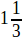 и возведем его в квадрат, – получим
и возведем его в квадрат, – получим 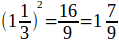 , т. е. меньше 2; поэтому
, т. е. меньше 2; поэтому 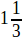 < √2.
< √2.
172. Можно приближенно вычислять отношение двух несоизмеримых отрезков и без уменья делить отрезок на равные части.
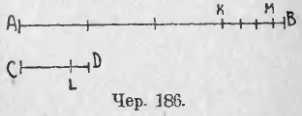
Пусть имеем 2 несоизмеримых отрезка AB и CD (чер. 186). Отложим меньший из них CD на AB, – пусть он отложится 3 раза с остатком KB; затем отложим KB на отрезке CD — пусть он уложится 1 раз с остатком LD; затем откладываем отрезок LD на KB, – пусть он уложится 3 раза с остатком MB. Этот процесс откладывания нового отрезка на предыдущем здесь никогда не кончится, так как отрезки AB и CD предполагаются несоизмеримыми. Но мы можем для приближенного вычисления отношения AB к CD принять, применяясь к чертежу 186, что остаток MB очень близок к отрезку LD и тогда счесть приблизительно, что LD укладывается на KB ровно 4 раза. Тогда имеем:
AB = 3CD + KB; CD = KB + LD; KB = (прибл.) 4LD.
Откуда
CD = (прибл.) 5LD и AB = (прибл.) 19LD.
Отсюда мы можем заключить, что
AB = (прибл.) 19/5 CD или AB/CD = (прибл.) 19/5.
Для того, чтобы дать здесь ответ на существенный вопрос приближенного вычисления, каков здесь предел ошибки, надо знать теорию непрерывных дробей. Заметим лишь, что этот ответ ждать можно.
Возможно было бы, если остаток MB оказался мал, вовсе пренебречь им и принять, что KB = (прибл.) 3LD; тогда получили бы другое приближенное значение для AB/CD.
Если бы мы продолжили дальше процесс отложения: отложили MB на LD (например, 1 раз с остатком), новый остаток на MB и т. д., то, прервав где-либо этот процесс и приняв, что один из остатков равен приблизительно последующему остатку, повторенному целое число раз, мы получили бы другое приближенное значение для AB/CD, более точное.
Теория непрерывных дробей могла бы дать указание, сколь далеко надо продолжить этот процесс, чтобы получить приближенное значение для нашего отношения с точностью, например, до 1/100.
173. Перейдем теперь к рассмотрению вопроса, как применять понятия «больше», «меньше» и «равно» к двум отношениям с различными последующими членами. Иногда удается воспользоваться арифметическими соображениями. Например, если мы получили AB/CD = 4/5 и A'B'/C'D' = 4/5 (где AB, CD, A'B' и C'D' суть отрезки), то ясно, что AB/CD = A'B'/C'D'; также, если удалось узнать, что AB/CD = 2/3, а A'B'/C'D' = 4/5, то, принимая во внимание, что 4/5 > 2/3 (4/5 = 12/15, 2/3 = 10/15), мы имеем AB/CD < A'B'/C'D' или A'B'/C'D' > AB/CD.
Но случай, когда возможно воспользоваться арифметикою, редки, и нам необходимо разобрать вопрос о равенстве или неравенстве двух отношений в предположении, что мы не знаем, какому именно числу равно каждое из них (а если AB и CD несоизмеримы, то символ AB/CD мы не всегда даже в состоянии заменить другим символом, выражающим то же число в арифметической форме).
Для выяснения вопроса обратимся сначала к арифметике. Пусть даны два числа 2/9 и 5/24; найти число большее одного из них и меньшее другого.
Для этого приведем наши дроби к общему знаменателю:
2/9 = 16/72 и 5/24 = 15/72.
Мы видим, что требуемое число нельзя найти в виде дроби со знаменателем 72. Поэтому, обращаясь к более мелким долям, получим: 2/9 = 32/144 и 5/24 = 30/144. Отсюда находим искомое число 31/144.
Далее, так как
2/9 = 48/216 и 5/24 = 45/216
то вот еще искомые числа: 46/216 и 47/216.
Раздробляя 2/9 и 5/24 в еще более мелкие доли, найдем, что искомых чисел бесконечно много. Возможность нахождения таких чисел имеет причиною, что 2/9 и 5/24 не равны (5/24 < 2/9). Если же нам даны два равных числа, хотя бы и в различной форме, напр., 5/8 и 10/16, то найти указанные числа невозможно.
Теперь нам числа даются в особой форме: в виде отношений отрезков. Мы не умеем изменить эту форму так, чтобы отношение двух отрезков оставалось равным самому себе, но чтобы последующий член сделался одинаковым с последующим членом другого отношения (так мы в арифметике поступаем с дробями с целью узнать, какая из них больше), но зато мы умеем (п. 171) всякое рациональное число сравнивать с отношением двух данных отрезков. Поэтому мы можем те заключения, какие вывели из решения предыдущей арифметической задачи, применить к сравнению двух отношений отрезков, независимо от того, соизмеримы ли или нет эти отрезки:
Два отношения (двух пар отрезков) равны между собою, если нельзя найти рационального числа так, чтобы оно было больше одного из этих отношений и меньше другого.
Если же, наоборот, удается найти такое рациональное число p, чтобы p было больше AB/CD, но чтобы p < A'B'/C'D', то наши отношения AB/CD и A'B'/C'D' не равны, а именно A'B'/C'D' > AB/CD.
174. Мы можем простыми геометрическими построениями получить 2 пары отрезков, отношения которых равны между собою. Построим ∠A (чер. 187) и на одной его стороне отложим равные отрезки: AB = BC = CD, затем построим BB' || CC' || DD'; тогда, согласно п. 111, получим AB' = B'C' = C'D'. Теперь нетрудно составить несколько пар равных отношении: AB/BD = A'B'/B'D' (каждое отношение = ½; общая мера отрезков AB и BD есть AB, а отрезков AB' и B'D' есть AB') AC/AD = AC'/AD' (каждое отношение = 2/3; общая мера для AC и AD есть также AB, а для AC' и AD' — также AB') и т. п.
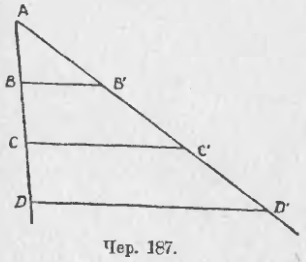
175. Можно обобщить предыдущий пример: построим ∠A (чер. 188) и пересечем его произвольно, не откладывая каких-либо равных отрезков, параллельными BD, CE, MN. Не окажется ли, что и здесь отношение каких-либо двух отрезков на одной стороне угла равным отношению соответствующих двух отрезков на другой стороне? Рассмотрим, напр., отношения BC/AB и DE/AD.
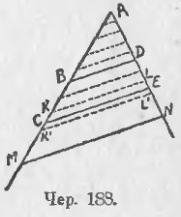
Выберем самое большое число со знаменателем n, где n любое целое число, так, чтобы оно было меньше отношения BC/AB. Для этого разделим отрезок AB на n равных частей и станем эти части откладывать на отрезке BC; допустим, что их уложится m с остатком KC. Тогда имеем: BK < BC и, следовательно, BK/AB < BC/AB, но BK/AB = m/n; следовательно, m/n < BC/AB.
Построив ряд прямых параллельных BD и CE чрез концы отложенных n-ых долей AB, увидим, что этими прямыми отрезок AD разделится на n равных частей (п. 111) и таких частей на отрезке DE уложится m с остатком LE. Тогда DL < DE, и следовательно, DL/AD < DE/AD, но DL/AD = m/n. Отсюда заключаем, что число m/n меньше также и отношения DE к AD, т. е.
m/n < DE/AD.
Отсюда мы видим, что всякое число, меньшее одного из наших отношений, должно быть меньше другого. Мы говорим «всякое число» потому, что число n мы можем выбрать каким угодно, а числитель дроби m/n мы брали так, чтобы получилась наибольшая дробь со знаменателем n, меньшая отношения BC/AB.
[ Точно так же можно увидать, что всякое число, большее первого отношения, должно быть больше и второго, для этого надо рассмотреть наименьшее число со знаменателем n, большее отношения BC/AB, а для этого надо от точки K отложить одну n-ую долю AB, до точки K'. Тогда BK' > BC и, следовательно, BK'/AB > BC/AB', но BK'/AB = (m+1)/n, следовательно,
(m + 1)/n > BC/AB.
Построив чрез K' прямую K'L' || CE, найдем на другой стороне угла точку L' так, что DL' > DE и, следов., DL'/AD > DE/AD, но DL'/AD = (m + 1)/n. Поэтому
(m + 1)/n > DE/AD.
Итак, даже наименьшая из дробей со знаменателем n, которая больше отношения BC/AB, оказывается больше, чем и отношение DE/AD. ]
Отсюда общее заключение: нельзя найти такого числа, которое было бы меньше одного из отношений BC/AB и DE/AD и в то же время больше другого из них; следовательно, признак равенства двух отношений (п. 173) оправдывается, т. е.
BC/AB = DE/AD.
Если оказалось бы, что n-ая доля AB уложилась на BC m раз без остатка, то тогда BC/AB = m/n и при помощи параллельных увидим, что и DE/AD = m/n, т. е. и здесь оправдалось бы вышенаписанное равенство.
Мы могли бы взять также на первой стороне отрезок AC и на другой — ему соответствующий отрезок AE.
Тогда, рассматривая отношения AC/AB и AE/AD, мы увидали бы, что наибольшее число со знаменателем n, которое меньше отношения AC/AB, есть (m + n)/n и оно, как легко видеть, меньше также и отношения AE/AD. [ Точно так же наименьшее число (m + n + 1)/n со знаменателем n, больше первого отношения, оказывается больше и второго.] Отсюда заключаем, что
AC/AB = AE/AD.
Так же точно можно выяснить и следующие равенства:
AB/BC = AD/DE, AC/BC = AE/DE, AB/AC = AD/AE, BC/AC = DE/AE.
Для выяснения этих равенств надо поступать так же, как выше, но делить на n равных частей не отрезок AB, но BC и затем AC. Каждое из полученных равенств называется пропорциею.
Если построить еще MN || CE, то легко распространить тем же способом полученный результат и на новые отрезки. Тогда, напр., получим BC/CM = DE/EN и т. д.
Отсюда имеем:
Если стороны угла пересечь параллельными, то отношение двух каких-либо отрезков на одной стороне угла равно отношению двух соответствующих отрезков на другой стороне угла.
То же свойство выражают короче:
Если стороны угла пересечь параллельными, то отрезки на одной стороне угла пропорциональны соответствующим отрезкам на другой.
Слово «пропорциональны» надо понимать в том смысле, что отношение всякой пары отрезков на одной стороне равно отношению соответствующей пары отрезков на другой.
Это определение пропорциональности совпадает с тем, которое известно из арифметики. В самом деле, возьмем одну из наших пропорций, напр.,
AB/BC = AD/DE.
Отсюда легко увидать: 1) если AB > BC, то и AD > DE, т. е. с увеличением одной величины - отрезки на каждой прямой можно рассматривать, как величину - другая также увеличивается: 2) если, напр., AB = 3BC, то AB/BC = 3 и, следовательно, AD/DE = 3, откуда AD = 3DE, т. е., если одна величина увеличивается в несколько раз, то и другая увеличивается во столько же раз.
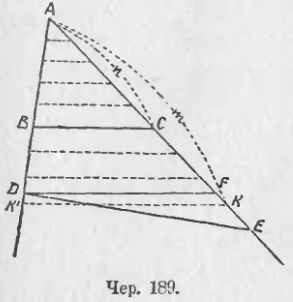
176. Пусть теперь ∠A (чер. 189) пересечен не параллельными прямыми BC и DE. Сравним, напр., отношения AD/AB и AE/AC. Построим DF || BC и разделим AC на такие равные части, чтобы каждая из них была меньше отрезка FE, и станем эти части откладывать на отрезке CE. Тогда конец хотя бы одной такой части попадет куда-либо между точками F и E (ибо каждая часть < FE), – пусть K есть конец одной из таких частей. Положим, что пришлось AC разделить на n равных частей и что таких частей от A до K уложилось m. Тогда
AK/AC = дроби m/n, но AK/AC < AE/AC
(ибо последующие члены одинаковы, а AK < AE), следовательно,
дробь m/n < AE/AC.
Построив через концы отложенных частей ряд параллельных (на чертеже даны пунктиром), последнею из которых есть KK', мы увидим, что точка K' придется вне отрезка AD, что AB разделится на n равных частей и что таких частей на AK' уложится m. Поэтому
AK'/AB = дроби m/n, но AK'/AB > AD/AB
(ибо последующие члены одинаковы, а AK' > AD), следовательно,
дробь m/n > AD/AB.
Мы видим, что здесь удалось найти дробь, которая меньше одного из отношений и больше другого; поэтому наши отношения не равны, а именно AD/AB < AE/AC.
Добавление. При нашем способе построения отрезков и при том порядке, в каком мы их берем для составления отношений, то из двух отношений оказывается меньше, члены которого расположены на стороне угла, более близкой к точке пересечения непараллельных BC и DE.
Если рассматривать отношения, обратные предыдущим, т. е. AB/AD и AC/AE, то имели бы, что AB/AD > AC/AE, т. е. то отношение было бы больше, члены которого располагаются на прямой, более близкой к точке пересечения прямых BC и DE.
177. Предыдущими признаками можно пользоваться для узнавания, равно ли отношение одной пары отрезков отношению другой пары. Пусть, напр., имеем 4 отрезка a, b, c и d (чер. 190). Узнаем, равно ли отношение отрезка a к отрезку b (т. е. a/b) отношению отрезков c и d (т. е. c/d). Для этой цели построим какой-либо ∠O и на его сторонах построим отрезки OA = a, OB = b, OC = c и OD = d. Построим затем прямые AC и BD: если AC || BD, то a/b = c/d, если AC не || BD, то a/b не равно c/d (если, например, как то приблизительно имеет место на чертеже, прямые AC и BD пересекаются в какой-либо точке, более близкой к OD, чем к OB, то c/d > a/b).
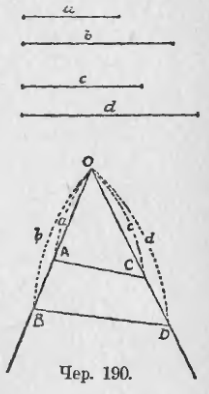
Добавление. Пусть оказалось, что AC || BD. Тогда a/b = c/d или b/a = d/c или, на основании п. 175, (b – a)/b = (d – c)/d (т. е. AB/OB = CD/OD) и т. п.
178. Если 4 данных отрезка a, b, c и d таковы, что, напр., a/b = c/d, то эти 4 отрезка составляют пропорцию, или мы имеем 4 пропорциональных отрезка. Пропорции, членами которых являются отрезки, обладают свойствами, сходными со свойствами пропорций, членами которых служат числа. Покажем, напр., что в пропорции
a/b = c/d (1)
где a, b, c и d суть отрезки, можно переставлять средние члены, т. е., что из предыдущей пропорции вытекает другая, а именно
a/c = b/d (2)
Для этого на сторонах угла O (чер. 191) отложим члены пропорции (1): OA = a, OB = b, OC = c и OD = d и построим прямые AC и BD.
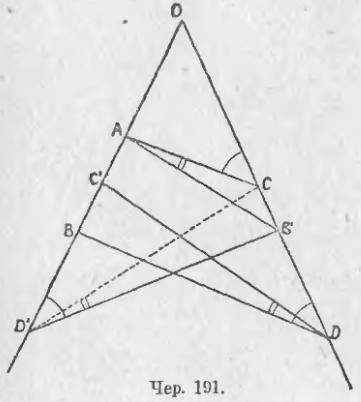
Так как пропорция (1) справедлива, то AC || BD. Отложим еще: OC' = OC = c, OD' = OD = d, OB' = OB = b, и построим прямые AB', DC', D'B' и D'C.
Тогда будем иметь ∠OCA = ∠ODB (ибо AC || BD) = ∠OD'B' (ибо ∆OBD = ∆OB'D' — у этих треугольников OB' = OB, OD' = OD и ∠O общий). Отсюда следует, что ∠ACB' + ∠AD'B' = 2d (ибо ∠AD'B' = ∠OCA), т. е. около четырехугольника ACB'D' можно описать круг (этот круг на чертеже не дан). Поэтому углы CAB' и CD'B' суть углы, вписанные в этот круг и опирающиеся на одну и ту же дугу CB', откуда заключаем, что ∠CA' = ∠CD'B', но ∠CD'B' = ∠C'DB, ибо ∆CD'B' = ∆C'DB (из равенства ∆OBD и ∆OB'D' вытекает, что BD = B'D'; также из равенства ∆OCD' и ∆OC'D вытекает, что DC' = D'C и, наконец, BC' = B'C, ибо BC' = OB – OC', а B'C = OB' – OC), следовательно, ∠CAB' = ∠C'DB. Теперь ∠CB'A является внутренним углом ∆CAB', а ∠OCA есть внешний угол для этого же треугольника.
Поэтому ∠CB'A или ∠OB'A = ∠OCA – ∠CAB'.
Далее непосредственно видим ∠ODC' = ∠ODB – ∠C'DB.
Но мы видели, что ∠OCA = ∠ODB и ∠CAB' = ∠C'DB, откуда следует, что ∠OB'A = ∠ODC', т. е., что AB' || C'D.
Поэтому имеем право написать пропорцию
OA/OC' = OB'/OD или a/c = b/d,
что и доказывает возможность переставлять средние члены пропорции. (Это доказательство заимствовано из D. Hilbert. Grundlagen der Geometrie.)
179. Чтобы лучше усвоить мысль, выраженную в п. 173, рассмотрим здесь еще пример.
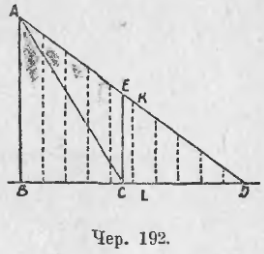
Пусть (чер. 192) через точку A построены: AB ⊥ BD и наклонные AC и AD. Сравним отношение наклонных с отношением их проекций, т. е. AC/AD с BC/BD. Построим прямую CE || BA; затем разделим AD (большую наклонную) на столько равных частей, чтобы каждая часть была меньше разности между AC и AE (AC > AE, что видно из ∆ACE, где ∠E тупой). Называя это число равных частей, на которые делим AD, через n, имеем:
AC – AE > 1/n AD.
Поэтому, если на AC укладывается таких частей m с остатком, то на AE их уложится по крайней мере на одну меньше, т. е. m таких частей составят отрезок больший, чем AE.
Разделив AD на указанные равные части, мы найдем отрезок AK, больший чем AE и равный m/n AD. Построив через точки деления ряд параллельных перпендикуляру AB, найдем, что BD разделится на n равных частей и получим отрезок BL = m/n BD, причем BL > BC. Итак, имеем:
BL = m/n BD, или BL/BD = m/n
но BC < BL, поэтому BC/BD < BL/BD, или
дробь m/n > BC/BD.
Согласно условию на наклонной AC тех частей, на которые разделена AD, укладывается m с остатком, т. е.
AC > m/n AD или AC/AD > m/n или дробь m/n < AC/AD.
Итак, нам удалось найти такое число m/n, что оно больше отношения проекций (BC/BD), и меньше отношения наклонных (AC/AD), откуда заключаем, что
AC/AD > BC/BD.
(Отношение наклонных больше отношения их проекций).
