7. На плоскости помещается множество точек и прямых. Принимают, что можно на плоскости строить точки и прямые; на практике для построения прямой употребляется линейка.
Прямая тянется без конца в обе стороны. На чер. 4 построена прямая AB; воображением можно продолжить ее без конца в обе стороны. Если построить какую-либо точку, напр., точку O, на прямой CD (чер. 4), то прямая разделится на 2 части: одна часть тянется от точки O вправо без конца, а другая – от точки O влево без конца. Каждая из этих частей называется лучом. Здесь имеем 2 луча: луч OD и луч OC.
Мы можем через каждую точку построить бесчисленное множество лучей.
Если возьмем на прямой 2 точки, напр., на прямой KL (чер. 4) точки E и F, то часть прямой линии между этими точками называется отрезком. На чертеже имеем отрезок EF.
8. Сравнить 2 данных отрезка AB и CD (чер. 5).
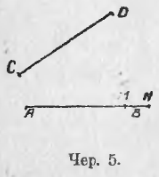
Перенесем отрезок CD так, чтобы точка C попала в A, и вращаем его около точки A до тех пор, пока отрезок CD не пойдет по отрезку AB. Когда этого достигнем, заметим, куда попадет точка D: если она попадет в B, то наши отрезки равны; если D попадет куда-либо между точками A и B (напр., в M), то отрезок CD считается меньше отрезка AB, и если точка D попадет за точку B (напр., в N), то отрезок CD больше отрезка AB.
«Сравнить» два отрезка понимаем в смысле установить, равны ли они или один больше другого.
9. Найти сумму двух данных отрезков.
Взяты два отрезка AB и CD (чер. 6); надо сложить эти отрезки.
Для этого переносим отрезок CD так, чтобы точка C попала в B, и затем вращаем его около B до тех пор, пока он не пойдет по продолжению отрезка AB. Отметим, куда попадет точка D; если она попадет в K, то отрезок BK = CD и AK = AB + BK или AK = AB + CD.
Всякий отрезок можно разбить промежуточными точками на сумму нескольких слагаемых; напр.:
AB = AC + CD + DE + EF + FB (чер. 7)
Для нас ясно, что сумма отрезков не изменяется от перестановки слагаемых.
10. Найти разность двух отрезков.
Даны два отрезка AB и CD (чер. 8); надо из большего отрезка AB вычесть меньший CD.
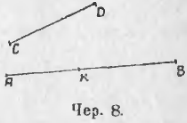
Переносим отрезок CD так, чтобы точка D попала в точку B, и станем вращать его около B до тех пор, пока он не пойдет по направлению BA; отметим, когда этого достигнем, куда попадет точка C. Если C попадет в K, то KB = CD и AK = AB – KB или AK = AB – CD.
Можно данный отрезок умножить на 2, на 3, на 4 и т. д., т. е. повторить его слагаемым 2, 3 и т. д. раз.
Из пп. 8-10 нам важно усвоить, что 1) к отрезкам, как и к числам, приложимы понятия: «равно», «больше» и «меньше»; 2) понятия о «сумме и разности двух отрезков» имеют вполне определенный смысл.
На практике для построения отрезка, равного данному, пользуются циркулем.
11. Упражнения. 1. Назвать слагаемые отрезки и их сумму в каждом из следующих изображений; записать (чер. A).
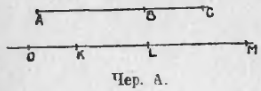
2. На тех же чертежах указать, какой отрезок можно считать разностью двух других отрезков; записать.
3. Данный отрезок разбить на 2, на 3, на 4 слагаемых; записать.
4. Данный отрезок представить, как разность двух других отрезков.
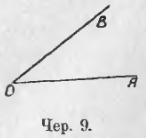
12. Мы можем построить фигуру, состоящую из двух лучей, исходящих из одной точки, – такая фигура называется углом. На чер. 9 изображен угол, состоящий из лучей OA и OB, исходящих из точки O. Эта точка называется вершиною угла, а каждый луч называется его стороною. Слово «угол» заменяется знаком ∠. Угол называется тремя буквами, из которых одна ставится при вершине, а две другие где-либо на сторонах угла, – буква при вершине ставится в середине названия угла. На чер. 9 имеем ∠AOB или ∠BOA; иногда угол называют одной буквою, поставленной при его вершине, говоря ∠O. Стороны угла (лучи) надо считать идущими без конца.
Особенный случай угла представится тогда, когда его стороны составляют одну прямую линию; такой особенный угол называют выпрямленным или развернутым углом (на чер. 12 изображены выпрямленные углы AOB и A1O1B1).
Каждый угол делит плоскость на 2 части, на две области. Одну из этих частей называют внутреннею областью угла и говорят, что она лежит внутри угла, а другую называют внешнею областью угла и говорят, что она лежит вне угла. Какую именно из этих двух частей называть внешнею областью, а какую внутреннею, – дело условия. Следует всякий раз отмечать как-либо внутреннюю, напр., область. Мы будем отмечать внутреннюю область угла кривыми линиями, начерченными на внутренней области между сторонами угла; на чер. 10 отмечены внутренние области углов ABC, DEF и выпрямленного ∠KLM.
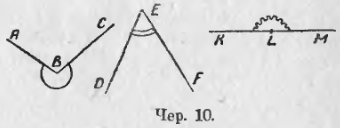
Полезно вырезать углы из листа тонкого картона: кусок картона является грубым изображением части плоскости; начертив на нем два луча, исходящих из одной точки, и разрезав этот кусок по сторонам начерченного угла, мы разделим кусок картона на 2 части; возьмем одну из этих частей, про которую хотим считать, что она лежит внутри угла, а другую удалим, – тогда будем иметь модель угла вместе с его внутреннею областью. Для правильного толкования этой модели надо иметь в виду, что кусок картона есть изображение лишь части плоскости, а сама плоскость тянется без конца.
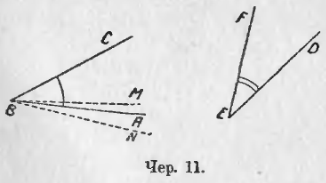
13. Сравнить два данных угла ∠ABC и ∠DEF (чер. 11).
«Сравнить» два угла значит установить, равны ли эти углы, или один больше другого. Для этого мы станем накладывать один угол на другой так, чтобы их внутренние области пошли друг по другу: если при этом окажется, что можно достигнуть того, чтобы вершины и стороны наших углов совместились, то мы говорим, что эти углы равны; если же вершины и по одной стороне у наших углов совпадут, а другие стороны не совпадут, то углы не равны, и меньшим мы читает тот, внутренняя область которого уложится на внутренней области другого.
Упражнение. Вырезать из бумаги модели углов вместе с их внутренними областями и, накладывая эти модели друг на друга, установить возможность случаев, описанных выше; вырезав модель одного угла, вырезать затем модель угла ему равного и модели углов ему не равных (большего или меньшего).
Обратимся к углам ABC и DEF (чер. 11); внутренняя область каждого из них на чертеже отмечена. Переносим ∠DEF так, чтобы его вершина E попала в точку B и его сторона EF пошла бы по стороне BC, – тогда внутренние области углов расположатся одна по другой. Если сторона ED пойдет при этом по стороне BA, то ∠DEF = ∠ABC; если сторона ED пойдет внутри ∠ABC, напр., по лучу BM, то ∠DEF < ∠ABC (здесь внутренняя область угла DEF уляжется на внутренней области ∠ABC, и еще останется незанятой область ABM); если сторона ED пойдет вне ∠ABC, напр., по лучу BN, то ∠DEF > ∠ABC.
Полезно повторить те же рассуждения для углов ABC и DEF (с отмеченными внутренними областями), данных на чер. 11 bis.
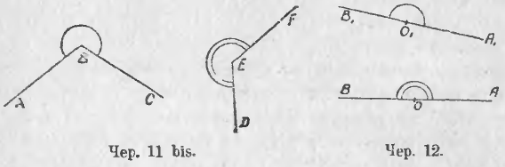
Применим изложенный способ сравнения двух углов к двум выпрямленным углам. Пусть имеем 2 выпрямленных угла ∠AOB и ∠A1O1B1 (чер. 12), внутренние области которых на чертеже отмечены. Наложив один из этих углов на другой так, чтобы вершина O1 одного попала в вершину O другого и чтобы сторона O1A1 одного пошла по стороне OA другого, мы придем к заключению, что и другие стороны этих углов O1B1 и OB совпадают, так как линии A1O1B1 и AOB суть прямые, положение которых определяется двумя точками. (Говорят иногда: «OB есть продолжение OA» вместо того, чтобы говорить, что линия AOB есть прямая). Поэтому приходим к заключению:
Все выпрямленные углы равны между собою.
14. Выпрямленный ∠AOB (чер. 12) делит плоскость на 2 области, на внутреннюю и внешнюю. Если перегнуть плоскость по прямой AOB, то обе эти части придут в совпадение. Поэтому можно принять, что внутренняя и внешняя области у выпрямленного угла равны между собою.
Если имеем какой-либо невыпрямленный угол, напр., ∠DEF (чер. 11 или чер. 11 bis), то, продолжив одну его сторону, напр., сторону DE (на чертежах продолжений не начерчено), мы увидим, что о нашем угле можно установить, что он или меньше выпрямленного (чер. 11), или больше его (чер. 11 bis); зависит это от того, какую из двух частей плоскости принять за внутреннюю область угла. Обычно выбирают внутреннюю область угла так, чтобы этот угол оказался меньше выпрямленного, причем условимся в таком случае не отмечать внутренней области угла. Иногда происхождение угла укажет, что за внутреннюю область надо счесть ту часть плоскости, что угол окажется больше выпрямленного. Эти случаи в дальнейшем будут иногда иметь место, и тогда мы уже должны отмечать внутреннюю область угла.
15. Найти сумму двух углов: ∠AOB и ∠PNM (чер. 13), или сложить ∠AOB и ∠PNM.
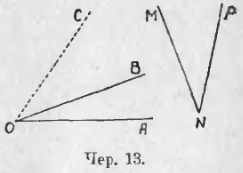
Здесь на чертеже не отмечены внутренние области углов; согласно замечанию предыдущего п., это значит, что их надо выбрать так, чтобы каждый угол был меньше выпрямленного, и мы ясно видим эти области.
Перенесем ∠PNM так, чтобы его вершина N совпала вершиною O угла AOB, и вращением около точки O достигнем того, чтобы сторона NP пошла по стороне OB; тогда внутренние области наших углов окажутся приложенными друг к другу, – это обстоятельство является существенным для сложения углов. Отметим затем, как пойдет сторона NM: пусть, напр., она пойдет по лучу OC. Тогда получим новый ∠AOС, который принимается за сумму двух данных углов. Мы можем написать:
1) ∠BOC = ∠PNM, 2) ∠AOC = ∠AOB + ∠BOC
и 3) (на основании 1) ∠AOC = ∠AOB + ∠PNM.
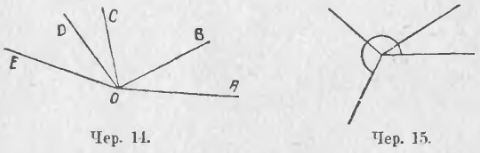
Так же можно складывать несколько углов; можно разбивать данный угол на несколько слагаемых. На чер. 14 имеем:
∠AOE = ∠AOB + ∠BOC + ∠COD + ∠DOE.
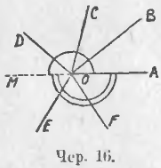
Легко построить два или несколько приложенных друг к другу углов, чтобы сумма их оказалась равна выпрямленному углу. Возможно, что сумма нескольких углов окажется больше выпрямленного угла (чер. 15), внутреннюю область этой суммы следует отметить.
Возможен еще особый случай сложения углов, когда внутренние области слагаемых углов покрывают собою, когда их приложат друг друга, всю плоскость. На чер. 16 имеем такие углы: ∠AOB, ∠BOC, ∠COD, ∠DOE, ∠EOF и ∠FOA. В этом случае, построив луч OM, являющийся продолжением луча OA, видим, что сумма наших углов состоит из двух выпрямленных углов: 1) выпрямленный ∠AOM, внутренняя область которого отмечена одною кривою линиею, и 2) выпрямленный ∠AOM, внутренняя область которого отмечена двойною кривою линиею. Здесь мы имеем:
∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOF + ∠FOA = 2 выпрямленным углам.
Говорят: Сумма всех последовательных углов, окружающих точку, равна двум выпрямленным углам.
Если имеются слагаемые углы еще, кроме построенных на чер. 16, то их придется прикладывать к прежним опять по первому выпрямленному углу, и тогда сумма получается больше двух выпрямленных углов, равная трем выпрямленным углам, больше трех выпрямленных углов и т. д.
16. Найти разность двух углов: ∠AOB и ∠MNP (чер. 17), или вычесть ∠MNP из ∠AOB, полагая, что ∠MNP < ∠AOB.
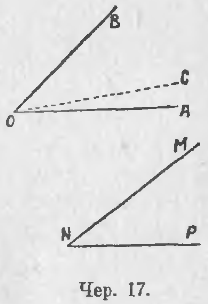
Перенесем ∠MNP так, чтобы его вершина N попала в вершину O угла AOB; вращением около точки O достигнем затем, чтобы сторона NM пошла по стороне OB, причем внутренние области этих углов расположатся одна на другой. Пусть сторона NP пойдет по лучу OC; тогда получим новый ∠AOC, о котором знаем, что ∠AOC + ∠COB = ∠AOB, откуда, согласно определению вычитания, как действия обратного сложению, получим:
∠AOC = ∠AOB – ∠COB,
но ∠COB = ∠MNP; поэтому
∠AOC = ∠AOB – ∠MNP.
Из пп. 13-16 мы должны усвоить мысль, что к углам, как и к отрезкам, приложимы понятия: больше, меньше, равно, и что понятия о сумме и разности двух углов имеют определенный смысл.
17. Упражнения. 1. Построить два приложенных друг к другу угла, назвать их буквами, указать их сумму и записать сложение этих углов.
2. На том же чертеже указать, что один из углов есть разность двух других; записать его.
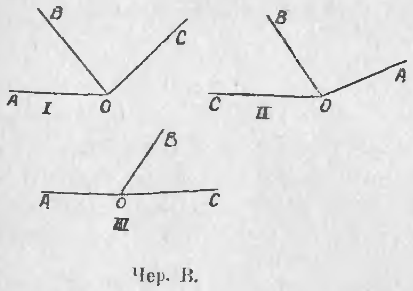
3. На следующих чертежах (см. чер. B) ∠AOB выразить разностью двух других углов.
4. Данный угол разбить на 2, на 3, на 4 слагаемых; всякий раз записывать это; сделать то же самое с выпрямленным углом.
5. Данный угол представить в виде разности между выпрямленным и каким-либо другим углом. Какое построение необходимо для этого?
6. Производить сложение и вычитание углов, пользуясь моделями углов, вырезанными из бумаги.
18. В дальнейшем мы часто будем нумеровать углы, чтобы, называя их нумерами, сократить письмо. Нумера углов будем писать внутри каждого угла около вершины.
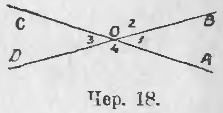
Построим ∠AOB (чер. 18) и будем называть его ∠1. Дополним этот угол до выпрямленного. Задача имеет два решения: построим луч OC, служащий продолжением луча OA; тогда получим ∠BOC или ∠2, удовлетворяющий требованию, так как видим, что
∠1 + ∠2 = выпрямленному углу.
Здесь мы имеем пример сложения двух углов, когда сумма равна выпрямленному углу, – такие углы называют смежными: ∠1 и ∠2 суть смежные углы. Чтобы 2 угла можно было назвать именем «смежные», надо, чтобы 1) они были приложены друг к другу и 2) чтобы их сумма равнялась выпрямленному углу, или, что то же самое, чтобы эти углы имели общую вершину (у углов 1 и 2 общая вершина O), одну общую сторону (у наших углов общая сторона OB) и чтобы две другие стороны являлись продолжением одна другой (OC есть продолжение OA).
Второе решение нашей задачи получится, если продолжить сторону OB, – пусть OD есть продолжение OB; тогда получим еще ∠AOD или ∠4, смежный с ∠1. Назовем еще полученный угол COD через ∠3.
Исследуем 2 полученных решения нашей задачи, т. е. ∠2 и ∠4. Мы видим особенность расположения ∠2 и ∠4: у них общая вершина O, стороны одного из них являются продолжениями сторон другого, а именно OC есть продолжение OA и обратно, и OB есть продолжение OD и обратно, – такие два угла называются вертикальными.
Затем мы знаем, что и ∠2 и ∠4 дополняют каждый в отдельности ∠1 до выпрямленного; отсюда заключаем, что
∠2 = ∠4.
Вот более подробное изложение последнего соображения. Согласно построению, мы имеем:
1) ∠1 + ∠2 = выпрямленному углу;
2) ∠1 + ∠4 = выпрямленному углу.
Мы видим, что оба сложения ведут к одинаковой сумме (все выпрямленные углы ведь равны между собою), и, кроме того, одно слагаемое (а именно ∠1) в обоих сложениях одно и то же; отсюда заключаем, что и другие слагаемые должны быть равны между собою, т. е. ∠2 = ∠4.
Если построить две пересекающихся прямых линии, то получим две пары вертикальных углов. На чер. 18 имеем прямые AC и BD, одна пара вертикальных углов есть ∠2 и ∠4, а другая ∠1 и ∠3. Все предыдущее применимо к каждой паре вертикальных углов; напр., для пары ∠1 и ∠3 имеем, что каждый из них дополняет ∠2 до выпрямленного, следовательно, ∠1 = ∠3. Поэтому имеем теорему:
Вертикальные углы равны между собою.
Упражнение. Построить через точку три прямых и указать полученные вертикальные углы; записать их равенство.
