206. Мы знаем (п. 175), что если ∠A (чер. 203 или 204) пересечь двумя параллельными KL и BC, то отношение двух любых отрезков на одной стороне этого угла равно отношению двух соответствующих отрезков на другой (напр., AK/KB = AL/LC; AB/AK = AC/AL и т. д.). Но мы видим, что у нас получились еще отрезки на самих параллельных, а именно KL и BC. Возникает вопрос, нельзя ли из отрезков AL, LC и AC, лежащих на одной стороне нашего угла A, выбрать такие два, чтобы их отношение равнялось отношению отрезков KL и BC.
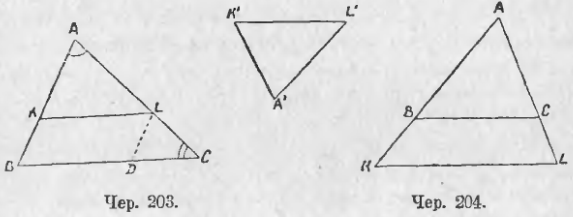
Для этой цели мы прежде всего отрезок KL перенесем на прямую BC, для чего надо построить LD || AB; тогда BD = KL. Тогда вместо отрезков KL и BC мы можем рассматривать отрезки BD и BC, которые расположены на стороне CB угла C. Так как ∠C оказался пересеченным двумя параллельными, а именно прямыми AB и LD, то, применяя п. 175 к углу C, мы найдем
BD/BC = AL/AC или KL/BC = AL/AC.
Вопрос решен: удалось найти два отрезка AL и AC на стороне AC так, что их отношение = KL/BC. Зная еще, что AK/AB = AL/AC, мы можем теперь написать равенства:
AK/AB = AL/AC = KL/BC.
Рассматривая эти равенства, мы приходим к заключению, что ими связаны стороны двух полученных треугольников, а именно ∆AKL и ∆ABC. Возникает новый вопрос: не связаны ли как-либо и углы этих треугольников?
На последний вопрос ответ легко найти: ∠A у наших треугольников общий, ∠K = ∠B, как соответственные при параллельных KL и BC и секущей AB, и ∠L = ∠C, как соответственные при тех же параллельных, но при секущей AC.
Мы можем перенести ∆AKL (чер. 203) в другое место, или, что тоже самое, построить новый ∆A'K'L', равный ∆AKL; его стороны и углы будут соответственно равны сторонам и углам ∆AKL: AK = A'K', AL = A'L', KL = K'L', ∠A = ∠A', ∠K = ∠K', ∠L = ∠L'.
Тогда мы получим ∆A'K'L', находящийся в такой же зависимости с ∆ABC, как и ∆AKL:
1) у этих треугольников углы попарно равны: ∠A' = ∠A, ∠K' = ∠B, ∠L' = ∠C;
2) для сторон имеем пропорции:
A'K'/AB = A'L'/AC = K'L'/BC (1)
Надо обратить внимание, что две стороны каждого отношения не случайно соединены в одно отношение, – нельзя, например, написать A'L'/AB = A'K'/BC = K'L'/AC. Надо уметь находить те стороны, которые должны быть членами одного отношения. Проще всего это сделать по углам треугольников: можно подметить, что стороны каждого отношения в равенствах (1) лежат в треугольниках против равных углов (A'K' против ∠L и AB против равного этому угла C и т. д.). Принято называть те стороны, которые служат членами одного отношения, сходственными (сторона A'K' сходна со стороною AB, A'L' — с AC и K'L' — с BC), причем сходственные стороны расположены в наших треугольниках против равных углов.
Равенство (1) можно прочесть сокращенно словами:
Стороны треугольника ∆A'K'L' пропорциональны сходственным сторонам ∆ABC.
Слово «пропорциональны» означает: отношение одной пары сходственных сторон треугольников A'K'L' и ABC равно отношению другой пары и равно отношению третьей пары.
Треугольники, обладающие двумя найденными выше признаками, называются подобными. Для обозначения подобия треугольников употребляют знак ~. Мы получили: ∆AKL ~ ∆ABC и также ∆A'K'L' ~ ∆ABC.
Можно теперь установить:
Два треугольника называются подобными, если углы одного равны попарно углам другого и сходственные стороны их пропорциональны.
Замечание. Возьмем из равенства (1) лишь одно, например, A'K'/AB = A'L'/AC. Применяя сюда свойство п. 178, получим: A'K'/A'L' = AB/AC, т. е. отношение двух сторон одного треугольника равно отношению двух сходственных сторон другого треугольника, подобного первому.
207. Основной признак подобия треугольников. Согласно предыдущему п., мы можем построить бесчисленное множество треугольников, подобных данному: для этого надо данный треугольник пересекать различными прямыми, параллельными одной из его сторон, и затем, если угодно, переносить каждый получаемый треугольник в другое место плоскости. Во всех получаемых треугольниках углы остаются неизменными, а отношение какой-либо стороны одного к сходственной стороне данного (масштаб подобия) меняется. Поэтому возникает мысль, недостаточно ли для подобия двух треугольников только равенства их углов.
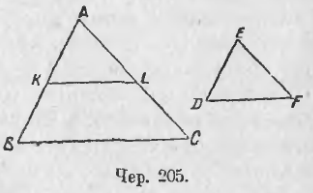
Построим 2 треугольника: ∆ABC и ∆DEF (чер. 205) так, чтобы ∠A = ∠E и ∠B = ∠D. Тогда прежде всего находим, что ∠C = ∠F (ибо сумма углов каждого треугольника = 2d).
Наложим ∆DEF на ∆ABC так, чтобы, напр., точка E попала в точку A. Тогда вращением около этой точки можно достигнуть в силу равенства ∠E = ∠A того, чтобы ED и EF пошли соответственно по AB и AC; сторона DF должна занять такое положение KL, чтобы ∠AKL = ∠D = ∠B и ∠ALK = ∠F = ∠C, т. е., чтобы KL || BC, так как получаются равные соответственные углы.
Отсюда заключаем, что ∆DEF можно получить построением предыдущего п. и, следов., что ∆DEF ~ ∆ABC. Итак, если два угла одного треугольника равны соответственно двум углам другого, то эти треугольники подобны.
208. Задача. Построить четвертый пропорциональный к трем данным отрезкам.
Пусть даны отрезки a, b и c (чер. 206); требуется построить такой 4-й отрезок x, чтобы имела место пропорция a/b = c/x.
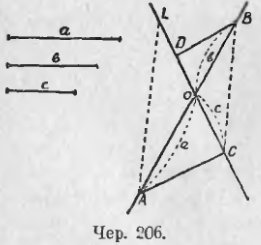
Строим две произвольных, пересекающихся в точке O, прямых AB и CD и откладываем от точки O на одной из них отрезки первого отношения: OA = a, OB = b (можно в одном, или в разных направлениях от точки O) и на другой прямой известный отрезок второго отношения OC = c. Затем соединим прямою концы тех отрезков, которые служат предыдущими членами нашей пропорции (если бы один из них не был известен, то надо соединить концы отрезков, служащих последующими членами данной пропорции); получим прямую AC, соединяющую концы отрезков a и c. Затем чрез точку B строим прямую BD || AC. Тогда поучим ∆OBD ~ ∆OAC (∠O = ∠O, как вертикальные и ∠C = ∠D, как внутренние накрест-лежащие, что достаточно по предыдущему п. для подобия наших треугольников). Отсюда имеем (п. 206) пропорциональность сходственных сторон:
OA/OB = OC/OD или a/b = c/OD,
отсюда вытекает, что искомый отрезок x = OD.
Если бы требовалось удовлетворить пропорции x/c = a/b, то надо было бы соединить точки B и C и через точку A построить AL || BD; тогда отрезок OL был бы искомым.
Замечание. Если мы построим отрезок x так, чтобы, напр., удовлетворилась пропорция x/c = a/b, то всякий другой отрезок x' не удовлетворит этой пропорции; если x' > x, то x'/c > x>c и, следовательно, x'/c > a/b, если x' < x, то x'/c < x/c и x'/c < a/b.
209. Другие признаки подобия треугольников. 1) Если две стороны одного треугольника пропорциональны двум сторонам другого и углы между ними равны, то эти два треугольника подобны.
Пусть имеем ∆ABC (чер. 207); возьмем произвольный отрезок ED и построим, согласно п. 208, отрезок x так, чтобы имела место пропорция x/AC = ED/AB. Наконец, построим ∆EDF так чтобы у него одною стороною служил отрезок ED, другою стороною отрезок EF = x и, наконец, чтобы ∠E = ∠A. Тогда ∆EDF и ∆ABC связаны между собою соотношениями:
1) ∠E = ∠A и 2) EF/AC = ED/AB.
Подобны ли эти треугольники?
Для получения ответа на этот вопрос надо лишь заметить, что мы можем построить треугольник, равный ∆EDF, иным, более простым способом. Для этого отложим на стороне AB отрезок AK = ED и построим KL || BC; тогда ∆AKL ~ ∆ABC (п. 197) и, след., AL/AC = AK/AB.
Так как AK = ED и так как можно лишь одним способом (замечание п. 208) удовлетворить пропорции x/AC = ED/AB, то отсюда заключаем, что EF = AL и что ∆AKL = ∆EDF. Поэтому ∆EDF наложением можно совместить с ∆AKL и, следовательно, ∆EDF ~ ∆ABC. Этим оправдывается признак пропорциональности, изложенный в начале этого п.
2) Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то эти треугольники подобны.
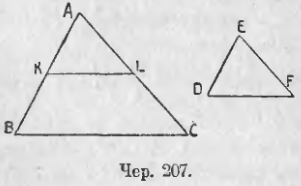
Пусть имеем ∆ABC (чер. 207); возьмем отрезок ED и построим согласно п. 208 два других отрезка x и y так, чтобы имели место пропорции: x/AC = ED/AB и y/BC = ED/AB. Построим затем по трем сторонам ED, x и y треугольник EDF (EF = x, DF = y).
Тогда ∆EDF и ∆ABC связаны между собою соотношениями:
1) EF/AC = ED/AB и 2) DF/BC = ED/AB
или, короче:
EF/AC = DF/BC = ED/AB.
Подобны ли эти треугольники?
Для решения этого вопроса заметим, что можно иным, более простым, способом построить треугольник, равный ∆EDF.
Для этого отложим на стороне AB отрезок AK = ED и построим KL || BC; тогда (п. 206) получим ∆AKL ~ ∆ABC и, след.,
AL/AC = KL/BC = AK/AB.
Так как отрезок AK = ED и так как, согласно замечанию п. 208, можно построить лишь один отрезок, удовлетворяющий пропорции x/AC = ED/AB, то заключаем, что AL = EF; также найдем, что KL = DF, откуда следует, что ∆EDF = ∆AKL, и наложением можно ∆EDF совместить с ∆AKL (иногда, может быть, придется для этого повернуть ∆EDF другою стороною). Поэтому ∆EDF ~ ∆ABC.
Этим оправдывается изложенный признак.
Подобным образом можно найти еще несколько признаков подобия, как вообще треугольников, так и каких-либо особых треугольников. Наприм., если гипотенуза и катет одного прямоугольного треугольника пропорциональны гипотенузе и катету другого, то эти треугольники подобны. Выяснение его справедливости основывается: 1) на замечании п. 208 и 2) на признаке равенства прямоугольных треугольников (п. 74, признак 4).
Замечание. В некоторых из следующих задач придется находить отношения отрезков, измеренных какою-либо единицею. Если, например, отрезок x = 7½ лин. един. и отрезок y = 3/10 лин. един. (линейная единица одна и та же), то, чтобы найти отношение отрезка x к отрезку y, надо выразить отрезок x числом, принимая за единицу отрезок y. Если y = 3/10 лин. единиц, то лин. един. = 10/3 * y и, следовательно,
x = (7½ * 10/3)y, откуда x/y = 7½ * 10/3 = 7½ : 3/10,
т. е. для наложения отношения отрезков, измеренных какою-либо одною единицею, надо найти отношение чисел, выражающих наши отрезки, а отношение чисел, как известно из арифметики, находится при помощи деления.
210. Упражнения.
1. Даны 2 прямоугольных треугольника; острый угол одного из них = 41°, а острый угол другого = 49°. Узнать, подобны ли эти треугольники.
2. Даны ∆ABC и ∆KLM (чер. 208) так, что ∠B = ∠M и AB = 15 дм., BC = 18 дм., ML = 12 дм. и MK = 10 дм. Подобны ли эти треугольники? Если они подобны, то вычислить сторону AC, зная, что сторона KL = 5½ дм.
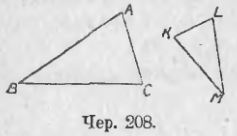
3. Даны ∆ABC и ∆KLM (чер. 208) так, что AB = 18 дм., BC = 20 дм., AC = 8 дм., KL = 6 дм., KM = 13½ дм., ML = 15 дм. Подобны ли эти треугольники? Как здесь узнать сходственные стороны?
4. В треугольниках ABC и KLM дано: AB = 16 дм., AC = 8 дм., BC = 20 дм., KL = 5 дм., MK = 10 дм. и ML = 12 дм. Подобны ли эти треугольники? Если не подобны, то как надо изменить сторону ML, чтобы треугольники оказались подобны?
5. Даны 2 подобных треугольника, стороны одного из которых равны соотв. 10, 14 и 16 дм. и большая сторона другого = 20 дм. Найти остальные 2 стороны второго треугольника.
6. Дан треугольник. Пользуясь способом п. 206, построить другой треугольник, подобный данному так, чтобы каждое отношение стороны нового треугольника к сходственной стороне второго было = ¾.
Сделать такое же построение, если вышеуказанное отношение должно равняться 2½.
211. Отношения высот и площадей подобных треугольников. Пусть имеем ∆ABC ~ ∆DEF (чер. 209). Следовательно, мы имеем: ∠A = ∠D, ∠B (∠ABC) = ∠E (∠DEF) и ∠C = ∠F (1) и
AB/DE = AC/DF = BC/EF (2)
Построим высоты BM и EN в наших треугольниках, опуская перпендикуляры на сходственные стороны; станем называть эти высоты сходственными. Тогда ∆ABM ~ ∆DEN, так как у них ∠A = ∠D на основании равенств (1) и ∠AMB = ∠DNE, как прямые углы (BM ⊥ AC и EN ⊥ DF), а этого достаточно для подобия наших треугольников (п. 207) и из их подобия получаем:
BM/EN = AB/DE.
На основании равенств (2) можем последнее равенство продолжить:
BM/EN = AB/DE = AC/DF = BC/EF,
т. е. отношение сходственных высот подобных треугольников равно отношению сходственных сторон.
Из ряда последних равных отношений обратим внимание на пропорцию.
BM/EN = AC/DF.
(Отношение сходственных высот = отношению оснований).
212. В п. 209 было указано, как находить отношение двух отрезков, измеренных одною и тою же единицею. Тоже относится и к нахождению отношения двух площадей, измеренных одною и тою же квадратною единицею: это отношение находится делением чисел, выражающих наши площади.
Мы будем в этом п., а равно во многих случаях и дальше под обозначением, например, AB понимать число, выражающее отрезок AB в каких-либо линейных единицах, также под обозначением «площадь ∆ABC» будем понимать число, выражающее площадь ∆ABC в квадратных единицах. При разборе одного вопроса все отрезки будут считаться измеренными одною и тою же линейною единицею, а все площади – соответствующими квадратными единицами.
Мы знаем (п. 201), что для измерения площади треугольника в квадратных единицах надо измерить его основание и высоту соответствующей линейною единицею и взять половину произведения полученных чисел.
Теперь, употребляя обозначение согласно вышесделанному условию, имеем для ∆ABC и ∆DEF (чер. 209)
площ. ∆ABC = (AC * BM) / 2 и площ. ∆DEF = (DF * EN) / 2.
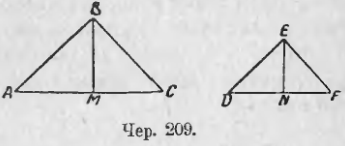
Найдем отношение площадей наших треугольников делением

т. е. отношение площадей двух треугольников равно произведению отношения их оснований на отношение их высот.
Примем теперь во внимание, что мы имеем дело с подобными треугольниками — мы считаем, что ∆ABC ~ ∆DEF.
Тогда из предыдущего п. имеем:
BM/EN = AC/DF.
Заменяя в формуле, выражающей отношение площадей треугольников, отношение высот равным ему отношением оснований, получаем:
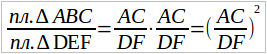
Можем также сказать, что это отношение = (AB/DE)2. Итак,
отношение площадей подобных треугольников равно квадрату отношения их сходственных сторон.
Этот результат согласуется с найденным в п. 160 (упражнения 5, 6 и 7).
Упражнение. Найти отношение площадей подобных треугольников, данных в п. 210 (упражнения 2, 3, 5 и 6).
213. Отношение площадей треугольников, имеющих по равному углу. Пусть в ∆ABC и ∆DEF (чер. 210) имеем ∠A = ∠D, а другие углы не равны. Тогда наши треугольники не подобны. Мы так же, как и в предыдущем п., построим высоты BM и EN этих треугольников и найдем делением отношение их площадей
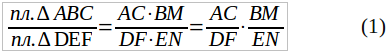
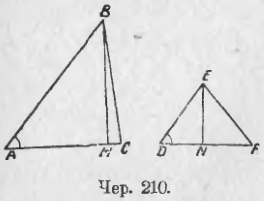
Далее находим ∆ABC ~ ∆DEF (∠A = ∠D по условию и ∠M и ∠N прямые); следовательно:
BM/EN = AB/DE (2)
Но теперь уже нельзя заменить отношение высот (BM/EN) отношением оснований (AC/DF), так как эти треугольники не подобны. Пользуясь (2) из (1) имеем:
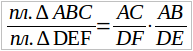
т. е. отношение площадей двух треугольников, имеющих по равному углу, равно произведению отношений сторон, составляющих эти углы.
Упражнение. Дан треугольник; построить другой треугольник так, чтобы один угол остался неизменным, а стороны, составляющие этот угол, увеличились одна в 2 раза и другая в 3 раза. Как увеличится его площадь? Ответ, легко находимый вычислением, желательно вычислить геометрически.
