214. Построение 4-го пропорционального отрезка, данное в п. 208, важно для решения некоторых задач на построение.
Задача. Данный параллелограмм превратить в равновеликий ему прямоугольник с данным основанием.
Обозначим основание данного параллелограмма через a, его высоту чрез h и данное основание искомого прямоугольника чрез b, а искомую высоту прямоугольника чрез x. Тогда мы знаем что площадь данного параллелограмма = ah, площадь искомого прямоугольника = bx, где на a, b, h и x надо смотреть, как на числа, полученные от измерения соответствующих отрезков одною и тою же линейною единицею. Согласно требованию задачи, имеем:
bx = ah,
откуда
x/a = h/b. (Другой способ решение дан в п. 159, зад. 1).
Так же решается (двумя способами) задача: превратить данный треугольник в равновеликий ему прямоугольник. Здесь придется в пропорции, которой должна удовлетворять искомая высота прямоугольника, взять не всю высоту треугольника, а ее половину.
215. Построим биссектор AD внутреннего угла A треугольника ABC (чер. 211). Возникает вопрос, как делит этот биссектор противолежащую сторону BC треугольника?
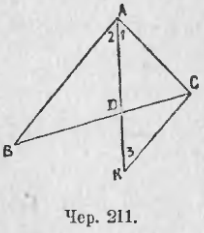
Для его выяснения продолжим AD и чрез точку C построим прямую CK || AB; пусть AD и CK пересекаются в точке K. Тогда получим два подобных треугольника: ∆ABD и ∆CDK (у них углы при точке K равны, как вертикальные, и ∠2 или ∠BAD = ∠3 или ∠DKC, как внутренние накрест-лежащие при параллельных AB и CK и секущей AK). Из их подобия имеем:
BD/DC = AB/CK (1)
Рассмотрим теперь ∆ACK. Мы знаем, что ∠1 = ∠2 (AD есть биссектор ∠A) и ∠2 = ∠3 (уже было выяснено), следовательно, ∠1 = ∠3, откуда заключаем, что CK = AC (против равных углов в треугольнике лежат равные стороны). Заменим в пропорции (1) отрезок CK равным ему отрезком AC; получим:
BD/DC = AB/AC,
т. е. биссектор внутреннего угла треугольника делит противоположную его сторону на такие 2 части, что их отношение равно отношению двух других сторон треугольника.
216. Подобным свойством обладает биссектор и внешнего угла треугольника. Построим биссектор AD внешнего угла при вершине A треугольника ABC (чер. 212); пусть он пересекает сторону BC в точке D.
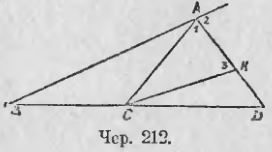
Пронумеруем углы, как на чертеже, цифрами 1, 2 и 3; тогда ∠1 = ∠2. Построим CK || AB, и пусть AD и CK пересекаются в точке K. Тогда ∆DAB ~ ∆DKC (согласно построению п. 206) и из их подобия имеем:
BD/CD = AB/CK (1)
∠3 = ∠2, как внутренние накрест-лежащие при параллельных CK и AB и секущей AK, а так как ∠1 = ∠2, то отсюда следует, что ∠1 = ∠3 и, следовательно, CK = AC (против равных углов лежат равные стороны в ∆ACK). Заменяя в пропорции (1) отрезок CK равным ему отрезком AC, найдем:
BD/CD = AB/AC.
Словами формулировать это труднее, чем в предыдущем п.:
Биссектор внешнего угла треугольника пересекает противоположную сторону (рассматриваемую, как бесконечная прямая) в такой точке. Что отношение ее расстояний от двух вершин треугольника, лежащих на этой стороне, равно отношению двух других сторон треугольника.
Говорят иногда вместо этого:
Биссектор внешнего угла треугольника делит противоположную сторону внешним образом в отношении, равном отношению двух других сторон, а биссектор внутреннего угла делит противоположную сторону внутренним образом в том же отношении.
217. Задача. Разделить данный отрезок внутренним и внешним образом в данном отношении.
Пусть дан отрезок AB (чер. 213); требуется найти сначала между точками A и B такую точку M, чтобы отношение ее расстояний от A и B равнялось данному числу m/n (вообще говоря, данное число — дробь; ее числитель = m и ее знаменатель = n; если данное число целое, то n = 1).
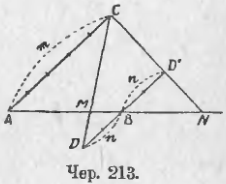
Для решения нашей задачи построим две прямых AC и BD под любым углом к AB, но непременно параллельных между собою, и отложим от A отрезок AC, содержащий m каких-либо частей, а от B в обратном направлении отложим отрезок BD, содержащий таких же n частей; тогда AC/BD = m/n. Соединив точки C и D, получим точку пересечения M прямых AB и CD, - она и есть искомая: ∆MAC ~ ∆MDB, следовательно, AM/MB = AC/BD = m/n.
Легко увидать, что другой такой точки между A и B найти нельзя: если мы передвинем точку M вправо (по направлению к B), то предыдущий член отношения AM/MB увеличится, от чего самое отношение также увеличится, а последующий член (MB) уменьшится, отчего самое отношение еще увеличится; точно так же передвинув M влево (по направлению к A), мы предыдущий член уменьшим, а последующий увеличим – от обеих причин отношение уменьшается.
Чтобы разделить отрезок AB внешним образом в отношении, равном числу m/n, или чтобы найти вне отрезка AB такую точку N, чтобы отношение расстояний этой точки от A до B было равно данному числу m/n (т. е., чтобы AN/BN = m/n), надо на прямой DD', которая параллельна прямой AC, от точки B отложить в том же направлении, в каком откладывали отрезок AC, отрезок BD', состоящий из n таких отрезков, которых в AC мы уложили m. Тогда, соединив точки C и D' и продолжив прямую CD' до пересечения с AB в точке N (если m = n или если m/n = 1, то CD' || AB и точки N не существует), увидим, что точка N и есть искомая: ∆ACN ~ ∆BD'N, следовательно, AN/BN = AC/BD' = m/n.
Здесь также можно увидать, что другой такой точки нет. Для этого надо лишь отношение AN/BN несколько преобразовать:
AN/BN = (AB + BN)/BN = AB/BN + 1.
(На нашем чертеже дробь m/n предполагается неправильной, т. е. m > n и поэтому точка N находится правее B; если бы дробь m/n была правильною, то точка N была бы расположена влево от A, и тогда, чтобы применить наше рассуждение к этому случаю, следует рассмотреть обратное отношение BN/AN).
Мы видим отсюда, что если точку N передвинуть, то отрезок BN изменится, а предыдущей член отношения (AB) н е изменится, а поэтому и все первое слагаемой AB/BN изменится; второе слагаемое 1 не изменится; следовательно, вся сумма AB/BN + 1 меняется с изменением BN, откуда и заключаем, что другой такой точки быть не может.
Замечание. Можно было бы данное отношение дать не числом, а отношением двух данных отрезков; тогда на прямых AC и DD' и следует откладывать эти отрезки.
4 точки A, B, M и N, расположенные на одной прямой, две из которых (A и B) были даны, а две другие были найдены при решении этой задачи, являются основою, из которой вытекает целый отдел геометрии, не входящий в обычный элементарный курс. Эти четыре точки, обладающие свойством, что AM/MB = AN/BN, называются гармоническими точками.
218. Если мы усвоим мысль, выясненную в предыдущем п., что отрезок допускает лишь одно его разделение в данном отношении внутренним образом и лишь одно — внешним образом, то отсюда найдем:
1) Если одна сторона треугольника разделена внутренним образом на 2 части, отношение которых равно отношению двух его других сторон и точка деления соединена с противоположною вершиною, то последняя прямая является биссектором внутреннего угла треугольника при этой вершине.
В самом деле, в данном отношении внутренним образом отрезок допускает лишь одно разделение, а то разделение, о котором идет здесь речь, производится, как мы знаем (п. 215), биссектором угла — следовательно, указанная прямая и есть биссектор угла.
2) Если одна из сторон треугольника разделена внешним образом на 2 части, отношение которых равно отношению двух его других сторон, то прямая, соединяющая точку деления с противоположною вершиною, должна быть биссектор внешнего угла при этой вершине (объяснение сходно с предыдущим, надо лишь сослаться на п. 216).
219. Пусть даны 2 точки A и B (чер. 214); тогда на прямой AB можно найти 2 точки (одну внутри отрезка AB, и другую — вне его) так, чтобы отношения расстояний каждой из них от A и B было равно данному числу, т. е., чтобы AM/MB = AN/BN = k, где k данное число (целое, дробное или даже иррациональное).
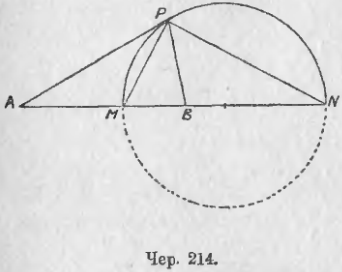
Возникает вопрос, не существует ли где-либо вне прямой такой точки P, чтобы отношение ее расстояний от A и B равнялось тому же числу k.
Допустим, что нам удалось найти такую точку P; тогда PA/PB = k, откуда имеем AM/MB = PA/PB и AN/BN = PA/PB (каждое из этих отношений равно числу k).
Мы видим, что у нас получился ∆APB, в котором сторона AB разделена в точке M внутренним образом, а в точке N внешним образом в отношении, равном отношению двух других его сторон, а это, как мы знаем, возможно лишь в том случае, когда PM и PN суть биссекторы: первый = внутреннего ∠P треугольника APB, а второй — его внешнего угла. Мы знаем (п. 62 упражнение 4), что они перпендикулярны между собою, т. е. ∠MPN = d. Следовательно, искомая точка P обладает свойством, что из нее отрезок MN виден под прямым углом, а такие точки, как знаем, расположены на круге, диаметр которого есть отрезок MN (пп. 134 и 135).
Отсюда заключаем:
Геометрическим местом точек, отношение расстояний которых от двух данных точек равно данному числу, служит круг, построить который мы умеем: надо отрезок, соединяющий две данных точки, разделить внутренним и внешним образом в отношении, равном данному числу, и полученные две точки принять за концы диаметра искомого круга.
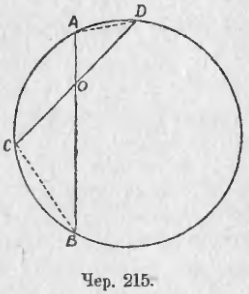
220. Возьмем внутри круга какую-либо точку O (чер. 215) и построим чрез нее две произвольных хорды AB и CD. Соединив затем точку A с D и B с C (можно A с C и B с D), получим ∆AOD ~ ∆OBC, так как углы при точке O равны, как вертикальные, ∠A = ∠C, как вписанные, опирающиеся на одну дугу BD, что достаточно для подобия треугольников. Поэтому имеем:
OB/OD = OC/OA.
Если мы теперь под обозначениями входящих сюда отрезков будем понимать числа, полученные от их измерения какою-либо единицею, то можем сюда применить свойство пропорции, взятое из курса арифметики (или алгебры): произведение крайних членов равно произведению средних; следовательно,
OA * OB = OC * OD,
т. е., если две хорды пересекаются внутри круга, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Так как хорды проведены чрез O произвольные, то произведение отрезков и третьей хорды должно быть такое же, следовательно:
произведение отрезков хорд, проходящих через точку, данную внутри круга, постоянно.
Впрочем, равенством
AO * OB = OC * OD
имеет и геометрический смысл: произведение OA * OB выражает площадь прямоугольника, стороны которого суть отрезки OA и OB, в соответствующих квадратных единицах; такой же смысл имеет и произведение OC * OD. Поэтому имеем:
Прямоугольники, сторонами каждого из которых служат отрезки хорды, проходящей через постоянную точку внутри круга, равновелики.
221. Возьмем теперь точку O вне круга и построим чрез нее касательную OA к кругу и несколько секущих OC, ON … (чер. 216). Соединив точку касания A касательной с точками B и C, где секущая OC пересекает круг, получим ∆OAC ~ ∆OAB, так как у них ∠O общий и ∠C = ∠OAB, потому что угол, составленный хордою и касательною, равен вписанному углу, опирающему на дугу, заключенную внутри того же угла (п. 133).
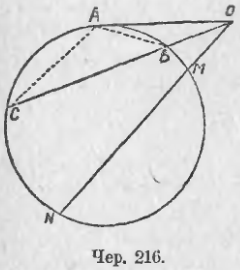
Из подобия этих треугольников имеем:
OC/OA = OA/OB
(стороны OC и OA лежат против углов OAC и OBA, стороны OA и OB — против углов ACO и OAB).
Эта пропорция читается:
Если из точки вне круга построить к нему касательную и секущую, то касательная является средним пропорциональным отрезком между всею секущею и ее внешнею частью.
Можно также применить сюда свойство пропорции: произведение крайних членов равно произведению средних, получим
ON * OM = OA2
т. е., если через точку вне круга проводить секущие, то произведение всей секущей на ее внешний отрезок постоянно и равно квадрату касательной, проведенной к кругу через ту же точку.
Здесь выражение «квадрат касательной» надо понимать в смысле «квадрат числа, полученного от измерения касательной линейною единицею».
Можно то же свойство выразить геометрически:
Прямоугольники, сторонами каждого из которых служат секущая, проведенная к кругу через определенную внешнюю точку, и ее внешний отрезок, равновелики между собою и равновелики квадрату, стороною которого служит касательная, проведенная к кругу в ту же точку.
222. Свойства двух предыдущих пп. можно выразить одинаково:
Если в плоскости круга возьмем какую-либо точку и чрез нее построим ряд прямых, то произведение отрезков каждой прямой от этой точки до точек пересечения этой прямой с кругом есть число постоянное (каждый отрезок выражен числом), зависящее только от круга и от положения точки, но не зависящее от того, какую прямую проводим через эту точку.
Указанное произведение как бы характеризует положение точки относительно круга и называется степенью этой точки относительно круга.
Мы впоследствии еще вернемся к этому понятию.
223. Упражнения.
- Периметр треугольника равен 45 дм., биссектор меньшего из его углов делит противоположную сторону на отрезки, равные 4 и 6 дм. Вычислить каждую из его сторон.
- Две хорды круга пересекаются внутри его так, что меньшие их отрезки равны 6 и 9 дм. Вычислить длину каждой хорды, если отношение этих хорд = ¾.
- Параллельные стороны трапеции равны соответ. 12 и 28 лин. един.; если продолжить непараллельные стороны до их пересечения, то одна из них увеличится от этого продолжения на 9, а другая на 6 лин. един. Вычислить не параллельные стороны трапеции.
- В трапеции построены диагонали: дна из них = 21 дм., а другая в точке пересечения разделилась на отрезки, равные 8 и 20 дм. Вычислить: 1) на какие отрезки разделилась другая диагональ и 2) параллельные стороны этой трапеции, если ее средняя линия = 21 дм.
- К кругу из внешней точки проведены секущая, внутренний отрезок которой = 36 дм., и касательная, которая в 2 раза больше внешнего отрезка секущей. Вычислить секущую и касательную.
- Показать, что отношение двух высот треугольника равно обратному отношению соответств. оснований (можно двумя способами: 1) при помощи подобия треугольников и 2) пользуясь уменьем измерять площадь треугольника).
- Построение четвертого пропорционального отрезка к трем данным можно выполнять без построения параллельных, а с помощью круга, на основании п. 220 или п. 221. Выполнить несколько таких построений.
- Обратно: если построены две пересекающихся прямых и от точки их пересечения отложены на каждой прямой в одном или в обратных направлениях по 2 отрезка таких, что произведение отрезков на одной прямой равно произведению отрезков другой, то 4 конца этих отрезков расположены на одном круге.
- Построить прямоугольник, имеющий одну данную сторону и равновеликий сумме двух данных треугольников, имеющих общее основание.
- Построить треугольник по стороне, по высоте, опущенной на эту сторону, и по другой высоте.
224. Теорема Птоломея. Пусть в круг вписан какой-либо четырехугольник ABCD (чер. 217); построим его диагонали AC и BD и построим еще прямую AK (точка K есть точка пересечения этой прямой с диагональю) так, чтобы ∠BAK = ∠DAC.
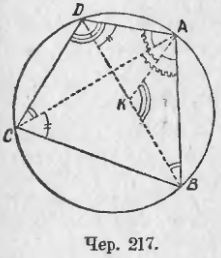
Рассмотрим ∆ABK и ∆ADC. У них по построению ∠BAK = ∠DAC и затем ∠ABK = ∠ACD, как вписанные, опирающиеся на одну дугу AD. Следоват., ∆ABK ~ ∆ADC. Отсюда имеем:
AB/AC = BK/DC
Применим сюда свойство: произведение крайних членов пропорции равно произведеню средних, имеем:
AC * BK = AB * DC (1)
Рассмотрим затем ∆AKD и ∆ABC. У них ∠DAK = ∠BAC (каждый из этих углов является суммою одинаковых слагаемых: общее слагаемое есть ∠KAC и равные слагаемые ∠DAC = ∠BAK), затем ∠ADK = ∠ACB, как вписанные опирающиеся на одну дугу AB. Следовательно, ∆AKD ~ ∆ABC. Поэтому имеем:
AD/AC = DK/BC,
откуда получаем:
AC * DK = AD * BC (1)
Сложив равенства (1) и (2) по частям (мы ведь рассматриваем здесь обозначения AB, AC и т. д., как числа), получим:
AC * BK + AC * DK = AB * DC + AD * BC
Вынесем в первой части число AC за скобку
AC (BK + DK) = AB * DC + AD * BC
и, замечая, что BK + DK = BD, получим:
AC * BD = AB * DC + AD * BC.
Это свойство читаем (сокращенно) словами:
Произведение диагоналей вписанного в круг четырехугольника равно сумме произведений его противоположных сторон.
Можно дать и геометрическое толкование этому:
Прямоугольник, сторонами которого служат диагонали вписываемого четырехугольника, равновелик сумме двух прямоугольников, сторонами каждого из которых служат две противоположные стороны четырехугольника.
225. Пусть построен прямоугольный треугольник ABC (чер. 218), ∠B = d. Построим еще BD ⊥ AC — опустим перпендикуляр из вершины прямого угла на гипотенузу — пронумеруем полученные углы: ∠A = ∠1, ∠ABD = ∠2, ∠DBC = ∠3, ∠C = ∠4.
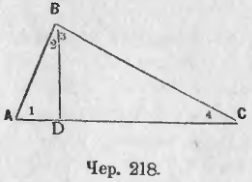
Тогда имеем: ∠1 + ∠2 = d (так как сумма острых углов прямоугольного треугольника ABD — угол при D прямой — равна прямому углу), с другой стороны ∠2 + ∠3 = d (так как ∠B прямой), отсюда заключаем, что ∠1 = ∠3; также найдем, что ∠2 = ∠4.
Рассмотрим теперь ∆ABD и ∆DBC; они, в силу найденных равенств углов, подобны; следовательно,
AD/BD = BD/DC
(AD лежит против ∠2 и ∆ABD, ему в ∆BDC = ∠4, против которого лежит сторона BD; члены второго отношения BD и DC суть стороны, расположенные против равных углов: BD в ∆ABD против ∠1 и DC в ∆BDC против ∠3).
Эту пропорцию, имея в виду, что у нее средние члены одинаковы, читаем: «перпендикуляр BD есть средний пропорциональный отрезок между отрезками AD и DC гипотенузы».
Рассмотрим затем ∆ABC и ∆ABD; они подобны, потому что у них ∠A общий и ∠B (∠ABC) = ∠D (∠ADB), как прямые углы. Отсюда имеем:
AC/AB = AB/AD
(AC и AB против прямых углов, AB и AD против равных углов ∠2 и ∠4).
Эту пропорцию прочтем: «Катет AB есть средний пропорциональных отрезок между всею гипотенузою AC и ее отрезком AD».
Также найдем, что ∆ABC ~ ∆DBC и отсюда:
AC/BC = BC/DC
Эта пропорция выражает свойство катета BC, такое же, какое только что было найдено для AB.
Соединяя все вместе, получим:
Если из вершины прямого угла прямоугольного треугольника опустить перпендикуляр на гипотенузу, то этот перпендикуляр есть средний пропорциональный между отрезками гипотенузы, а каждый из катетов есть средний пропорциональный между всею гипотенузою и ее отрезком, прилежащим к этому катету.
226. Предыдущим свойством, а также п. 216, пользуются для построения отрезка среднего пропорционального между двумя данными.
Пусть даны отрезки a и b (чер. 219); требуется построить такой отрезок x, чтобы имела место пропорция a/x = x/b.

Для этого откладываем отрезок AB = a и прилагаем к нему отрезок BC = b. Примем полученную сумму двух отрезков, отрезок AC, за диаметр и построим на нем круг (достаточно половину круга; его центр O расположен в середине отрезка AC). Затем через точку B строим BD ⊥ AC — точка D есть точка пересечения этого перпендикуляра с кругом. Тогда BD и есть искомый отрезок. В самом деле, соединив D с A и с C, получим прямоугольный треугольник ADC (∠ADC прямой, так как он вписанный и опирается на диаметр AC круга) и, следовательно, согласно предыдущему п., имеем AB : BD = BD : BC или a : BD = BD : b, откуда и заключаем, что x = BD.
Можно видоизменить это построение: сделать так, чтобы отрезок a был всею гипотенузою, а отрезок b — ее отрезком до перпендикуляра, опущенного на нее из вершины прямого угла. Строим AB = a (чер. 220) и на нем AC = b. Принимая AB за диаметр, строим круг и из точки C строим CD ⊥ AB. Тогда отрезок AD, служащий катетом прямоугольного треугольника ADB, есть средний пропорциональный между AB и AC, т. е. между a и b.
Также можно воспользоваться п. 207 для этого построения.
227. Предыдущее построение необходимо для решения многих задач. Вот некоторые из них:
1. Построить квадрат, равновеликий данному параллелограмму.
Называя сторону искомого квадрата через x, а основание и высоту данного параллелограмма чрез a и h, имеем:
x2 = ah, откуда a/x = x/h,
т. е. искомая сторона есть средний пропорциональный отрезок между основанием и высотой данного параллелограмма.
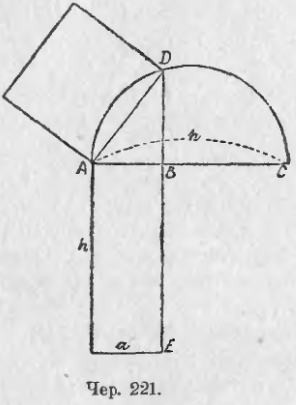
Если дан прямоугольник, то построение можно выполнить, как указано на чер. 221: продолжим сторону AB так, чтобы AC = h и принимая AC за диаметр, построим круг; продолжив сторону BE прямоугольника, получим точку D, соединив ее с A, получим сторону искомого квадрата, а затем и сам квадрат.
2. Построить круг, проходящий через две данных точки и касательный к данной прямой.
Пусть даны точки A и B и прямая KK' (чер. 222). Требуется построить круг, проходящий через A и B и касающийся прямой KK'. Точки A и B должны быть даны с одной стороны KK', - иначе задача невозможна.
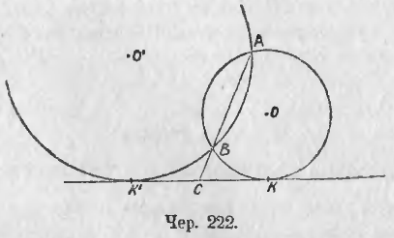
Легко найти точку касания искомого круга: соединим точки A и B и продолжим прямую AB до пересечения в точке C с KK'. Тогда точка касания K определяется из пропорции (п. 221)
CA/CK = CK/CB.
Отрезки CA и CB нам известны, мы можем на основании п. 226 построить средний пропорциональный к ним; отложив этот отрезок по прямой KK' от C, получим две точки K и K', каждая из которых дает по одному решению, - всего задача имеем 2 решения.
Центры искомых кругов O и O' найдутся, как точки пересечения перпендикуляра к AB через его середину и перпендикуляра к KK' из точки K (для O) или из точки K' (для O').
3. Построить круг, касающийся двух данных пересекающихся прямых и проходящий через данную точку.
Пусть даны прямые AB и AC, к которым должен касаться круг и точка D, через которую он должен проходить (чер. 223).
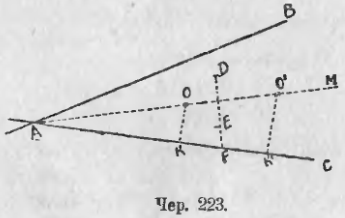
Задача приводится к предыдущей. Центр искомого круга лежит на биссекторе того угла, образуемого нашими прямыми, внутри которого лежит точка D. Построим точку E, симметричную с D относительно биссектора AM; тогда круг должен пройти и через точку E. Задача свелась к предыдущей. Мы должны отложить FK = FK', где FK есть средний пропорциональный отрезок между FD и FE. Центры двух кругов, удовлетворяющих требованиям, суть точки пересечения биссектора AM с перпендикулярами KO и K'O' к стороне AC.
