Прямая линия

Прямая линия есть кратчайшее расстояние между двумя точками.

Свойства прямой. a) Положение прямой линии вполне определяется теми двумя точками, между которыми она проведена.

Это свойство зависит от того, что b) между двумя точками можно провести только одну прямую линию, ибо между двумя точками существует только одно кратчайшее расстояние.

Определение прямой линии, вытекающее из непосредственного усмотрения ее свойства, некоторые называют аксиомой. Это понятие о прямой линии называют иногда основным.

В прямой линии нужно отличить ее положение и ее длину.

Прямую линию можно неопределенно продолжать в обе стороны.

Две точки определяют прямую линии не только в тех точках, которые лежат между ними, но и в тех точках, которые получаются, если неопределенно продолжать прямую линию в обе стороны.

c) Две прямые линии пересекаются в одной точке, ибо точка их пересечения находится на конце прямой линии.

d) Через одну точку можно провести бесчисленное множество прямых линий.

Все линии на чертеже 5 проходят через общую точку A.

 

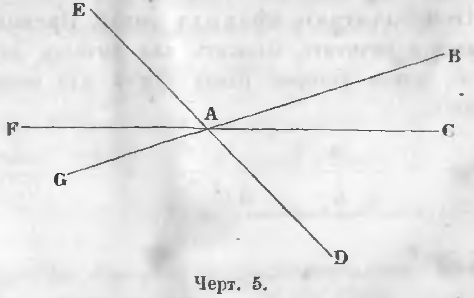
e) Если две прямые имеют две общие точки, то они совпадают всеми остальными точками.

f) Расстояние между двумя точками определяется длиной прямой линии, их соединяющей.

Равные прямые. Две прямые линии, имеющие одинаковую длину, называются равными. Линии AB с CD (черт. 6) будут равными линиями.

 

Равные прямые совпадают при наложении друг на друга.

Сравнение прямых линий

Чтобы сравнить две данные прямые AB и CD по длине (черт. 7) накладывают линию CD на линию AB так, чтобы точка C совпадала с точкой A.

 

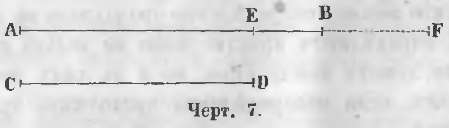
Здесь могут быть три случая:

1. Если точка D упадет в точку E, находящуюся между A и B, линия CD меньше AB.

2. Если точка D упадет в точку B, линия CD равна AB.

3. Если точка D упадет в точку F, находящуюся на продолжении линии AB, линия CD больше AB.

Сложение и вычитание прямых линий. Прямые линии можно складывать и вычитать. Сложить или вычесть линии значит найти линию, длина которой равна сумме или разности длин данных линий.

 

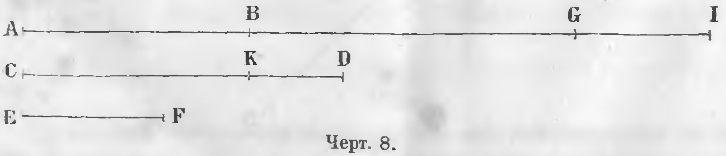
Чтобы сложить прямые линии AB, CD, EF (черт. 8), продолжают линию AB и от точки B откладывают линию BG, равную CD, от точки G линию GI равную EF. Линия AI равна сумме всех этих трех линий.

AI = AB + CD + EF.

Чтобы найти разность линий CD и AB, откладывают на линии CD от точки C линию CK, равную AB, тогда линия KD равна разности линий CD и AB.

KD = CD - AB.

Отношение двух прямых линий

Сравнивая две прямые линии по длине, определяют их взаимное отношение. При этом сравнении имеет значение линия, называемая общей мерой двух линий.

Общая мера двух линий есть такая линия, которая содержится целое число раз в обеих линиях.

При определении взаимного отношения двух прямых линий по длине, могут встретиться два случая:

1. Когда эти линии имеют общую меру.

2. Когда они ее не имеют.

В первом случае они называются соизмеримыми, во втором — несоизмеримыми. В первом случае отношение двух линий выражается каким-нибудь рациональным, т. е. целым или дробным числом; во втором оно не может быть точно выражено ни целым, ни дробным числом.

Если две прямые линии соизмеримы, то находят их общую меру.

Определение общей меры двух линий

Общая мера двух линий большей AB и меньшей CD (черт. 9) не может быть больше линии CD. Удостоверимся сначала, не будет ли меньшая линия CD этой общей мерой.

 

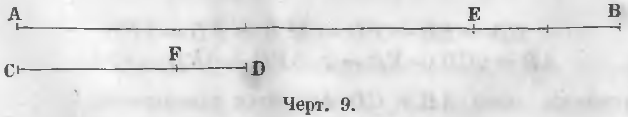
Для этого накладывают меньшую линию на большую и определяют, сколько раз она уложится в большей. Если она укладывается ровное число раз, например, m раз, тогда отношение двух линий выражается этим целым числом m.

Действительно, тогда

AB = m * CD и AB/CD = m.

Если же она не укладывается ровное число раз, то последовательно накладывают линию CD до тех пор, пока не получится остатка EB меньшего CD.

Положим, линия CD уложилась в AB два раза и получился еще остаток EB. Общая мера линий AB и CD не может быть более остатка EB.

Действительно, из равенства

AB = 2CD + EB

видно, что общая мера линий AB и CD должна содержаться равное число раз в линии EB. Она может или равняться линии EB или быть меньше ее.

Отсюда заключение:

Общая мера двух линий AB и CD должна быть общей мерой меньшей линии и остатка EB.

Отыскивая общую меру CD и EB, поступаем по предыдущему. Откладываем линию EB на линии CD до тех пор, пока не получится остатка FD, меньшего линии EB. Общая мера CD и EB будет по предыдущему заключению общей мерой EB и FD.

Линию FD снова откладываем по линии EB. Пусть линия FD отложится на линии EB ровно два раза, тогда линия FB и будет этой общей мерой.

Связь между линиями выразится рядом равенств:

AB = 2CD + EB
CD = EB + FD
EB = 2FD

откуда

CD = EB + FD = 2FD + FD = 3FD
AB = 2CD + EB = 2 * 3FD + 3FD = 8FD.

Отношение линий AB и CD выразится равенством:

AB/CD = 8FD/3FD = 8/3.

Мы видим, что при нахождении общей меры нужно поступать точно так же, как при нахождении общего наибольшего делителя между целыми числами. Отсюда

Правило нахождения общей меры двух линий. Чтобы найти общую меру, нужно меньшую линию наложить на большую, первый остаток на меньшую, второй остаток на первый, и поступить так до тех пор, пока последний остаток не уложится ровное число раз в предпоследнем.

Чтобы найти отношение двух линий, нужно при помощи общей меры выразить обе линии и потом найти частное этих выражений.

2-й случай: две прямые линии несоизмеримы. Если две линии несоизмеримы, мы никогда не получим такого остатка, который содержался бы в предпоследнем остатке целое число раз. В этом случае определяют отношение прямых линий с каким угодно приближением. Для этого разделив меньшую линию на n равных частей, накладывают это часть CE на большую линию AB (черт. 10). Положим, что эта часть повторяется в большей линии m раз и еще получается остаток FB меньше CE.

 

Из равенств

AB = mCE + FB
CD = nCE

имеем

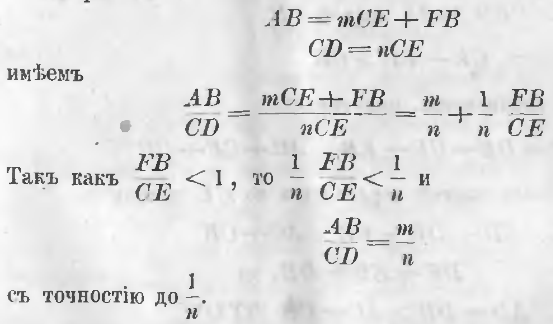
Так как n можно увеличивать произвольно, то и отношение длин двух прямых можно выразить с каким угодно приближением.

(См. о несоизмеримости диагонали квадрата с его стороной).

Измерение линий. Измерить линию значит найти ее отношение к другой линии, принятой за единицу. Это отношение называют длиной данной линии. Длина линии всегда выражается в каких-нибудь единицах.

Ломаные линии

Две линии ACB и ADB (черт. 11), соединяющие концы прямой AB, называются ломаными. При этом линия ACB называется внутренней, а линия ADB внешней ломаной линией.

 

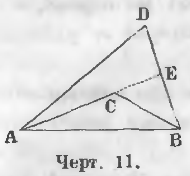
Теорема 1. Внешняя ломаная больше внутренней.

Даны две ломаные линии: внешняя ADB и внутренняя ACB (черт. 11).

Требуется доказать, что ADB больше ACB или

AD + DB > AC + CB.

Доказательство. Продолжим линию AC до пересечения с линией DB в точке E.

Линия ADE как ломаная больше прямой AE.

AD + DE > AC + CE

Ломаная линия CEB больше прямой CB

CE + EB > CB

Сложив эти неравенства, получим:

AD + DE + CE + EB > AC + CE + CB

Вычтя из обоих частей неравенства по CE, получим:

AD + DE + EB > AC + CB

Так как DE + EB = DB, то

AD + DB > AC + CB.

Что и требовалось доказать.

Теорема 2. Сумма пересекающихся частей ломаных больше суммы непересекающихся.

Даны пересекающиеся ломаные ABC и ADC (черт. 12), AD и BC их пересекающиеся части.

 

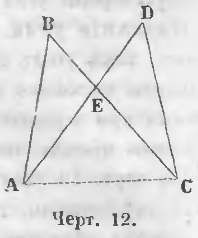
Требуется доказать, что

AD + BC > AB + DC.

Доказательство. Из того, что ломаная AEB больше прямой AB и ломаная CED больше прямой DC вытекают неравенства:

AE + BE > AB
ED + EC > DC

Сложив их, находим:

AE + BE + ED + EC > AB + DC

Так как

AE + ED = AD
BE + EC = BC

то

AD + BC > AB + DC

Что и требовалось доказать.