19. Если луч OA (чер. 19) вращается на плоскости около точки O по направлению, указанному стрелкою, и если он достигнет положения OB, то два положения вращающегося луча: начальное OA и конечное OB составят ∠AOB, внутреннею областью которого (она отмечена на чертеже) считаем ту часть плоскости, которую опишет вращающийся луч. Поэтому:
Угол можно рассматривать, как результат поворота луча около точки.

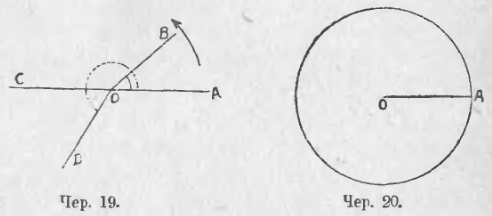
Если конечное положение луча окажется продолжением начального – на чертеже OC есть есть продолжение OA, – то результатом поворота луча явится выпрямленный угол. Если вращающийся луч еще повернется, то получим ∠AOD, больший выпрямленного угла; его внутрення область отмечена пунктирною кривою линиею. Продолжая еще вращение луча, можно получить угол, равный двум выпрямленным, больший двух выпрямленных, равный трем выпрямленным и т. д.

20. Если вращать на плоскости отрезок AO (чер. 20) около одного из своих концов, напр., около точки O, то другой конец A опишет замкнутую линию, называемую кругом или окружностью. Эта линия ограничивает определенную часть плоскости, называемую площадью круга (или окружности). Точка O, около которой вращается отрезок, называется центром этого круга. Если какую-либо точку круга (окружности) соединить с центром прямолинейным отрезком, то этот отрезок всегда равен тому, вращением которого образован круг. Называют радиусом круга отрезок, соединяющий точку круга с его центром. Ясно, что все радиусы круга равны между собою. На практике для черчения круга употребляют циркуль. Мы принимаем: на плоскости можно построить круг, центр и радиус которого даны. (Построение круга циркулем ясно указывает нам, что круг образуется вращением того отрезка, который мы можем мысленно вообразить между концами ножек циркуля, около одного из концов этого отрезка.)

Если взять точку на площади круга или внутри круга, то отрезок, соединяющий эту точку с центром, меньше радиуса; если точка расположена где-либо на остальной части плоскости, или, другими словами, вне круга, то отрезок, соединяющий эту точку с центром, больше радиуса круга.

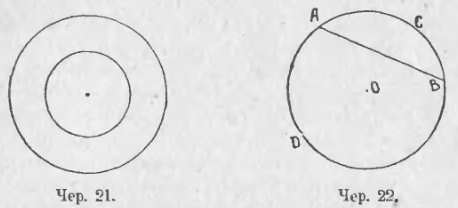
Если построим два круга (черт. 21), имеющие общий центр, но различные радиусы, то один из них, у которого радиус меньше, расположится внутри другого, – такие два круга называются концентрическими. Если построить два круга одинаковыми радиусами, то ясно, что эти круги должны совпасть, если привести в совпадение их центры; говорят, что круги с одинаковыми радиусами равны между собою.

21. Каждая точка окружности делит ее на 2 части; напр., точки A и B (чер. 22) делят окружность на части ACB и ADB. Каждая из этих частей называется дугою и обозначается знаком ◡. Итак, на чертеже имеем две дуги: ◡ACB и ADB. Прямолинейный отрезок, соединяющий концы дуги, называется хордою, стягивающей эту дугу. Хорда AB стягивает ◡ACB и стягивает ◡ADB. Наоборот, ◡ACB (или ◡ADB) стягивается хордою AB.

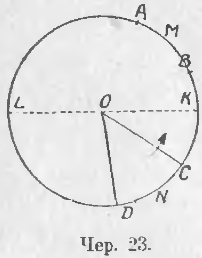
Дуги одного круга можно сравнивать между собою, т. е. узнавать, равны ли они, или одна из них больше другой. Пусть, напр., требуется сравнить ◡AMB и ◡CND (чер. 23); для этого надо наложить ◡CND на ◡AMB. Чтобы удобнее представить процесс наложения, построим радиусы OC и OD и станем вращать фигуру OCND около центра по направлению стрелки до тех пор, пока точка C не придет в точку A: тогда ◡CND пойдет по ◡AMB (это видно из самого образования круга – п. 20). Если точка D совпадет с точкою B, то дуги совпали, и мы признаем их равными: если точка D расположится где-либо внутри ◡AMB, то ◡CND < ◡AMB; если точка D расположится вне ◡AMB, то ◡CND > ◡AMB. Так же легко установить, что можно находить сумму и разность дуг.

Мы уже знаем, что всякая пара точек делит окружность на 2 дуги, напр., на чер. 22 имеем ◡ACB и ◡ADB. Иногда дугу называют двумя буквами ◡AB, и тогда под этим обозначением понимают меньшую из двух дуг, разделяемых точками A и B.

22. Построим какую-либо прямую KL (чер. 23), проходящую через центр нашего круга. Отрезок (напр., OC), вращением которого образован круг, приходит два раза во время вращения, и только два раза, в совпадение с этою прямою: один раз, когда он займет положение OK, и другой раз в положение OL. Поэтому прямая KL имеет с кругом две общих точки K и L. Поэтому:

Всякая прямая, проходящая через центр круга, имеет с ним две, и только две, общих точки.

Отрезок KL, соединяющий эти две общих точки, называется диаметром круга. Ясно, что диаметр равен двум радиусам (напр., LK = LO + OK).

23. Возьмем на круге две дуги: ◡AB и ◡CD (чер. 24) и соединим концы их с центром O; тогда при центре получим углы: ∠AOB и ∠COD. Эти углы называются центральными. Говорят: центральный угол AOB соответствует дуге AB и, наоборот, ◡AB соответствует центральному ∠AOB. Иногда говорят: центральный ∠AOB опирается на ◡AB. Выполним ряд сравнений:

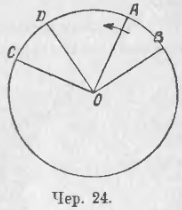
1) Сравнить ◡AB и ◡CD, если ∠AOB = ∠COD.

Вращая фигуру AOB по стрелке до тех пор, пока радиус OA не пойдет по OC, найдем, что вследствие данного равенства углов радиус OB должен пойти по OD, и, следов., ◡AB совместится с ◡CD. Следов., ◡AB = ◡CD.

2) Сравнить ◡AB и ◡CD, если ∠AOB > ∠COD.

Поступая так же, как выше, сообразим, что здесь радиус OB должен пойти вне угла COD, и точка B упадет где-либо на окружности за точкою D; следовательно, здесь ◡AB > ◡CD.

3) Сравнить ∠AOB и ∠COD, если ◡AB = ◡CD.

Так как дуги равны, то, поступая согласно п. 21, можно достигнуть того, чтобы их концы совместились, и тогда радиусы OA и OB должны совместиться соответственно с OC и OD. Следов., ∠AOB = ∠COD.

4) Сравнить ∠AOB и ∠COD, если ◡AB > ◡CD.

Поступая так же, как выше, найдем, что здесь точка A совпадет с C, а точка B попадет куда-либо на окружности за точку D, и, следов., радиус OA совместится с OC, но радиус OB пойдет вне угла COD. Следов., ∠AOB > ∠COD. Итак:

Равным центральным углам соответствуют равные дуги и хорды, большему центральному углу соответствует большая дуга; обратно, равным дугам соответствуют равные центральные углы, большей дуге соответствует больший центральный угол. Также: если 2 хорды равны, то равны и стягиваемые ими дуги и соответствующие центральные углы.

24. Если мы перегнем плоскость, на которой расположена окружность (см. напр., чер. 23), по диаметру LK, то одна часть этой окружности должна при этом перегибании совместиться с другою в силу того, что все радиусы круга равны между собой, а центр при перегибании остался на месте. Это свойство окружности выражают словами:

Диаметр делит окружность пополам,

или

Окружность симметрична относительно диаметра,

или

Диаметр есть ось симметрии окружности.

Вообще, если при перегибании фигуры по какой-либо прямой одна ее часть совмещается с другою, то говорят, что эта фигура симметрична относительно прямой перегиба, или, что прямая, по которой перегибалась фигура, есть ось симметрии этой фигуры.

25. Пусть имеем две окружности с разными центрами. Если можно сообразить, что одна точка второй окружности лежит внутри первой и другая точка второй окружности вне первой, то нашему представлению ясно, что такие две окружности должны иметь общую точку – должны пересекаться. Ясно это из того, что окружность есть непрерывная линия, ограничивающая определенную площадь.

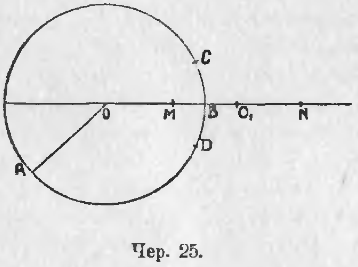
Пусть, напр., имеем окружность O (чер. 25) (окружность часто называют одною буквою по имени ее центра), пусть центр другой окружности есть точка O₁. Соединив точки O и O₁ прямою линиею, получим прямую OO₁, называемую линиею центров этих двух кругов. Эта прямая должна иметь (п. 22) со второю (не нарисованною) окружностью две общих точки по разные стороны центра, напр., M и N, и тогда O₁M и O₁N суть радиусы этой окружности, и, следов., O₁M = O₁N, а MN есть диаметр этой окружности. Допустим, что точка M лежит внутри круга O и точка N вне круга O. Тогда ясно, что окружность O₁, переходя из точки M в точку N, должна где-либо встретить окружность O – должна ее пересечь, и эта точка пересечения есть общая точка обеих окружностей: она принадлежит и окружности O и окружности O₁.

Мы можем найти условия, когда две окружности непременно должны пересечься. Обозначим радиус OA первой окружности для краткости одною буквою a, т. е. пусть OA = a и, следов., также OB = a; радиус второй окружности обозначим b, – следов., O₁M = b и O₁N = b; наконец, обозначим отрезок, соединяющий центры наших кругов, буквою c, т. е. OO₁ = c. Тогда OM = OO₁ – O₁M и ON = OO₁ + O₁N или, пользуясь сделанными обозначениями, найдем

OM = c – b и ON = с + b.

Для того, чтобы точка M лежала внутри первой окружности, необходимо и достаточно, чтобы отрезок OM был меньше радиуса круга O, т. е.

a – b < a,

а чтобы точка N лежала вне первой окружности, необходимо и достаточно, чтобы отрезок ON был больше радиуса круга O, т. е.

c + b > a.

Итак, если выполнены два только что найденных неравенства, то ваши две окружности непременно пересекаются, т. е.:

Если 1) разность между отрезком, соединяющим центры двух кругов, и радиусом одного круга меньше радиуса другого круга и 2) сумма отрезка, соединяющего центры двух кругов, и одного радиуса больше радиуса другого круга, то эти два круга пересекаются.

26. Изучая дальше вопрос о пересечении двух окружностей, мы прежде всего сообразим, что точка пересечения не может лежать на прямой OO₁ (чер. 25), так как на этой прямой, проходящей через центр O₁, у нас имеются 2 точки M и N, второй окружности (п. 22); следов., точка пересечения лежит где-либо вне линии центров. Пусть, напр., эта точка есть точка C. Так как линия центров OO₁, если ее продолжить, явится диаметром, как первого, так и второго круга, то вся наша фигура, состоящая из совокупности обоих кругов, симметрична относительно линии центров OO₁. Поэтому все, что имеет место по одну сторону оси симметрии OO₁, должно иметь место и по другую ее сторону, т. е. и по другую сторону линии центров должна быть точка пересечения наших окружностей, напр., точка D.

Итак, если выполнены условия предыдущего п., при наличности которых наши окружности пересекаются, то непременно должно быть две общих точки у этих окружностей, расположенные симметрично по разные стороны их линии центров.

27. Задача. Найти точку, чтобы отрезки, соединяющие ее с двумя данными точками, были равны двум данным отрезкам.

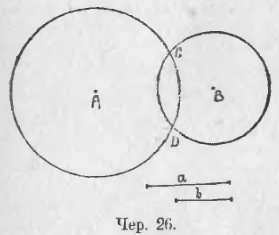
Пусть даны точки A и B (чер. 26) и требуется найти такую точку, чтобы отрезок, соединяющий ее с точкой A, равнялся данному отрезку a и отрезок, соединяющий ее с точкою B, равнялся данному отрезку b.

Для решения этой задачи строим окружность с центром A радиусом = a (если любую точку этой окружности соединить с ее центом A, то полученный отрезок должен быть = a) и из центра B окружности радиусом = b (если соединить любую точку этой окружности с ее центром B, то получим отрезок = b). Если эти окружности пересекутся, то точки пересечения будут искомыми точками.

Назовем отрезок AB через c. Мы знаем, если

c – b < a и c + b > a,

то наши окружности пересекутся в двух точках (пп. 25 и 26), например, в C и D, и тогда мы нашли два решения нашей задачи:

Точки C и D суть искомые.

Если же условия c – b < a и c + b > a не будут выполнены, то задача не имеет решения, – найти такой точки невозможно.

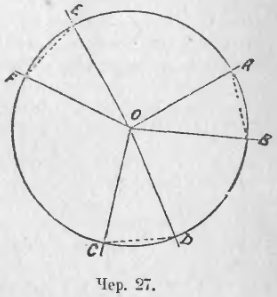
28. Построение угла, равного данному. Из свойств дуг, хорд и центральных углов (п. 23) мы приходим к заключению о возможности строить равные углы. Если имеется круг O (чер. 27) и какой-либо центральный угол AOB, то он вырезает из круга дугу AB, которая стягивается хордою AB. Взяв циркулем эту хорду (она на чертеже изображена пунктиром), перенесем ее в какое-либо иное положение на том же круге, напр., в положение CD (след., хорда CD = хорде AB) или в положение EF (хорда EF = хорде AB); тогда, соединив лучами центр O с концами этих хорд, получим ∠COD = ∠AOB = ∠EOF.

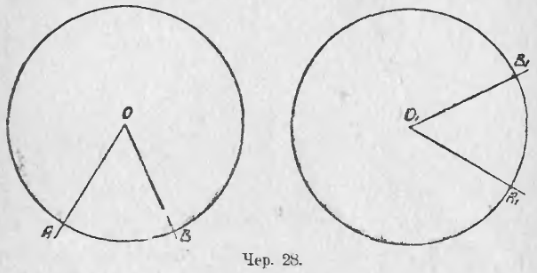
Итак, мы можем теперь построить сколь угодно углов, равных данному, при одной и той же вершине. Попытаемся теперь построить угол, равный данному, при иной вершине. Пусть имеем круг O (чер. 28) и в нем центральный ∠AOB. Построим другой круг O₁ тем же радиусом – круги O и O₁ (п. 20) равны между собою. Затем, взяв циркулем хорду AB, перенесем ее, напр., в положение A₁B₁, на круг O₁ (хорда A₁B₁ = хорде AB – на чертеже эти хорды не изображены, так как их легко вообразить). Тогда, построив лучи O₁A₁ и O₁B₁, получим ∠A₁O₁B₁ = ∠AOB.

Пусть теперь дан ∠1 (чер. 29) при вершине A. Пристроим к нему круг так, чтобы ∠1 вышел центральным; для этого, принимая точку A за центр, опишем произвольным радиусом или полный круг, или, что проще, только дугу круга так, чтобы определились точки E и F, где стороны ∠1 пересекаются с кругом. Тогда определится и хорда EF, соответствующая ∠1-му. Затем, принимая любую точку B за центр, построим таким же радиусом (BE' = AE) дугу и на ней циркулем отметим концы E' и F' хорды E'F', равной хорде EF. Тогда ∠E'B'F' = ∠EAF или ∠2 = ∠1.

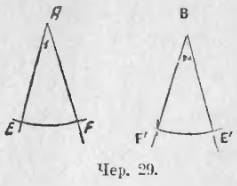
Теперь мы можем решить задачу:

Построить при данной точке угол, равный данному, так, чтобы одна его сторона шла по данному лучу.

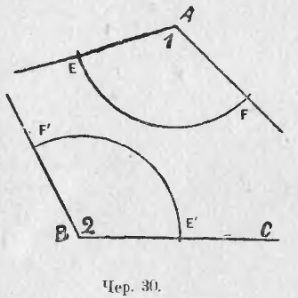
Пусть дан ∠1 с вершиной A (чер. 30) и даны еще точка B и луч BC. Требуется построить угол, равный ∠1, так, чтобы его вершина была в точке B и одна сторона шла по лучу BC.

Опять пристраиваем к ∠1 дугу, принимая т. A за центр (радиус произволен), – тогда определится хорда EF, соответствующая этому углу. Тем же радиусом строим дугу, принимая точку B за центр, причем определится точка E', где эта дуга пересекается с лучом BC. Берем затем хорду EF и этим радиусом, принимая т. E' за центр, строим дугу, пересекающуюся с первой дугой (центр которой в B) в точке F'. Тогда хорда E'F' = хорде EF и, следов., ∠F'BE' = ∠FAE или ∠2 = ∠1.

Упражнения. 1. Даны ∠1 и ∠2; построить сумму и разность этих углов.

2. Построить сумму трех данных углов.