Площадь. Величина поверхности называется площадью.
В начальной геометрии рассматривают площади плоских фигур, ограниченных прямыми линиями или дугами круга.
Совокупность отрезков, ограничивающих площадь, называют ее периметром или обводом. Площади обозначают, называя отрезки ее периметра.
Так площадь на чертеже 205 выговаривают словесно: площадь ABC.
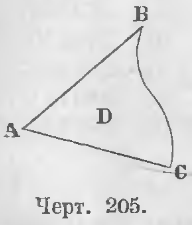
Иногда площадь обозначают одной буквой, которую помещают внутри площади. Так, площадь ABC выговаривают также словесно: площадь D.
Измерить площадь значит найти вывод, получаемый из сравнения ее с другой площадью, принимаемой за единицу площадей.
Единица площадей. За единицу площади принимают площадь квадрата, сторона которого равна единице. Эта площадь называется квадратной единицей.
Площадь квадрата, у которого одна сторона равна аршину, вершку, метру называют квадратным аршином, квадратным вершком, квадратным метром.
Измерить площадь значит найти ее отношение к квадратной единице.
Две плоские фигуры, совпадающие при наложении во всех своих точках, называются равными. Две фигуры, имеющие в своих площадях одинаковое число квадратных единиц, называются равновеликими.
В прямоугольнике одну сторону называют основанием, а другую перпендикулярную к ней высотой.
Так, в прямоугольнике ABCD (черт. 206) сторону AB можно принять за основание, тогда сторона AD будет высотой.
Если за основание примем сторону AD, то сторона AB будет высотой.
Сравнение площадей прямоугольников
Теорема 136. Два прямоугольника, имеющие одинаковые основания и высоты, равны.
Справедливость этой теоремы доказывается простым наложением.
В основе теории площадей плоских прямолинейных фигур лежит следующая теорема.
Теорема 137. Площади прямоугольников, имеющих одинаковые основания, относятся как высоты.
Даны два прямоугольника ABCD и ABFE с одинаковыми основаниями (черт. 206) и разными высотами AD и AE.
Требуется доказать, что ABCD/ABFE = AD/AE.
Доказательство. Здесь могут встретиться два случая: 1) когда высоты соизмеримы и 2) когда они несоизмеримы.
Первый случай. Высоты прямоугольников соизмеримы.
В этом случае они имеют общую меру. Предположим, что их общая мера AG укладывается m раз в большей и n раз в меньшей высоте AE, так что
AD/AE = m/n
Здесь m и n целые числа.
Проведя через точки деления отрезки, параллельные основанию, мы разделим прямоугольник ABCD на m, а прямоугольник ABFE на n равных прямоугольников, так что
ABCD/ABFE = m/n
откуда
ABCD/ABFE = AD/AE.
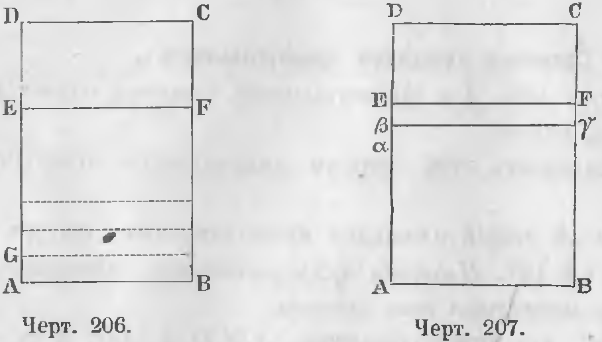
Второй случай. Высоты прямоугольников несоизмеримы.
В этом случае могут существовать следующие три предположения (черт. 207).
ABCD/ABFE > AD/AE, ABCD/ABFE < AD/AE, ABCD/ABFE = AD/AE.
Докажем, что первые два предположения не имеют места.
Действительно, если
ABCD/ABFE > AD/AE
то вторая дробь меньше первой, и следовательно знаменатель второй дроби надо уменьшить для того, чтобы она сравнялась с первой.
Выберем точку α такую, чтобы имело место равенство:
ABCD/ABFE = AD/Aα (a)
Разделим отрезок AD на столько равных частей, чтобы каждая часть была меньше αE, тогда одна из точек деления упадет в точку β, находящуюся между α и E.
Проведя отрезок βγ параллельно основанию, мы будем иметь прямоугольник AβγB, высота которого Aβ соизмерима с высотой AD, следовательно,
ABCD/Abγβ = AD/Aβ (b)
Разделив равенства (a) и (b), имеем равенство:
ABγβ/ABFE = Aβ/Aα
первая часть которого меньше 1, а вторая больше 1.
Такое равенство несообразно, следовательно, предположение, что ABCD/ABFE > AD/AE ведет к нелепости и не может быть допущено.
Точно также легко доказать, что неравенство
ABCD/ABFE < AD/AE
приводит к нелепости, следовательно, имеет место равенство:
ABCD/ABFE = AD/AE
Так как за основание можно принять любую сторону прямоугольника, то отсюда вытекает как простое следствие следующая теорема.
Теорема 138. Площади прямоугольников, имеющие одинаковые высоты, относятся как основания.
Теорема 139. Площади прямоугольников, имеющих разные основания и высоты, относятся как соответствующие произведения их оснований на высоты.
Дано. Два прямоугольника ABCD и abcd (черт. 208) имеют разные основания и высоты.
Требуется доказать, что
ABCD/abcd = (AD · AB) / (ad · ab).
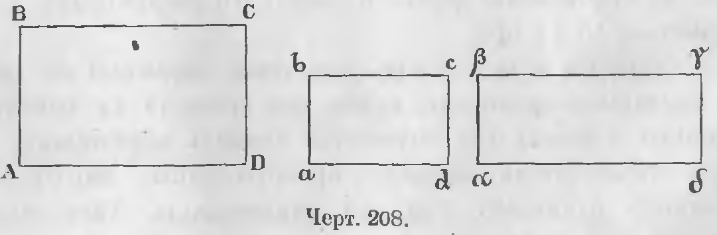
Доказательство. Начертим такой прямоугольник αβγδ, который имел бы основание одинаковое с первым и высоту одинаковую со вторым прямоугольником, т. е.
αδ = AD и αβ = ab.
На основании теорем 137 и 138 имеют место два равенства:
ABCD/ αβγδ = AB/αβ и αβγδ/abcd = αδ/ad.
Перемножив эти две пропорции, получим:
(ABCD · αβγδ) / (αβγδ · abcd) = (AB · αδ) / (αβ · ad)
Заменив αδ и αβ равными им величинами AD и ab, получим:
ABCD/abcd = (AD · AB) / (ad · ab).
Теорема 140. Площадь прямоугольника равна произведению основания на высоту.
Дано. Полагая, что за единицу площадей выбрана площадь квадрата, у которого сторона равна единице, мы в равенстве
ABCD/abcd = (AD · AB) / (ad · ab)
должны принять ab = ad = 1, abcd = 1, следовательно,
ABCD = AB · AD.
В этом случае величины AB и AD выражают число линейных единиц, а само произведение AB · AD выражает число квадратных единиц, т. е. число квадратов, сторона которых равна единице.
Если одна сторона прямоугольника равна 5 аршинам, а другая 3 арш., то его площадь равна 3 · 5 или 15 квадратным аршинам = 15 кв. арш.
Если основание и высота прямоугольника выражены в различных линейных единицах, нужно их привести к одному наименованию, а потом для вычисления площади перемножить полученные числа, тогда площадь прямоугольника, выразится в квадратных единицах того же наименования. Так, площадь прямоугольника, имеющего своим основанием 2 сажени и выстой 3 ф. вычисляется следующим образом:
основание = 14 фут.
высота = 3 фут.
площадь = 14 · 3 кв. ф. = 42 кв. фут.
Площадь квадрата равна квадрату его стороны.
Обозначив длину стороны квадрата через a и заметив, что его высота равна тоже a, мы имеем, что площадь квадрата равна a2.
В параллелограмме ABCD принимают за основание одну из сторон AD, тогда высота есть расстояние основания от другой ему параллельной стороны, считаемое по перпендикуляру к основанию. В параллелограмме ABCD основанием будет сторона AD (черт. 209), а высотой длина перпендикуляра BE.
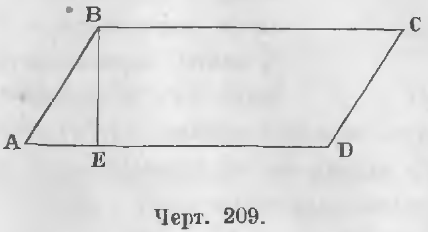
Теорема 141. Площадь параллелограмма равна площади прямоугольника того же основания и той же высоты.
Доказательство. Опустив из точек A и D (черт. 210) перпендикуляры Aa и Db, мы видим, что ΔAaB = ΔDbC, ибо треугольники прямоугольные и AB = CD как стороны параллелограмма. Aa = Db как расстояния сторон параллелограмма.

Приложив к равенству
ΔAaB = ΔDbC
площадь фигуры ABbD, имеем:
AaB + ABbD = bCD + ABbD или
площадь прямоугольника AabD равна площади параллелограмма ABCD.
Отсюда вытекает заключение: Площадь параллелограмма равна произведению его основания на высоту, или
ABCD = AD · Aa.
Теорема 142. Площадь треугольника равна половине произведения основания на высоту.
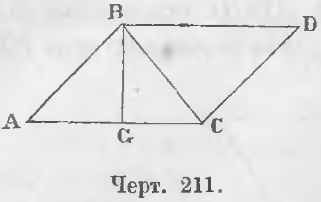
Доказательство. Всякий треугольник равен половине параллелограмма того же основания и той же высоты. Действительно, проведя через точку B треугольника ABC (черт. 211) прямую параллельную AC и через точку C прямую параллельную AB и продолжив их до взаимного пересечения в точке D, получим параллелограмм ABCD, у которого основание AC и высота BG одинаковы с основанием и высотой треугольника ABC. В этом параллелограмме ΔABC = ΔBDC, ибо BC сторона общая, AB = CD, AC = BD как противоположные стороны параллелограмма. Следовательно,
ABDC = ABC + BDC = 2ABC
откуда
ABC = ½ ABDC
Обозначив основание треугольника AC через b, а высоту BG через h, имеем:
ABC = (bh)/2 = ½ bh
Отношение площадей треугольников. 1. Треугольники, имеющие одинаковые основания, относятся как высоты.
Пусть b и h означают основание и высоту треугольника T, а b и h' основание и высоту треугольника T'.
Площадь первого треугольника T = ½ bh
Площадь второго T' = ½ bh'
Следовательно,
T/T' = (½ bh) / (½ bh') = h/h'
2. Площади треугольников, имеющих одинаковые высоты, относятся как основания.
Пусть b и h основание и высота треугольника T, b' и h основание и высота треугольника T', откуда
T/T' = (½ bh) / (½ b'h) = b/b'
Теорема 143. Площадь трапеции равна произведению полусуммы параллельных сторон на высоту.
Дана трапеция ABCD (черт. 212).
Требуется доказать, что ABCD = ½ (BC + AD) · BE.
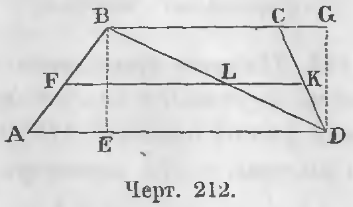
Доказательство. В данной трапеции ABCD соединим точки B и D.
Трапеция разобьется на два треугольника ABD и BCD.
Мы будем вообще площадь ABD просто называть ABD. Из чертежа видно, что
ABCD = ABD + BCD.
Площади треугольников ABD и BCD равны половине произведения основания на высоту, следовательно,
ABD = ½ AD · BE
BCD = ½ BC · DG
Так как BE = DG, то, сложив эти равенства, имеем:
ABCD = ½ AD · BE + ½ BC · BE = ½ BE (AD + BC) = BE · ((AD + BC)/2)
Если через точку F середину стороны AB проведем прямую, параллельную AD, то найдем, что
FK = FL + LK, где
FL = ½ AD
LK = ½ BC
следовательно,
½ (AD + BC) = FL + LK = FK
и площадь
ABCD = BE · FK
Площадь трапеции равна высоте, умноженной на отрезок, соединяющий середины непараллельных сторон.
Теорема 144. Площадь правильного многоугольника равна половине произведения периметра на апофему.
Дан правильный многоугольник ABCDEF, O его центр (черт. 213), OG его апофема, p его периметр.
Требуется доказать, что ABCDEF = ½ p · OG.
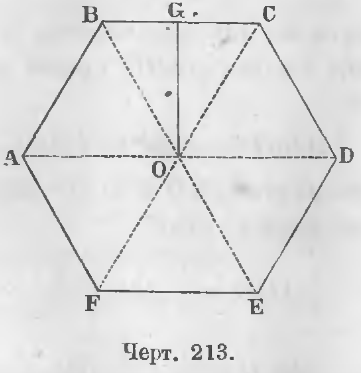
Доказательство. Если соединим центр O с вершинами многоугольника, то он разобьется на равные треугольники AOB, BOC, COD и т. д.
Площадь ABCDEF = n · BOC
BOC = ½ BC · OG, следовательно, ABCDEF = ½ n · BC · OG
Так как p = nBC, то
ABCDEF = ½ p · OG (ЧТД).
Теорема 145. Площадь треугольника выражается по трем его сторонам. Она равна корню квадратному из произведения полупериметра на полупериметр без первой, на полупериметр без второй, на полупериметр без третьей стороны.
Дано. В треугольнике ABC даны три стороны (черт 214)
BC = a, AC = b, AB = c
Обозначим периметр его через 2p, т. е. 2p = a + b + c.
Требуется доказать, что площадь ABC = 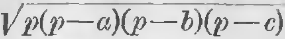
Замечание. Обычно в треугольнике длину сторон обозначают малыми буквами тех углов, против которых лежат данные стороны.
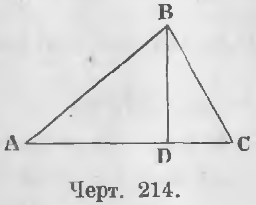
Доказательство. Опустив перпендикуляр BD, получим:
ABC = ½ AC · BD = ½ b · BD
Из прямоугольного треугольника ABD имеем:
BD2 = AB2 - AD2 = c2 - AD2
Сторона BC как сторона, лежащая против острого угла, выражается равенством:
BC2 = AB2 + AC2 - 2AC · AD
или
a2 = c2 + b2 - 2b · AD
откуда

Теорема 146. Всякий многоугольник можно превратить в равновеликий треугольник.
Чтобы превратить пятиугольник ABCDE (черт. 215) в равновеликий треугольник, мы превратим его сначала в равновеликий четырехугольник. Для этого проведем диагональ CE и продолжим сторону AE.
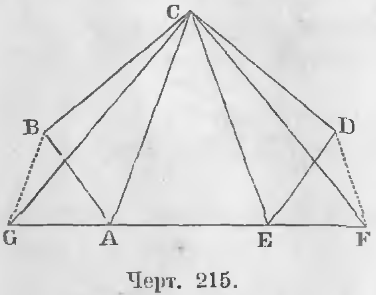
Через точку D проведем прямую DF параллельную CE до пересечения ее в точке F с прямой CE и соединим C с F.
Два треугольника CDE и CFE равновелики, ибо они имеют общее основание CE и равные высоты, так как вершины их D и F лежат на одной и той же прямой DF параллельной основанию CE, следовательно, площадь CDE равна площади CEF.
Добавив к этому равенству по равной площади BCEF, получим, что площадь пятиугольника ABCDE равна площади четырехугольника ABCF.
Подобным построением каждый многоугольник превращается в многоугольник, имеющий число сторон на единицу меньше.
Превратим теперь четырехугольник ABCF в равновеликий треугольник. Для этого проведем диагональ AC, из точки B прямую BG параллельную AC до пересечения ее с прямой AF в точке G и соединим G с C. Два треугольника ABC и AGC равновелики: площадь ABC равна площади AGC.
Прибавив по ACF, получим: площадь четырехугольника ABCF равна площади треугольника GCF.
Подобным построением каждый многоугольник превращается в равновеликий с ним треугольник.
Площадь неправильного многоугольника. Чтобы определить площадь неправильного многоугольника, нужно или разбить его на треугольники или превратить в равновеликий треугольник, а затем определить площадь этого треугольника.
Теорема 147. Квадрат, построенный на гипотенузе, равен сумме квадратов, построенных на катетах.
Дан прямоугольный треугольник ABC (черт. 216) и три квадрата, построенные на его сторонах: квадрат ACDE, построенный на гипотенузе AC и квадраты BCLK, ABGF, построенные на катетах BC и AB.
Требуется доказать, что
ACDE = BCLK + ABGF
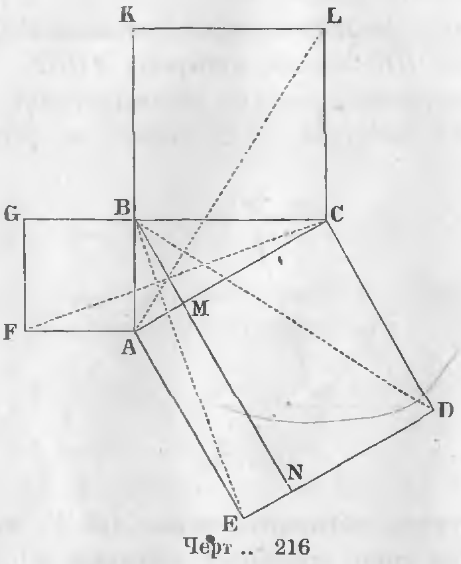
Доказательство. Из вершины B прямого угла опустим перпендикуляр BM на гипотенузу AC и продолжим его до пересечения со стороной ED в точке N.
Проведем прямые FC и BE.
Треугольник AFC имеет одинаковые основание и высоту с квадратом ABGF, следовательно,
AFC = ½ ABGF
Треугольник ABE имеем одинаковые основание AE и высоту с прямоугольником AMNE, следовательно,
ABE = ½ AMNE
У двух треугольников AFC и ABE
AB = AF как стороны квадрата AG
AE = AC как стороны квадрата AD
∠FAC = ∠BAE, ибо каждый угол состоит из прямых углов FAB и CAE, к которым приложен угол BAC, составляющий их общую часть. Следовательно, ΔAFC = ΔABE и откуда ½ ABGF = ½ AMNE и
ABGF = AMNE (a)
Точно также легко доказать, что
BCLK = CDNM
Проведя прямые AL и BD, получим два треугольника ALC и BCD.
Треугольник ALC имеет основание и высоту одинаковые с квадратом BCLK, следовательно,
ALC = ½ BCLK.
Треугольник BCD имеет основание CD и высоту одинаковые с прямоугольником CDMN, следовательно,
BCD = ½ CDNM
У двух треугольников ALC и BCD
CL = BC как стороны квадрата CK
AC = CD как стороны квадрата AD
∠ACL = ∠BCD
Следовательно, ΔALC = ΔBCD. Откуда ½ BCLK = ½ CDNM и
BCLK = CDNM (b)
Сложив равенства (a) и (b), имеем:
ABGF + BCLK = AMNE + CDNM = ACDE, т. е.
ACDE = ABGF + BCLK (ЧТД).
Это предположение называется Пифагоровой теоремой.
Теорема 148. Площади двух треугольников, имеющих по равному углу, относятся как произведения сторон, заключающих равные углы.
Даны два треугольника ABC и abc (черт. 217), у которых ∠A = ∠a.
Требуется доказать, что
ABC/abc = (AB · AC) / (ab · ac).
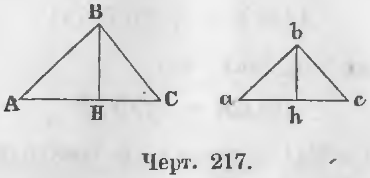
Доказательство. Принимая AC и ac за основания двух треугольников, проведем высоты BH и bh. Площади треугольников относятся как соответствующие произведения их оснований на высоты:
ABC/abc = (AC · BH) / (ac · bh) (a)
Два треугольника ABH и abh подобны, ибо они прямоугольны и ∠A = ∠a по условию, следовательно,
AB/ab = BH/bh
Заменяя в равенстве (a) отношение BH/bh отношением AB/ab, получим равенство:
ABC/abc = (AC · AB) / (ac · ab) (ЧТД).
Теорема 149. Площади подобных треугольников относятся как квадраты соответственных сторон.
Даны два подобных треугольника ABC и abc (черт. 218), следовательно,
∠A = ∠a, ∠B = ∠b, ∠C = ∠c и
AB/ab = AC/ac = BC/bc (a)
Требуется доказать, что ABC/abc = AB2/ab2 = BC2/bc2 = AC2/ac2.
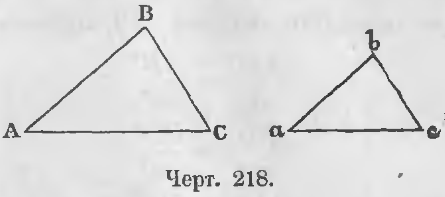
Доказательство. Так как ∠A = ∠a, то на основании предыдущей теоремы
ABC/abc = (AC · AB) / (ac · ab) (b)
Заменяя в равенстве (b) отношение AC/ac отношением AB/ab, по условию (a) получаем:
ABC/abc = AB2/ab2
На основании равенства (a), имеем:
ABC/abc = AB2/ab2 = AC2/ac2 = BC2/bc2 (ЧТД).
Теорема 150. Площади подобных многоугольников относятся как квадраты соответственных сторон.
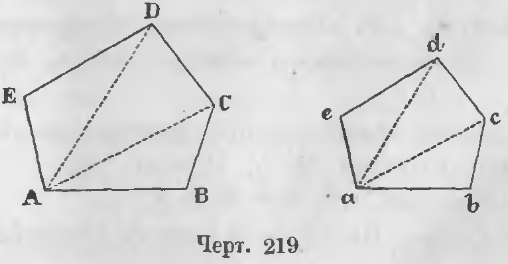
Даны два подобных многоугольника ABCDE и abcde (черт. 219).
Требуется доказать, что
ABCDE/abcde = AB2/ab2 = BC2/bc2 = и т. д.
Доказательство. Из того, что многоугольники ABCDE и abcde подобны, следуют отношения:
AB/ab = BC/bc = CD/cd = DE/de = AE/ae (1)
Многоугольники разбиваются диагоналями на треугольники подобные, следовательно, на основании теоремы 149, имеем пропорции:
ABC/abc = AB2/ab2
ACD/acd = CD2/cd2
ADE/ade = DE2/de2
На основании соотношений (1) имеем равные отношения:
AB2/ab2 = BC2/bc2 = CD2/cd2 = DE2/de2 = AE2/ae2
следовательно,
ABC/abc = ACD/acd = ADE/ade = AB2/ab2
откуда по свойству пропорций имеем:
(ABC + ACD + ADE) / (abc + acd + ade) = ABCDE / abcde = AB2/ab2 (ЧТД).
Так как одноименные правильные многоугольники подобны, то площади одноименных правильных многоугольников относятся как квадраты их сторон.
Теорема 151. Многоугольник, построенный на гипотенузе, равен сумме подобных многоугольников, построенных на катетах.
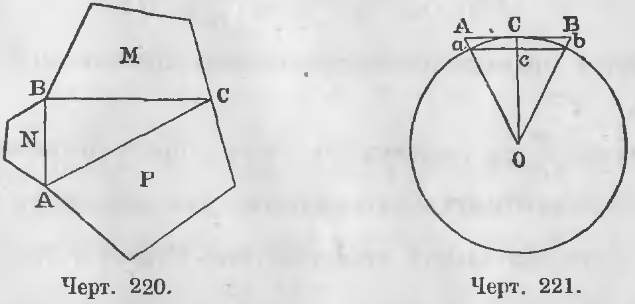
Дано. На сторонах прямоугольного треугольника ABC построены подобные многоугольники M, N, P (черт. 220).
Требуется доказать, что P = M + N.
Доказательство. На основании теоремы 150 имеем отношения:
M/P = BC2/AC2
N/P = AB2/AC2
откуда, сложив эти равенства, имеем:
(M + N)/P = (BC2 + AB2)/AC2
По свойству прямоугольных треугольников имеем:
AC2 = BC2 + AB2
следовательно,
(M + N)/P = 1, откуда M + N = P (ЧТД).
Теорема 152. С увеличением числа сторон площади правильных вписанных и описанных многоугольников приближаются к одному и тому же пределу.
Даны ab и AB (черт. 221) стороны одноименных правильных многоугольников вписанного и описанного.
Требуется доказать, что разность между их площадями может быть сделана меньше всякой данной величины.
Доказательство. Обозначив через Sn и sn площади, Pn и pn периметры, An и an стороны правильных одноименных многоугольников описанного и вписанного и через r радиус круга, мы по теореме 144 имеем:
Sn = ½ Pn · OC = ½ Pnr
sn = ½ pn · Oc
Так как
Pn/pn = OC/Oc = r/Oc, Pn = pn (r/Oc)
следовательно,
Sn = ½ pn · (r2/Oc), sn = ½ pn · Oc
откуда
Sn - sn = ½ pn · ((r2 - Oc2)/Oc).
В этом равенстве
r2 - Oc2 = aO2 - Oc2 = ac2
следовательно,
Sn - sn = ½ pn · (ac2/Oc2) (1)
Периметр правильного вписанного многоугольника меньше окружности pn < 2πr.
Отношение ac/Oc с увеличением числа сторон правильного вписанного многоугольника уменьшается. Для вписанного квадрата ac/Oc = 1. Если правильный многоугольник имеет больше 4-х сторон, то
ac/Oc < 1.
Следовательно, для n > 4
pn (ac/Oc) < 2πr
Заменив в равенстве (1) pn (ac/Oc) через 2πr, получим неравенство:
Sn - sn < πr · ac
Так как ac = ½ an, то
Sn - sn < ½ πr · an (2)
В этом неравенстве величины π и r постоянные, а сторона правильного вписанного многоугольника может быть сделана меньше всякой данной величины, следовательно, разность Sn - sn может быть сделана меньше всякой данной величины. Откуда
lim (Sn - sn) = 0 и lim Sn = lim sn (ЧТД).
Теорема 153. Круг есть предел площадей правильного вписанного и описанных многоугольников.
Доказательство. Обозначив площадь круга через C, через Sn и sn площади, An и an стороны правильных многоугольников описанного и вписанного, имеющего больше четырех сторон, мы по предыдущему имеем:
Sn - sn < ½ πr · an
Так как
Sn > C, sn < C
то и подавно
C - sn < ½ πr · an
следовательно, разность между площадью круга и площадью правильного вписанного многоугольника может быть с увеличением числа сторон сделана меньше всякой данной величины, поэтому
lim sn = C
а так как lim Sn = lim sn, то и lim Sn = C.
Теорема 154. Площадь круга равна длине окружности, умноженной на половину радиуса.
Доказательство. Обозначим через Pn и Sn периметр и площадь правильного описанного многоугольника, имеющего n сторон, через O длину окружности, C площадь и r радиус круга.
Известно, что
Sn = Pn · ½ r
Так как круг есть предел площадей описанных и вписанных правильных многоугольников, то
Sn = C + α
Pn = O + β
где с увеличением n числа сторон правильного описанного многоугольника величины α и β могут быть сделаны меньше всякой данной величины.
Вставляя вместо Sn и Pn их величины, находим:
C + α = (O + β) ½ r
Откуда на основании теоремы 129 находим выражение площади
C = O · ½ r
Так как O = 2πr, то
C = 2πr · ½ r = πr2
Площадь круга равна отношению окружности к диаметру, умноженному на квадрат радиуса.
Теорема 155. Площадь сектора равна дуге, умноженной на половину радиуса.
Доказательство. Обозначим длину дуги сектора через s и его площадь через c. Площадь круга относится к площади сектора как окружность к дуге сектора
C/c = O/s
откуда
c = sC/O
Так как
C = πr2, O = 2πr, то
C/O = r/2, следовательно,
c = s · (r/2)
Для дуги, имеющей n градусов, имеем:
s = (2πr · n)/360, c = (πr2 · n)/360
Теорема 156. Площади секторов двух кругов с одинаковым числом градусов относятся как квадраты радиусов.
Доказательство. Для двух кругов с радиусами r и r' площади секторов c и c', имеющих n градусов, выражаются формулами:
c = (πr2 · n)/360, c' = (πr'2 · n)/360
откуда
c/c' = r2/r'2
Теорема 157. Круг, построенный на гипотенузе, как на диаметре, равен сумме кругов, построенных на катетах.
Доказательство. Обозначив через a, b длину катетов и через c длину гипотенузы, через A, B, C площади кругов, построенных на них, мы имеем:
A = π(a2/4), B = π(b2/4), C = π(c2/4) (1)
Так как
c2 = a2 + b2
Умножив это равенство на π/4, имеем:
(πc2)/4 = (πa2)/4 + (πb2)/4
На основании равенства (1) получаем:
C = A + B (2)
Тоже заключение имеет место и для полукруга. На этом свойстве основана квадратура суммы двух криволинейных фигур, называемых Гиппократовыми луночками.
Гиппократова луночка есть фигура, ограниченная двумя дугами кругов, обращенными в одну сторону.
Взяв прямоугольный треугольник ABC (черт. 222) и построив полукруги на сторонах AC, AB и BC как на диаметрах, мы имеем равенство, обозначающее, что полукруг, построенный на диаметре AC, равен сумме полукругов, построенных на катетах AB и BC.
AFBGCA = ADBA + BECB
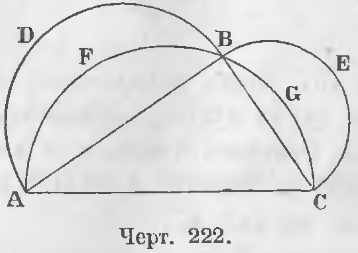
Вычитая из обеих частей сумму сегментов AFBA + BGCB, имеем:
ΔABC = ADBFA + BECGB
т. е. луночка ADBFA + луночка BECGB = ΔABC.
Это есть один из замечательных случаев квадратуры криволинейных фигур.
Задача. Разделить треугольник на три равные части из точки, находящейся на одной из его сторон.
Дана точка D на стороне AC треугольника ABC (черт. 223).
Требуется разделить площадь треугольника ABC прямыми, выходящими из точки B.
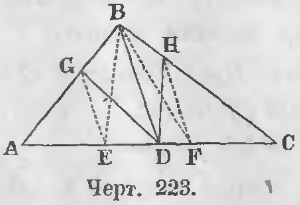
Решение. Положим, что прямые DH и DG действительно делят треугольник на три равные части. Разделим основание AC на три части и точки деления E и F соединим с точкой B. Отрезки BE и BF тоже делят треугольник на три равные части.
Соединим точки H и G с точками E и F.
Так как треугольники BCF и DHG имеют общий угол C, то по теореме 148
BCF/DHC = (BC · CF) / (HC · CD)
Площади BCF и DHC равны, ибо они составляют третью часть площади треугольника ABC, следовательно,
(BC · CF) / (HC · CD) = 1
откуда
BC · CF = HC · CD
или
BC/CD = HC/FC
Из этой пропорции видно, что сторона HF делит стороны треугольника BCD на части пропорциональные, следовательно, отрезок HF параллелен BD.
Точно также нетрудно доказать, что отрезок GE параллелен отрезку BD. Отсюда вытекает следующее построение. Чтобы разделить треугольник на три равные части из точки, находящейся на одной из его сторон, делим эту сторону на три равные части, соединяем данную точку с вершиной и из точек деления проводим прямые ей параллельные. Точки пересечения этих параллельных со сторонами треугольника соединяем с данной точкой. Эти отрезки и будут рассекать треугольник на три равные части.
