Подобные многоугольники. Подобными называются такие одноименные многоугольники, у которых соответственные углы равны и соответственные стороны пропорциональны.

Соответственными сторонами подобных многоугольников называются стороны, соединяющие равные углы.

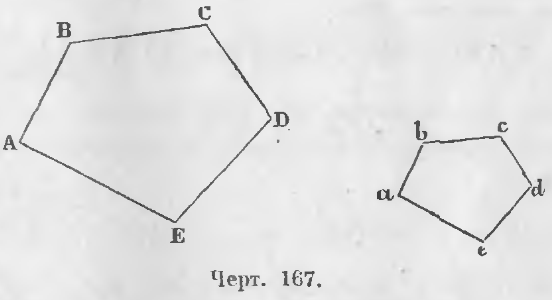
Два многоугольника ABCDE и abcde (черт. 167) подобны, если

∠A = ∠a, ∠B = ∠b, ∠C = ∠c, ∠D = ∠d, ∠E = ∠e и
AB/ab = BC/bc = CD/cd = DE/de = EA/ea

 

Отношение подобия. Отношение двух соответствующих сторон называется отношением подобия.

Теорема 108. Периметры подобных многоугольников относятся как соответственные стороны.

Дано. Обозначим периметры двух подобных многоугольников (черт. 167) через P и p.

P = AB + BC + CD + DE + EA
p = ab + bc + cd + de + ea

Требуется доказать, что P/p = AB/ab.

Доказательство. Из самого определения подобия двух многоугольников ABCDE и abcde (черт. 167) вытекают равенства:

AB/ab = BC/bc = CD/cd = DE/de = EA/ea

На основании той теоремы, что сумма предыдущих относится к сумме последующих как предыдущий член относится к последующему, имеет место равенство:

(AB + BC + CD + DE + EA) / (ab + bc + cd + de + ca) = AB/ab

откуда P/p = AB/ab (ЧТД).

Теорема 109. Подобные многоугольники разбиваются диагоналями на треугольники подобные и одинаково расположенные.

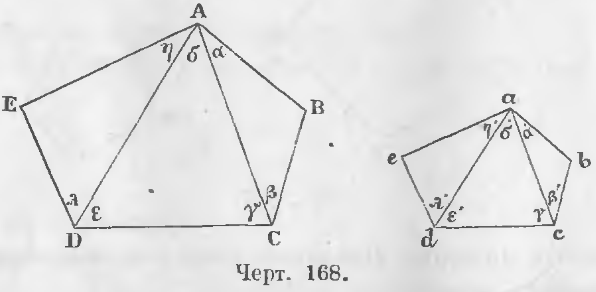
Дано. Разобьем подобные многоугольники ABCDE и abcde диагоналями AC, AD, ac, ad на одинаково расположенные треугольники (черт. 168).

Требуется доказать, что

ABC ~ abc, ACD ~ acd, ADE ~ ade.

Доказательство. Из подобия многоугольников следует, что углы равны и стороны пропорциональны.

∠A = ∠a, ∠B = ∠b, ∠C = ∠c, ∠D = ∠d, ∠E = ∠e и
AB/ab = BC/bc = CD/cd = DE/de = EA/ea

1) Треугольники ABC и abc подобны, ибо

∠B = ∠b и AB/ab = BC/bc

т. е. они имеют по равному углу, заключающемуся между пропорциональными сторонами, следовательно, ∠α = ∠α', ∠β = ∠β' и диагонали пропорциональны сторонам

AB/ab = BC/bc = AC/ac

2) Точно также треугольники ACD и acd подобны, ибо

∠γ = ∠γ' и
AC/ac = CD/cd

следовательно,

∠δ = ∠δ', ∠ε = ∠ε' и
AD/ad = CD/cd

3) Наконец треугольники ADE и ade подобны, ибо

AE/ae = ED/ed и ∠E = ∠e

Из этой теоремы вытекает следствие. В подобных многоугольниках стороны пропорциональны диагоналям.

Теорема 110 (обратная 109). Два многоугольника, состоящие из одинаково расположенных подобных треугольников, подобны.

Дано. Положим, что

∆ABC ~ ∆abc, ∆ACD ~ ∆acd, ∆ADE ~ ∆ade (черт. 168).

Требуется доказать, что многоугольники ABCDE и abcde подобны.

Доказательство. Из подобия треугольников ABC и abc следует, что углы

B = b, α = α', β = β' и
AB/ab = BC/bc = AC/ac (1)

Из подобия треугольников ACD и acd следует, что углы

γ = γ', δ = δ' и
AC/ac = CD/cd = AD/ad (2)

Из подобия треугольников ADE и ade следует, что

η = η', λ = λ', E = e и
AD/ad = AE/ae = DE/de (3)

Из равенства для углов выходит, что

B = b
A = α + δ + η = α' + δ' + η' = a
E = e
D = ε + λ = ε' + λ' = d
C = β + γ = β' + γ' = c

Из сравнения равенств (1), (2) и (3) вытекает, что

AB/ab = BC/bc = CD/cd = DE/de = AE/ae

следовательно многоугольники ABCDE и abcde подобны (ЧТД).