142. В п. 114 мы нашли, что перпендикуляры к сторонам треугольника чрез их середины пересекаются в одной точке, а именно в центре круга, описанного около треугольника.
В п. 126 мы нашли: 1) биссекторы внутренних углов треугольника пересекаются в одной точке, а именно в центре вписанного в этот треугольник круга и 2) биссекторы двух вешних углов треугольника и биссектор одного внутреннего угла пересекаются в одной точке, а именно в центре круга, вне-вписанного в треугольник.

Кроме этих, особых точек треугольника, рассмотрим еще следующие:

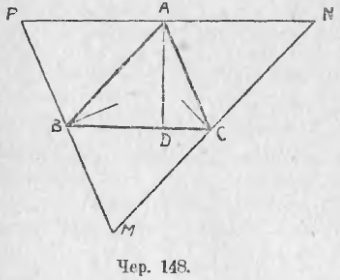
143. В треугольнике ABC (чер. 148) построим его три высоты (на чертеже начерчены лишь части этих высот). Можно увидать, что они все три пересекаются в одной точке (с этим свойством мы уже встречались в п. 71). Для выяснения этого чрез точку A построим прямую PN || BC, чрез B — PM || AC и чрез C — MN || AB. Тогда получим новый треугольник MNP, для которого точки A, B и C служат серединами сторон. В самом деле, ABCN есть параллелограмм, – следовательно, AN = BC; также ACBP есть параллелограмм, – следовательно, AP = BC, откуда вытекает, что AN = AP. Также выясним, что B есть середина PM и C середина MN. Высота AD нашего треугольника перпендикулярна к BC, но PN || BC, следовательно, AD ⊥ PN; также найдем, что и другие высоты нашего треугольника соответственно перпендикулярны к MP и к MN. Мы видим таким образом, что высоты ∆ABC являются перпендикулярами к сторонам ∆MNP чрез их середины, а об них мы уже знаем, что они пересекаются в одной точке, а именно, в центре круга, описанного около ∆MNP.

144. Интересны следующие свойства точки пересечения высот: 1) Пусть имеем ∆ABC (чер. 149) и его высоты пересекаются в точке H. Рассмотрим затем ∆ABH: легко увидать, что его высотами служат прямые AC, BC и CF, которые пересекаются в точке C. Также высоты треугольника AHC пересекаются в точке B и высоты треугольника BHC в точке A.

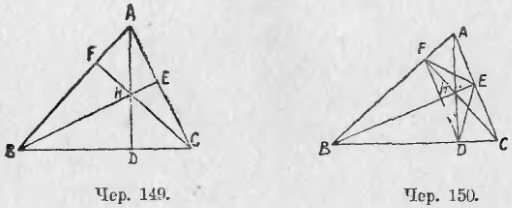
2) Пусть дан ∆ABC, у которого все углы острые (чер. 150), высоты AD, BE и CF пересекаются в точке H. Соединим прямыми точки D, E и F; получим ∆DEF. Около 4-угольника DHEC можно описать круг, так как ∠HDC + ∠HEC = 2d (ибо каждый из этих углов прямой), тогда ∠HDE = ∠HCE, так как эти углы окажутся вписанными в указанный круг, опирающимися на одну и ту же его дугу HE. Также, описав круг около четырехугольника BFHD (∠BFH = d и ∠BDH = d), найдем, что ∠FDH = ∠FBH, как вписанные, опирающиеся на одну и ту же дугу FH. Но ∠HCE = d – ∠A, так как ∆AFC прямоугольный и сумма острых его углов ∠A + ∠FCE = d. Также найдем, что ∠FBH = d – ∠A; поэтому ∠HCE = ∠FBH и, следовательно, ∠HDE = ∠HDF, т. е. AD является биссектором внутреннего угла ∆DFE. Также найдем, что BE и CF суть другие два биссектора. Поэтому точка H является центром круга, вписанного в треугольник DFE.

Если данный треугольник имеет тупой угол, то точка пересечения его высот лежит вне треугольника и является центром вне-вписанного круга в треугольник, вершинами которого служат основания высот. Напр., точка C (чер. 149) — точка высот ∆ABH — служит центром вне-вписанного круга в ∆DEF.

3) Пусть в ∆ABC (чер. 151) имеем AD ⊥ BC, BE ⊥ AC и точка пересечения этих высот H; затем пусть M и N середины сторон BC и AC и MO ⊥ BC, NO ⊥ AC, – тогда O есть центр круга, описанного около ∆ABC. Построив отрезок MN, найдем, что он есть средняя линия ∆ABC и поэтому MN || AB и MN = AB/2. Построим среднюю линию KL треугольника AHB; тогда KL || AB и KL = AB/2. Отсюда заключаем, что KL = MN. Далее найдем, что ∠KLH = ∠MNO, как углы с параллельными сторонами (ON || BE, так как обе эти прямые перпендикулярны к AC) и также, что ∠KHL = ∠MON по той же причине. Отсюда заключаем, что ∆KHL = ∆MON и, следовательно, OM = HK, но HK есть половина отрезка AH (ибо KL средняя линия ∆AHB), который называют иногда верхним отрезком высоты AD. Поэтому имеем OM = ½HA или HA = 2OM. Это свойство можно выразить в такой форме:
Точка высот треугольника отстоит от его вершины вдвое дальше, чем центр описанного круга от противоположной стороны.

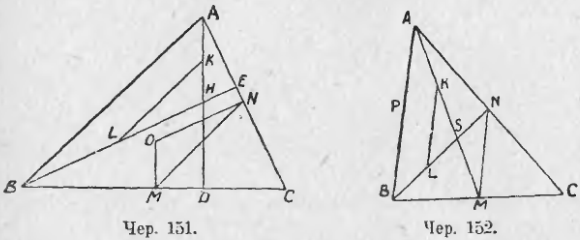
145. Построим теперь две медианы ∆ABC (медианою называется прямая, соединяющая вершину треугольника с серединою противоположной стороны), – пусть они суть AM и BN (чер. 152) и пусть их точка пересечения есть S. Построив отрезок MN – он является среднею линиею ∆ABC, – найдем MN || AB и MN = AB/2. Построим также среднюю линию KL ∆ASB (следовательно, K есть середина AS и L — середина BS); тогда имеем KL || AB и KL = AB/2. Отсюда заключаем, что MN = KL. Нетрудно видеть, что ∆SMN = ∆SKL, так как у них MN = KL, ∠N = ∠L и ∠M = ∠K, как внутренние накрест-лежащие при параллельных. Следовательно, SM = KS, но KS = AK (K середина AS), – следовательно, SM = SK = AK или SM = AM/3, т. е. медиана BN отсекает от медианы AM ее третью часть; также SN = 1/3 BN. Если теперь построить третью медиану CP треугольника ABC, то и она должна отсечь от AM отрезок, равный 1/3 AM, т. е. должна пройти чрез ту же точку S. Итак:

Три медианы треугольника пересекаются в одной точке, причем отрезок каждой медианы от этой точки до стороны треугольника равен 1/3 всей медианы.

Точка пересечения медиан называется центром тяжести этого треугольника.

146. Три точки: центр описанного круга, точка высот (иногда ее называют ортоцентр) и центр тяжести треугольника имеют связь, которую теперь выясним. В ∆ABC (чер. 153) пусть AH есть высота и H точка высот, O — центр описанного круга и OM ⊥ BC (M середина BC). Тогда AM есть медиана треугольника. Соединим O и H — пусть S есть точка пересечения AM и OH — и построим KL, среднюю линию ∆AHS; тогда KL || SH и, следовательно, ∠AKL = ∠AHO = ∠SOM (последнее равенство справедливо потому, что AH || OM). Кроме того, имеем ∠SAH = ∠SMO (как внутренние накрест-лежащие при параллельных AH и OM и секущей AM) и AK = OM, так как AK = ½ AH и OM = ½ AH (п. 144; 3-е свойство). Поэтому ∆AKL = ∆MOS и, следов., AL = MS, но AL = LS (ибо KL средняя линия ∆AHS), – следов., SM = 1/3 AM, т. е. точка S есть центр тяжести треугольника.

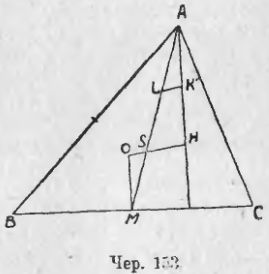
Кроме того, имеем: OS = LK = ½ SH. Поэтому:

Центр тяжести треугольника лежит на прямой, соединяющей центр описанного круга с точкою пересечения высот, причем его расстояние от центра описанного круга вдвое меньше, чем от точки высот.

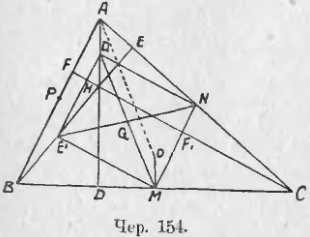
147. Пусть дан ∆ABC (чер. 154) и точки M и N сеть середины сторон BC и AC; затем пусть точка H есть точка пересечения высот AD, BE и CF и точки D1, E1 и F1 середины верхних отрезков высот. Соединим точки N и D1; тогда ND1 есть средняя линия ∆ACH и, следовательно, D1N || CF, но CF ⊥ AB и, следовательно, CF ⊥ MN, поэтому и ND1 ⊥ MN. Соединив точку D1 с M и рассматривая 4-угольник DD1NM, заключим, что около него можно описать круг (∠D1DM = d и ∠D1NM = d), центр которого должен быть расположен в середине отрезка D1M, в точке Q. Мы также найдем, что ME1 ⊥ MN, но E1D1 есть средняя линия ∆AHB и, следовательно, E1D1 || AB || MN, откуда заключаем, что E1D1NM есть прямоугольник и, следовательно, его другая диагональ E1N проходит чрез середину первой – чрез точку Q и E1N = D1M. Но E1N есть диаметр круга, проходящего чрез E, N, M, E1 (подобно тому, как D1M есть диаметр круга, проходящего чрез D, D1, N и M). Рассуждая так же, мы придем к заключению, что PF1 служит диаметром круга, проходящего чрез точки M, P, F, D1, E и F1, и PF1 пройдет чрез ту же точку Q. Отсюда несколько заключений:

1. Отрезки, соединяющие середину каждой стороны треугольника с серединою верхнего отрезка соответствующей высоты, все три равны между собою и пересекаются в одной точке.

2. Девять точек: середины сторон треугольника, основания его высот и середины верхних отрезков высот лежат на одном круге, центром которого служит выше найденная точка.

Этот круг называется кругом девяти точек или кругом Эйлера.

3. Радиус круга девяти точек вдвое меньше радиуса круга, описанного около данного треугольника.

Если O есть центр круга, описанного около ∆ ABC, то MO = AD1, откуда следует, что MD1 = OA, т. е. диаметр круга Эйлера равен радиусу круга, описанного около ∆ABC.

Можно далее найти, что точка Q (центр круга Эйлера лежит в середине отрезка HO, соединяющего точку высот с центром описанного круга. Надо рассмотреть ∆HQD1 и ∆OQM; у них: D1Q = QM, D1H = MO и ∠HD1Q = ∠QMO — следов., эти треугольники равны, откуда следует, что линия HQO прямая и что HQ = QO.