Итак, начинаем курс геометрии изучением простейших комбинаций; при этом приходится все время опираться на наблюдательность учащихся. Строим на плоскости прямую и точку; сначала точку, где придется, а затем – на прямой, и ставим вопрос, не видят ли учащиеся чего-нибудь особенного. Если точка была построена не на прямой линии, то ничего особенного не замечаем, а если учащиеся дают все-таки какие-либо ответы на этот вопрос об особенностях, то учащему приходится выяснять, что эти ответы бессодержательны. Когда точка будет взята на прямой, то учащиеся на этот вопрос отвечают (и обычно, как то показывает практика, без затруднений), что теперь прямая разделилась на 2 части: одна часть идет от точки без конца в одну сторону, а другая – в другую; эти части учащиеся показывают, проводя по ним палочкою. Даем этим частям название «луч», прямая точкою делится на 2 луча. Усложняем комбинацию: строим прямую и на ней 2 точки (теперь уже можно дать этим точкам имена: точка A, точка B); чертеж полезно располагать так, чтобы учащиеся не привыкали к чертежам, где какая-либо прямая приблизительно параллельна краю доски или странице тетради (см. чер. 10).
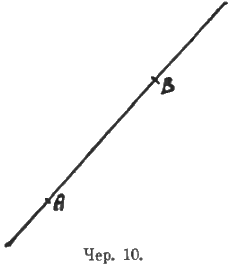
На вопрос, что теперь особенно замечается учащимися, последние отвечают, что теперь прямая линия разделилась на 3 части. Эти части показываются палочкою и учащиеся устанавливают, что две из них уже знакомы; это – лучи, идущие один от точки A без конца, а другой – от точки B, а третья часть новая – она идет от точки A до точки B. Даем ей название «отрезок» – получим отрезок AB.
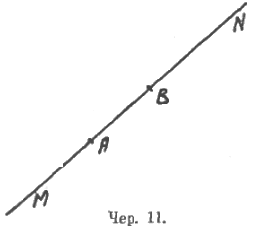
Возможно было бы попытаться (на практике я этого не делал, боясь, что еще неразвитая наблюдательность учащихся не внесет сюда отчетливости, а лишь затуманит дело) поставить дело так, чтобы учащиеся в этой комбинации видели не 3, а 5 частей (чер. 11): 1) луч AM∞, 2) луч ABN∞, 3) луч BAM∞, 4) луч BN∞ и 5) отрезок AB.
Ко всему этому изучению рассматриваемых комбинаций следует присоединить (в разные моменты) упражнения: 1) в построении прямой через 2 данные точки, 2) в построении сколько угодно лучей, исходящих из одной точки и 3) в построении отрезка без прямой. В последнем построении вводится некоторая условность: изображение ––––––––– принято считать изображением прямой линии – бесконечной, а изображение |––––––| принято считать изображением прямолинейного отрезка.
Переходим к операциям над отрезками. Прежде всего надо привести в отчетливость умение учащихся узнавать, равны ли или не равны два данные отрезка и, в последнем случае, какой из них больше и какой меньше. Для этой цели полезно провести это «сравнение отрезков» по следующей схеме: 1) берем несколько палочек, изображающих отрезки, и учащиеся при помощи некоторых операций с этими палочками устанавливают, что они умеют узнавать, равны ли или нет два данных отрезка (палочки), и отличать больший от меньшего; 2) надо научить учащихся отчетливо описывать словами, что надо делать для выполнения сравнения двух отрезков: надо один отрезок наложить (обыкновенно сначала учащиеся говорят «сложить» или «приложить» – надо показать, что эти слова здесь неуместны) на другой так, чтобы одни концы этих отрезков совпали (чтобы привести учащихся к этому, приходится показать на палочках и такое наложение, какой дано на чер. 12); 3) надо, чтобы учащиеся применили вышеизложенное словесное описание процесса выполнения сравнения двух отрезков к отрезкам, данным на чер. 13: надо наложить отрезок AB на отрезок CD так, чтобы точка A совпала с точкою C, и посмотреть, куда упадет точка B; если точка B совпадет с точкою D, то AB = CD, если точка B ляжет на самом отрезке CD (внутри его), то AB < CD, если точка B ляжет на продолжение отрезка CD (вне его), то AB > CD. Полезно бывает все это записать, хотя бы и коротко, причем учащиеся здесь ознакомятся со знаками < и >.

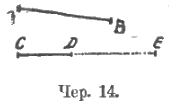
Далее учащиеся, вспоминая, что они могут иллюстрировать сложение двух чисел сдвижением двух групп (кучек) предметов (например, орехов) в одну, легко приходят к возможности выполнить сложение двух отрезков, и, конечно, сначала выполняют его на палочках, сдвигая их так, чтобы из двух отрезков (палочек) получить один. Затем переходят к чер. 14 и выясняют в конце концов (переходные стадии таковы же, как и при сравнении двух отрезков), что для сложения отрезков AB и CD надо перенести отрезок AB так, например, чтобы точка A совпала с D и самый отрезок AB пошел бы по прямой линии, на которой расположен отрезок CD (короче: по продолжению отрезка CD); если тогда точка B попадет в точку E, то DE = AB и CD + DE = CE или CD + AB = CE.
Также точно, начиная с палочек, нетрудно привести в ясность те операции, какие нужны для выполнения вычитания отрезков.
В соответствующие моменты на протяжении всех этих занятий учащиеся должны выполнить ряд упражнений. Вот наиболее существенные из них.
- Учащиеся должны ознакомиться с употреблением циркуля, как орудия, при помощи которого можно взять отрезок и переносить его куда угодно.
- Учащиеся должны на самом деле при помощи циркуля выполнить сравнение нескольких отрезков, а также сложение и вычитание.
- Учащиеся должны привыкать видеть сложение и вычитание отрезков. Так, на прилагаемом чертеже
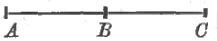 учащиеся должны видеть (и уметь это записать) и сложение двух отрезков (AB + BC = AC), причем должны показывать и каждый слагаемый отрезок и сумму, и вычитание (AC – AB = BC или AC – CB = BA), причем должны показать и уменьшаемый отрезок и вычитаемый и разность.
учащиеся должны видеть (и уметь это записать) и сложение двух отрезков (AB + BC = AC), причем должны показывать и каждый слагаемый отрезок и сумму, и вычитание (AC – AB = BC или AC – CB = BA), причем должны показать и уменьшаемый отрезок и вычитаемый и разность. - Учащиеся должны уметь данный отрезок разлагать на слагаемые, а также данный отрезок представлять в виде разности, для чего надо продолжить отрезок до какой-нибудь точки и записать, что данный отрезок есть разность двух вновь полученных отрезков.
Все эти упражнения необходимы, так как должно стремиться к тому, чтобы в будущем, когда придется иметь дело с более сложными комбинациями, учащиеся легко могли бы смотреть на известный отрезок, как на сумму или разность других отрезков.
Переходим к углам. Строится несколько раз учащимися фигура, состоящая из точки и двух лучей, из этой точки выходящих (чер. 15). Каждой из этих фигур дается название «угол».
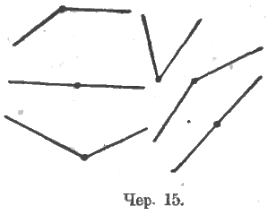
Учащиеся устанавливают, что они умеют строить угол: надо построить точку и из нее 2 луча. Вводятся названия: «вершина угла», «сторона угла»; последние показываются палочкою – ученики проводят ею от вершины по соответствующему лучу.
Выясняется, что стороны углов идут без конца, а поэтому угол остается тот же, если стороны «нарисованы» или немного длиннее или короче.
Среди углов, оказывается, имеется особый угол. Учащиеся могут установить его существование или из рассмотрения различных углов, построенных ими самими (на доске), – см. предыдущий чертеж – или при помощи опыта вращения палочки (чер. 16).

Держим палочки рукою в том месте, где они сходятся, и одну из них вращаем. Особенный угол получается тогда, когда стороны угла окажутся расположенными по прямой линии (эта особенность подмечается самими учениками и высказывается ими). Называем этот особенный угол именем «выпрямленный» или «развернутый»; показываем его вершину и стороны; строим простейшим способом выпрямленный угол (прямую линию и на ней точку). Учащиеся упражняются в обозначении углов при помощи трех букв.
Далее можно обратить внимание на тот факт (и желательно, чтобы учащиеся сами это увидали), что плоскость делится углом на 2 области (на 2 части) – см. чер. 17, где одна область затушевана. Про одну из этих областей мы говорим, что она лежит внутри угла (внутренняя область угла), а о другой, – что она лежит вне угла (внешняя область). Какую именно счесть за внутреннюю область, а какую за внешнюю – это безразлично. Если мы возьмем кусок бумаги, изображающий собою плоскость, если на нем построим угол и разрежем этот кусок по сторонам угла, то плоскость разделится на 2 части.
Чтобы рассматривать угол, приходится рассматривать одну из этих частей, а какую именно – безразлично: на каждой из них можно показать и вершину и стороны угла. Станем теперь рассматривать углы с присоединенными к ним внутренними областями (чер. 18). Чтобы на чертеже видеть, какую именно часть плоскости мы принимаем за внутреннюю область угла (и присоединяем ее к углу), условимся отмечать эту область каким-либо способом: или рисовать по этой области какую-нибудь кривую от одной стороны до другой или немного затушевывать эту область или, что в дальнейшем чаще всего будет встречаться, на этой области будем ставить ту малую букву или цифру, которыми будем иногда называть рассматриваемые углы.
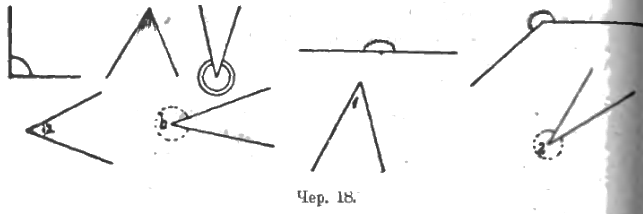
Последние 4 угла называем: угол a, угол b, угол первый, угол второй. Вводим знак, заменяющий слово «угол» и получаем ∠a, ∠b, ∠1 и ∠2.
Приступаем к сравнению углов: если имеем два угла, то можно установить, что или эти углы равны или неравны и в последнем случае один угол больше другого. Следует привести в отчетливость тот процесс наложения одного угла на другой, при помощи которого это делается. Для этой цели удобно сначала иметь дело с моделями углов, вырезанных из цветной бумаги (каждая модель дает угол с его внутреннею областью) (чер. 19).
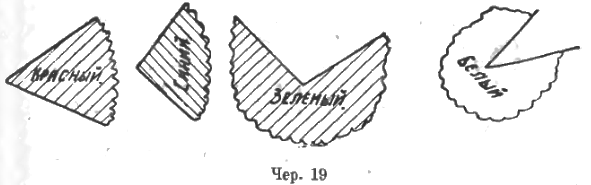
Налагаем красный угол на синий. Признаем, что синий угол больше красного, потому что при наложении одного угла на другой окажется, что красная область целиком укладывается на синей (должно ведь воображать, что там, где обрез дан зигзагообразною линиею, плоскость идет без конца), да еще часть синей остается незакрытою. Также установим, что синий меньше зеленого, что зеленый меньше белого (конечно, говоря это, мы применяемся к тому, что дано на вышеприведенном чертеже). Итак, устанавливается: для сравнения двух углов надо наложить один угол на другой так, чтобы 1) их вершины совпали, 2) совпало бы по одной стороне и 3) внутренняя область одного угла покрыла бы хотя бы часть внутренней области другого. Если окажется, что внутренние области обоих углов совпадают, то эти углы равны, а если часть внутренней области одного угла остается непокрытою, то углы неравны и тот угол больше, внутренняя область которого остается незакрытою.
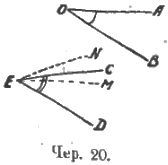
Все это можно записать, применяясь к чертежу. Например, возьмем ∠AOB и ∠CED (см. чер. 20), внутренние области которых отмечены. Перенесем ∠AOB так, чтобы точка O совпала с точкой E, чтобы сторона OB пошла пол лучу ED и чтобы внутренняя область ∠AOB пошла бы по внутренней области ∠CED. Тогда сторона OA может расположиться по разному: если OA совпадет с EC, то ∠AOB = ∠CED; если луч OA пойдет внутри ∠AOB (например, по лучу EM), то ∠AOB < ∠CED; если луч OA пойдет вне угла CED (например, во лучу EN), то ∠AOB > ∠CED.
Во время упражнений с равными и неравными углами удобно установить, в каком смысле употребляется в геометрии термин «равные фигуры».
Построив на плоскости угол, мы теперь можем считать, что получим два угла, в зависимости от того, какую из двух областей примем за внутреннюю. Если (см. чер. 21) примем за внутреннюю область затушеванную, то получим ∠a, а если незатушеванную, – то ∠b.
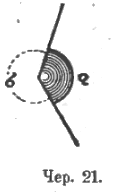
Применительно к чертежу мы получим, что ∠a < ∠b. Вообще говоря, таким способом мы получаем два неравных угла. Возникает вопрос, а не получится ли когда-нибудь два равных угла. Находится ответ: равные углы получим тогда, когда построим выпрямленный угол. Если теперь присоединим еще сюда ясное для каждого наблюдающего положение, что какие бы выпрямленные углы мы ни построили, они могут быть наложением совмещены, то явится возможность: 1) установить – «все выпрямленные углы равны между собою» и 2) разделить все углы на углы, большие выпрямленного, и на углы, меньшие выпрямленного. Вводится, наконец, условие: если построен угол и не отмечена его внутренняя область, то надо считать за эту внутреннюю область ту часть плоскости, которая дает угол, меньше выпрямленного. Это условие вводится потому, что по большей части приходится рассматривать углы, меньшие выпрямленного.
Здесь необходимы упражнения с вырезанными из бумаги моделями углов; оперируя с этими моделями, учащиеся учатся, 1) сравнивать два угла, 2) отличать сразу углы, большие выпрямленного, и углы, меньшие выпрямленного (полезно, хотя обычно это и не принято, сравнение углов не ограничивать только углами, меньшими выпрямленного). Также точно желательны упражнения вроде следующего: построен угол (например, 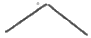 ), отметить его внутреннюю область так, чтобы получился: 1) угол, меньший выпрямленного, или чтобы получился 2) угол, больший выпрямленного.
), отметить его внутреннюю область так, чтобы получился: 1) угол, меньший выпрямленного, или чтобы получился 2) угол, больший выпрямленного.
Переходим далее к сложению и вычитанию углов. Здесь имеют место соображения, аналогичные данным при описании методики сложения и вычитания отрезков. Так же точно надо привести в отчетливость процессы сложения и вычитания углов (их описание пропускаем), выработать хотя бы некоторый навык видеть на чертеже сумму и разность углов. Так, при условии, что имеем дело лишь с углами, меньшими выпрямленного, мы на чер. 22 видим: 1) ∠AOB + ∠BOC = ∠AOC (следует каждый слагаемый угол и угол сумму показывать; при этом это показывание полезно выполнять палочкою, проводя ее, как показывает стрелка (чер. 23), по сторонам угла); 2) ∠AOC – ∠AOB = ∠BOC и 3) ∠AOC – ∠COB = ∠BOA (также надо показывать уменьшаемый угол, вычитаемый и угол разность).
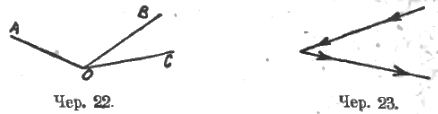
Как можно подметить, все вышеизложенное направляется идеею, что и отрезки и углы суть самостоятельные объекты, с которыми мы учимся выполнять известные операции, не стремясь сводить дело к арифметике, к числам.
Сложение и вычитание углов также должно начаться с выполнения соответствующих процессов над моделями углов, вырезанными из бумаги.
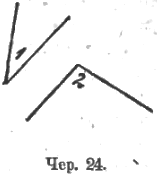
Упражнение: даны два угла, ∠1 и ∠2 (чер 24), найти их сумму (или разность), – может быть или выполняемо теперь при помощи изготовления бумажных моделей данных углов или может быть отнесено к более позднему моменту курса, к тому именно, когда будет введен в дело круг и установлена возможность строить при помощи кругов угол, равный данному.
Упражняясь над сложением углов, учащиеся могут прийти к установлению возможности случая, когда от сложения двух углов в сумме получатся выпрямленный угол. Установить такую возможность можно опять-таки при помощи операций над моделями углов, а затем построить соответствующий чертеж.
Здесь, как то уже было указано в п. 6, можно дать название «смежные» углы (чер. 25), описать их расположение (общая вершина, одна сторона общая, а две другие составляют прямую линию), но здесь нет места каким-либо доказательствам каких-либо теорем.
Далее ставится задача дополнить данный угол до выпрямленного. В п. 3 уже выяснено, что решение этой задачи приводит к установлению свойства вертикальных углов. Поэтому здесь на этом не останавливаемся.
