Мы уже имели фигуру, состоящую из двух прямых, пересекающихся в какой-либо точке (вертикальные углы). Усложним ее: присоединим к ней третью прямую, пересекающую две первых в каких-либо новых точках (чер. 38).
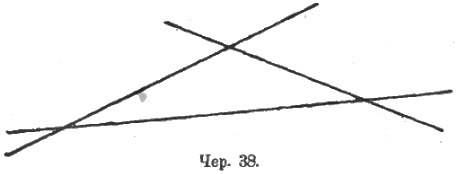
Рассматривая эту фигуру, учащиеся должны установить: 1) эта фигура состоит из 3 прямых и 3 точек их пересечения (даем названия: треугольник для всей фигуры, его стороны, его вершины); 2) на каждой прямой получается по одному отрезку (каждый из этих отрезков называется также стороною треугольника; в дальнейшем, когда придется употреблять термин «сторона», из характера вопроса делается ясным, идет ли речь о бесконечной прямой или об отрезке на этой прямой); 3) при каждой точке (вершине) определяется по 4 угла, каждый из которых меньше выпрямленного; 4) плоскость делится на 7 областей, из которых 6 уходят в бесконечность, а 7-ая ограничена со всех сторон – эта последняя часть называется площадью треугольника. После этого явится возможным выделить их вышеуказанных 12 углов те, внутри которых лежит площадь треугольника, – называем эти углы внутренними углами треугольника.
Так как во многих вопросах приходится рассматривать только отрезки сторон между вершинами и только внутренние углы, то общеупотребителен сокращенный чертеж треугольника (чер. 38-а).
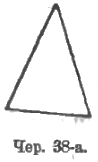
Если бы понадобился ответ на вопрос, что называется треугольником, то все предыдущее приводит к ответу, что треугольником называется фигура, состоящая из трех прямых, пересекающихся в трех точках. Однако, чтобы работать над треугольником, нет надобности в определении, а достаточно сознания: я умею строить треугольник, причем возможно (на это важно обратить внимание) двоякое начало построения: 1) можно начать с построения трех точек (вершин), и они, взятые попарно, определят 3 прямых (стороны треугольника); 2) можно начать с построения трех прямых, и тогда само собою определяются 3 вершины треугольника.
Ставим на очередь задачу: построить треугольник, имеющий стороны, равные сторонам данного треугольника (под именем «сторона» здесь понимается отрезок).
При помощи циркуля решаем задачу, и полезно выполнить 2 построения, в двух разных местах плоскости.
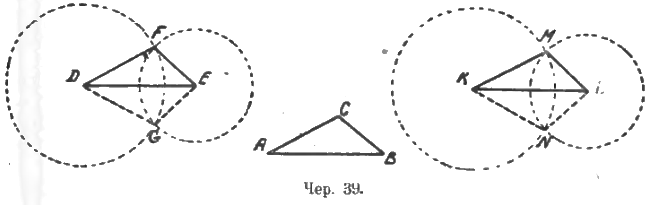
Наблюдательность должна здесь привести к следующим заключениям (чер. 39):
- При всяком построении получаются два треугольника (напр., ∆DFE и ∆DGE). Так как фигура, состоящая их двух кругов, имеет ось симметрии (DE или для другой фигуры KL), то ∆DFE при перегибании по оси симметрии совпадет с ∆DGE – всякий раз, следовательно, получается 2 равных треугольника.
- Систему кругов с центрами K и L можно совместить с системою кругов D и E (ибо KL = DE и радиусы кругов попарно одинаковы); поэтому ∆KML должен совместиться с ∆DFE и ∆KLN с ∆DGE, т. е. все треугольники с равными сторонами должны быть равны между собою. Получаем, следовательно, основной признак равенства треугольников: если стороны одного треугольника равны соответственно сторонам другого, то эти треугольники равны.
Выяснение двух других основных признаков равенства треугольников полезно начать с изучения процесса наложения одного треугольника на другой: 1) если у них есть по одному равному углу и 2) если у них есть по одной равной стороне.
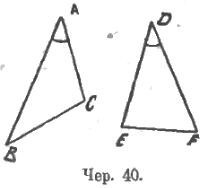
Напр., построим 2 треугольника ∆ABC и ∆DEF (чер. 40) так, чтобы ∠D = ∠A, но AB > DE и AC < DF. Учащиеся должны нарисовать, как расположится ∆DEF, если его наложить на ∆ABC при условии совмещения равных углов. Далее, деформируя стороны DE и DF треугольника DEF, учащиеся должны установить, что для совпадения этого треугольника с ∆ABC достаточно так изменить стороны DE и DF, чтобы DE = AB и DF = AC.
Так же разбирается и случай равенства треугольников по стороне и двум прилегающим к ней углам. Случай равенства треугольников по двум сторонам и углу против большей из них вводить в курс вовсе не нужно – это возможно лишь по окончании общего курса геометрии для тех, кто специально хочет заниматься геометриею.
Учащиеся должны освоиться с мыслью, что раз удалось установить равенство треугольников по равенству трех элементов этих треугольников, то и остальные элементы их равны; должны также освоиться с тем как находить равные элементы (против равных сторон лежат равные углы и обратно). Учащиеся должны также упражняться в построениях треугольников: 1) по трем данным сторонам, причем они должны здесь подметить невозможность при известных условиях этого построения; 2) по двум сторонам и углу между ними и 3) по стороне и двум прилегающим углам – здесь должно остановиться на случае, когда сумма двух данных углов равна выпрямленному углу, и связать этот случай с тем, что они уже знают о параллельных прямых; также нельзя пропускать случая, когда сумма двух данных углов больше выпрямленного.
Во время этих построений явится возможность построения и равнобедренного и равностороннего треугольника, и явится потребность их изучения.
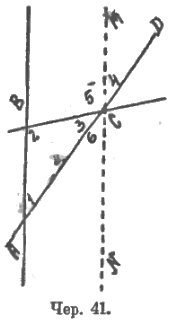
Далее мы подмечаем, что когда построен треугольник, то является случай применить построение прямой, параллельной данной, через данную точку (чер. 41.). Напр., имеется прямая AB и точка C вне ее. Построим прямую CM ║ AB, для чего можно воспользоваться или секущею CB и построить ∠5 = ∠2 или секущею AC и построить ∠6 = ∠1, мы должны добиться от учащихся отчетливого видения: 1) равных углов (∠5 = ∠2, ∠6 = ∠1, ∠4 = ∠1 и т. п.), 2) что при точке C выполнено сложение углов, напр., ∠6 + ∠3 + ∠5 = выпрям. углу (или ∠4 + ∠5 +∠3 = выпрям. углу).
Отсюда, заменяя ∠6 углом 1-м и ∠5 углом 2-м, получим:
∠1 + ∠3 + ∠2 = выпрям. углу, т. е. хотя ∠1, ∠2 и ∠3 на чертеже и не сложены, тем не менее, их сумма вполне определена и всегда равна выпрямленному углу.
Далее здесь же можно остановиться на внешнем угле треугольника (∠BCD) и увидать, что ∠BCD = ∠5 + ∠4 = ∠2 + ∠1.
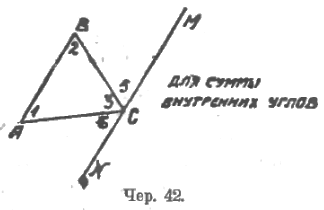
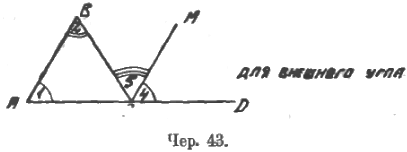
Полезно те части всего вышеприведенного чертежа, на какие надо в данный момент обратить особенное внимание, 1) обрисовывать цветным карандашом (напр., отрезки AB, BC, CA и прямую NM, – здесь ведь надо обратить особое внимание, лишь на внутренние углы при точках A и B и на равенство их углам 6-му и 5-му) и 2) давать частичные чертежи для рассматриваемого вопроса (чер. 42 и 43).
Необходимо также разнообразить построение, строя прямую, параллельную одной стороне треугольника, то через точку A, то через точку B, то через точку C.
