Напомнив учащимся, что прямая линия определяется двумя точками, и обратив их внимание на то, что до сих пор мы имели дело с прямыми, имеющими одну общую точку (пересекающимися в одной точке), явится возможным поставить на очередь вопрос: а нельзя ли построить две прямые так, чтобы они вовсе не имели общих точек (не пересекались бы?). Хорошо, конечно, было бы провести предварительную беседу так, чтобы этот вопрос пришел на мысль самим учащимся.

Придется здесь не добиваться, чтобы учащиеся сами нашли ответ на этот вопрос, а дать его в готовом виде, причем предварительно придется упражнять учащихся в рисовании зигзагов вроде (чер. 31):

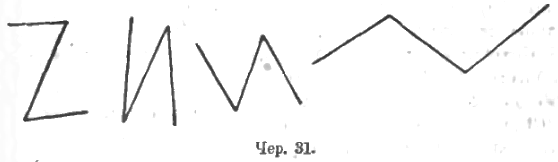
Даем получаемым здесь углам название внутренние накрест лежащие. Добиваемся, чтобы образ этих углов запечатлелся в воображении учащихся.

Затем ставим интересующий нас вопрос в такой форме. (Другая форма изложения дана в моей «Геометрии на плоскости», 3-е издание.) Имеем прямую AB и точку C вне ее, – нельзя ли построить через точку C такую прямую, чтобы она не пересекалась с AB (не имела бы общих точек?). Сообщаем учащимся следующее построение (чер. 32).

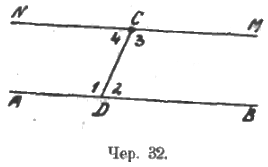
Строим: 1) через C любую прямую к какой-либо точке D прямой AB (короче: секущую CD), – получим ∠1 и ∠2; 2) принимая точку C за вершину, ∠3 = ∠1 так, чтобы эти углы были внутренние накрест лежащие, – получаем луч CM; 3) луч CN, продолжение CM, – получаем прямую NM и ∠4. Разучим полученную фигуру.

Мы видим: 1) ∠1 и ∠2 углы смежные или ∠1 + ∠2 = выпрям. ∠
2) ∠3 и ∠4 углы смежные или ∠3 + ∠4 = выпрям. ∠

Мы знаем (так строили): ∠3 = ∠1.

Отсюда заключаем: ∠4 = ∠2.

(Две суммы равны и у них по одному слагаемому имеем заведомо равными, след., и другие слагаемые должны быть равны.)

На основании этого устанавливаем:

Если построено две прямых, пересеченных секущею так, чтобы пара внутренних накрест лежащих углов была равна, то и другая их пара тоже состоит из равных углов.

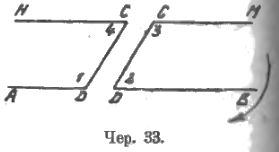
Продолжая изучение фигуры дальше, изображаем ее разрезанной по секущей CD и получаем две фигуры: левую NCDA и правую MCDB (чер. 33). Полезно иллюстрировать, как это разрезание, так и дальнейшее полоскою бумаги. Поворачиваем правую фигуру и накладываем ее на левую, чтобы точка D правой совпала с точкой C левой и точка C правой с точкой D левой. Принимая во внимание, что ∠1 = ∠3 и ∠2 = ∠4, мы убеждаемся, что левая и правая фигура совпадают при наложении, т. е. они равны. Отсюда уже легко видеть, что прямая NM не может иметь общей точки с прямой AB: если бы кто подумал, что эта общая точка расположена вправо от секущей CD, то, в силу равенства фигур, такая же общая точка должна была бы быть и влево, т. е. через две точки проходило бы две прямых, что невозможно. Вводим термин «параллельные» прямые и устанавливаем:

1. Через точку вне прямой можно построить прямую, параллельную данной (остается открытым вопрос: сколько?).
2. Если две прямых пересечены секущею и оказалось, что внутренние накрест лежащие углы равны, то эти две прямых параллельны.

Следует упражнять учащихся в построении через данную точку прямой, параллельной данной, при различном их расположении (чер. 34):

Затем является возможным поставить на очередь вопрос: сколько можно построить через точку C прямых, параллельных прямой AB? Исходным пунктом может послужить то обстоятельство, что для построения параллельной надо из точки C строить сначала секущую CD, а ее можно построить по разному, – возникает вопрос, будут ли или нет все получаемые прямые совпадать с прямой NM? Ответ на этот вопрос дается только на основании представления, и получаем постулат Евклида о параллельных в форме, которая теперь пользуется наибольшим распространением: через точку вне прямой можно построить лишь одну прямую, параллельную данной.

Мимоходом придется рассмотреть два следствия из этого постулата: 1) если прямая пересекает одну из параллельных, то она пересекает и другую и 2) две прямые, параллельные в отдельности третьей, параллельны между собою. По поводу последнего их них следует заметить, что учащиеся сейчас же соглашаются признать его справедливость, но возникает сомнение, делают ли они это на основе яркого представления или на основе слов «две прямые, параллельные 3-ей, параллельны между собою». Чтобы показать им необходимость разобраться в этом вопросе, полезно обратиться к соотношениям, имеющим место в жизни: 1) если 2 человека знакомы каждый с третьим, то следует ли отсюда, что эти два человека знакомы между собою? 2) Если 2 лица суть родственники третьему, то обязательно ли, чтобы эти 2 лица были и между собою родственники?

Больше внимания надо уделить третьему следствию из постулата: если построены 2 параллельных прямых и пересечены какою-либо секущею, то обязательно внутренние накрест лежащие углы равны между собою.

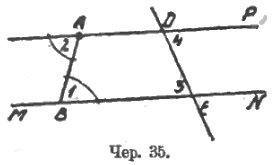
Дело можно поставить следующим образом. Пусть надо через точку A построить прямую, параллельную MN (чер. 35). Строим секущую AB и ∠2 = ∠1; тогда AP ║ MN. Пересечем затем наши параллельные новой секущей DE; возникает вопрос, будут ли равны между собою, напр., ∠3 и ∠4.

Следующее соображение (доказательством его не следует называть) дает ответ на этот вопрос. Если бы мы взяли сначала не точку A, а точку D, и через нее захотели бы построить прямую, параллельную MN, то могли бы воспользоваться секущей DE и должны были бы при точке D построить угол, равный ∠3, и внутренний накрест лежащий с ним, и тогда пришли бы к той же прямой ADP, потому что через точку D можно построить лишь одну прямую ║ MN. Это указывает на необходимость того, чтобы ∠4 = ∠3.

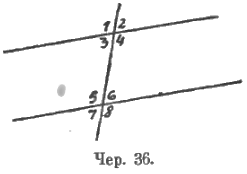
Далее явится возможным рассмотреть все 8 углов, получаемых от пересечения параллельных секущею. Ясно, что их можно разделить на 2 группы, равные между собою (чер. 36):

1) ∠1 = ∠4 (вертикальные) = ∠5 (внутр. накр. лежащие) = ∠8 (вертикальные).

2) ∠2 = ∠3 (вертик.) = ∠6 (вн. накр. леж.) = ∠7 (верт.).

Но угол одной группы не обязан равняться углу другой.

Далее мы видим, что, напр., ∠1 и ∠2 сложены между собою и их сумма есть выпрямленный угол, т. е. ∠1 и ∠2 = выпрямл. углу.

Если здесь ∠1 или ∠2 или оба заменить каким-либо равным углом (из тоже же группы, к какой этот ∠ принадлежит), то сумма не изменится.

Напр. ∠1 + ∠2 = выпр. углу, но ∠1 можно заменить равным ему ∠8-м и ∠2 углом 3-м. Получим: ∠8 + ∠3 = выпр. углу.

Устанавливается общее положение: если возьмем один угол из одной группы и один из другой, то их сумма равна выпрямленному углу.

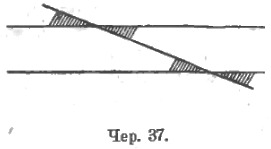
Следует учащихся упражнять в умении при разных обстоятельствах ясно отличать углы этих двух групп, для чего полезно требовать от их чертежей (от руки) вроде следующего (чер. 37) (углы одной группы затушеваны).

Во время этих упражнений явится возможность ввести в дело и внешние накрест лежащие углы и соответственные и внутренние (или внешние) односторонние и устанавливать их свойства.

Также явится возможным изменить и способ построения параллельных прямых, так как станет ясным, что вовсе не обязательно строить равные внутренние накрест лежащие углы, а можно получить параллельные прямые и при помощи построения равных соответственных углов или равных внешних накрест лежащих.

Наконец, придется остановиться на рассмотрении углов с попарно параллельными сторонами.