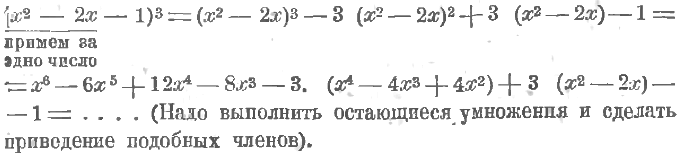Станем опять сначала на точку зрения арифметики и рассмотрим возведение в куб суммы и разности двух чисел. Получим:
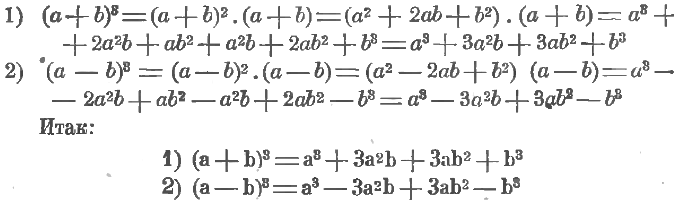
Словами эти равенства читаются так:
1) Куб суммы двух чисел равняется кубу первого числа, плюс произведение тройки на квадрат первого числа и на второе число, плюс произведение тройки на первое число и на квадрат второго числа, плюс куб второго числа.
2) Куб разности двух числе равен кубу первого числа, минус произведение тройки на квадрат первого числа и на второе, плюс произведение тройки на первое число и на квадрат второго, минус куб второго числа.
Теперь мы можем сразу написать, что, например,
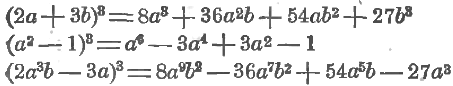
Здесь сначала написан куб первого числа, т. е. (2a3b)3, а это = 8a9b3, затем «минус произведение 2 на квадрат первого числа и на второе», т. е. –3 ∙ (2a³b)² ∙ (3a)= –3 ∙ 4a6b2 ∙ 3a = – 36a7b2, затем «плюс произведение тройки на первое число и на квадрат второго», т. е. +3 ∙ (2a³b) ∙ (3a)² = +3 ∙ 2a3b ∙ 9a2 = 54a5b, наконец, «минус куб второго числа», т. е. –(3a)3 = –27a3.
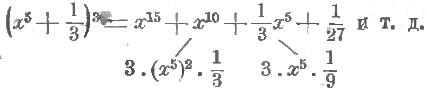
Мы можем наши равенства переписать в виде:
1) (a + b)³ = (+a)³ + (+3) (+a)² (+b) + (+3) (+a) (+b)² + (+b)³
2) (a – b)³ = (+a)³ + (+3) (+a)² (–b) + (+3) (+a) (–b)² + (–b)³
и читаем их так:
Куб двучлена равен кубу первого члена, плюс произведение числа (+3) на квадрат первого члена и на второй, плюс произведение числа (+3) на первый член и на квадрат второго, плюс куб второго члена.
Например: (–3a4 – ab)3 = (–3a4)3 + (+3) (–3a4)2 (–ab) + (–3a4) (–ab)2 + (–ab)3 = –27a12 – 27a9b – 3a5b2 – a3b3 и т. п.
Если потребуется возвести в куб трехчлен, то можно или сводить дело к умножению
[Например: (x² – 2x – 1)³ = (x² – 2x – 1)(x² – 2x – 1)(x² – 2x – 1) = …]
или, приняв временно два члена (лучше первые два) за одно число, свести дело к возведению в куб двучлена: