Арифметические дроби обладают свойством, которое позволяет: 1) упрощать дроби и 2) выполнять их сложение и вычитание; это свойство таково: если числителя знаменателя дроби умножить или разделить на одно и то же число, то вновь получаемая дробь равна прежней (напр., 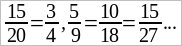 ).
).
Возникает вопрос, останется ли в силе это свойство и для алгебраических дробей. Рассмотрим сначала выражения вроде следующих:
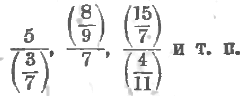
Эти выражения являются обобщением арифметических дробей: числители и знаменатели их еще остаются арифметическими числами, но уже не обязательно целые, а могут быть и дробными. Напр., выражение
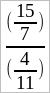
рассматривается как дробь, у которой числитель есть дробное число  и знаменатель – дробь
и знаменатель – дробь 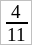 . Подобные выражения называют сложными дробями.
. Подобные выражения называют сложными дробями.
Выполняя деление, указанное в этих сложных дробях, мы получим:
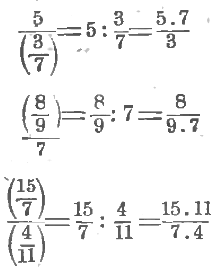
Попробуем теперь числителя и знаменателя каждой из этих сложных дробей умножить на одно и то же число, сначала на целое:

Попробуем теперь числителя и знаменателя третьей сложной дроби умножить на одно и то же дробное число:

Мы видим, что и к сложным дробям рассматриваемое свойство применимо. Можно, и не выполняя всех действий, прийти к тому же результату: если числителя сложной дроби

умножить на какое-нибудь число (целое ли или дробное – теперь безразлично), то это равносильно тому, что все выражение (всю сложную дробь, или, другими словами, то число, которому равно это выражение) умножить на это число; если затем знаменателя этой сложной дроби умножить на то же число, то это равносильно тому, что все выражение разделится на это число; если какое-нибудь число умножить сначала на новое число, а потом разделить на него же, то оно останется, в общем, без перемены. Итак, мы теперь можем написать:
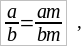
где a, b и m суть какие-нибудь арифметические числа, целые или дробные – безразлично.
Остается теперь сообразить, будет ли справедливо это равенство, если a, b и m будут относительными числами?
Так как положительные числа считаются совпадающими с арифметическими, то это равенство остается в силе, если a, b и m суть относительные положительные числа. Станем теперь предполагать некоторые из них отрицательными и рассматривать, остается ли наше равенство справедливым. Абсолютные величины выражений 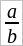 и
и 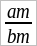 должны быть одинаковы, так как абсолютные величины суть арифметические числа. Если и a и b отрицательны, то дробь
должны быть одинаковы, так как абсолютные величины суть арифметические числа. Если и a и b отрицательны, то дробь 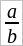 выражает положительное число, но и дробь
выражает положительное число, но и дробь 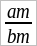 выражает также положительное число, каков бы знак ни был у числа m (напр., если m число отрицательное, то am число положительное, bm – тоже положительное и частное от деления am на bm тоже положительное), т. е. равенство остается верным. Если a и b имеют разные знаки, то частное
выражает также положительное число, каков бы знак ни был у числа m (напр., если m число отрицательное, то am число положительное, bm – тоже положительное и частное от деления am на bm тоже положительное), т. е. равенство остается верным. Если a и b имеют разные знаки, то частное 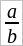 выражает отрицательное число, но и частное
выражает отрицательное число, но и частное 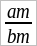 в этом случае, каково бы ни было число m, выражает отрицательное число (напр., если a и m положительные числа, а b отрицательное, то am положительное число, bm – отрицательное и частное от деления am на bm – отрицательное).
в этом случае, каково бы ни было число m, выражает отрицательное число (напр., если a и m положительные числа, а b отрицательное, то am положительное число, bm – отрицательное и частное от деления am на bm – отрицательное).
Итак, всегда справедливо равенство:
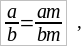
каковы бы числа a, b и m ни были.
То же равенство можно написать в обратном порядке:
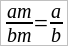
Итак, основное свойство дробей, что их числителя и знаменателя можно умножать на одно и то же число (на какое угодно относительное число), распространяется и на алгебраические дроби.
