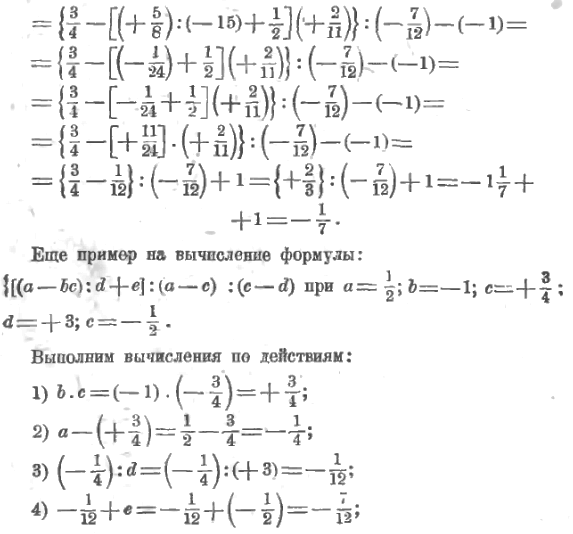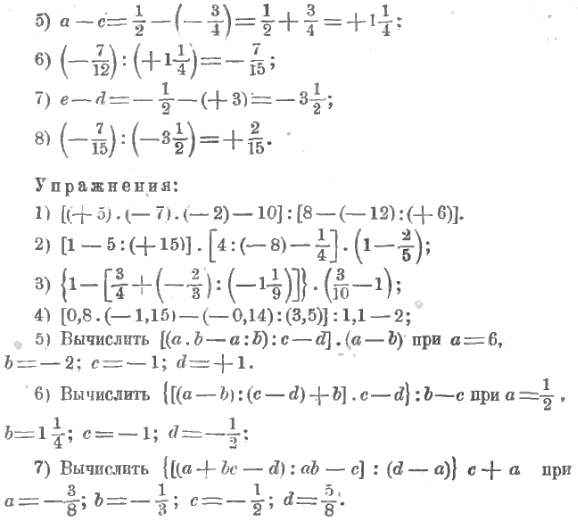Деление мы можем рассматривать, как действие, обратное умножению, при помощи которого по данному произведению и по одном множителю находят другой множитель. Данное произведение пишется перед знаком деления, а данный множитель после этого знака.
Пусть требуется
(+24) ÷ (+6).
Здесь +24 есть произведение и +6 один множитель, – надо найти другой. Так как абсолютная величина произведения (24) получается, как знаем из предыдущего, умножением абсолютной величины одного множителя (6) на абсолютную величину другого, то, чтобы найти последнюю, надо арифметически разделить число 24 на число 6, – получим 4. Следовательно, абсолютная величина искомого множителя = 4. Чтобы найти его знак, обратим внимание на знак произведения: так как у произведения знак +, то у множителей должны быть одинаковые знаки; у одного из них мы видим знак +, следовательно, и у другого должен быть знак +. Итак,
(+24) ÷ (+6) = +4.
Пусть требуется
(+24) ÷ (–6).
Абсолютная величина искомого множителя, как выяснено выше, = 4. У произведения знак +, следовательно, у множителей одинаковые знаки; у одного из них мы видим знак – (–6), следовательно, и у другого должен быть знак –. Итак,
(+24) ÷ (–6) = –4.
Пусть требуется
(–24) ÷ (+6).
Абсолютная величина искомого множителя также = 4. У произведения знак –, следовательно, у множителей были знаки разные: у одного из них мы видим знак + (+6), следовательно, у другого должен быть знак –. Итак,
(–24) ÷ (+6) = –4.
Пусть требуется
(–24) ÷ (–6).
Абсолютная величина искомого множителя также = 4. У произведения знак –, следовательно, у множителей были разные знаки; у одного из них видим знак – (–6), следовательно, у другого был знак +. Итак,
(–24) ÷ (–6) = +4.
Разобранные 4 случая обнимают всевозможные комбинации знаков у данных чисел:
(+24) ÷ (+6) = +4
(+24) ÷ (–6) = –4
(–24) ÷ (+6) = –4
(–24) ÷ (–6) = +4
Вспомнив, что данное произведение называется делимым, данный множитель – делителем и искомый множитель – частным, мы можем теперь установить:
чтобы разделить одно относительное число на другое, надо разделить их абсолютные величины и у частного поставить знак +, если делимое и делитель были с одинаковыми знаками; если же они были с разными знаками, то поставить знак –.
Пример на вычисление:
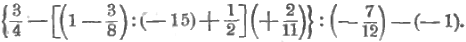
Заметим, что если порядок действий не обозначен скобками, то деление (так же, как и умножение) надо выполнить раньше сложения или вычитания. Поэтому