Умножение
3. Следующее действие, умножение, появляется в курсе целых чисел, как действие, заменяющее сложение равных слагаемых. В курсе дробей выясняется необходимость расширить понятие об умножении и установить смысл умножения на дробь, как действия, при помощи которого некоторая часть числа берется слагаемым несколько раз. Напр.:
a ∙ 4 = a + a + a + a
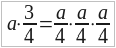 .
.
Вспомнив названия «множители» и «произведение», мы будем иметь возможность формулу a∙b (или просто ab, так как условились для упрощения пропускать знак умножения, точку, тогда, когда один множитель или оба выражены буквами) прочесть: произведение чисел a и b.
Вот более сложные формулы: 1) ab + cd «сумма двух произведений» (или «сумма произведений двух пар чисел» и т. п.); 2) (a + b)(c + d) «произведение суммы чисел a и b на сумму чисел c и d» (или «произведение сумм двух пар чисел»); 3) (a + b)(c + d) «произведение суммы двух чисел на разность тех же чисел»; 4) ab – 1 «разность между произведением чисел a и b и числом 1» и т. п.
Переместительный закон умножения («произведение не изменяется от перестановки множителей») выразится равенством:
ab = ba.
Если возьмем, напр., числа 3 и 4, то справедливость его ясна из рассмотрения, напр., следующей группы кружков

Если разуметь под a и b целые числа, каждое из которых меньше 10, то формула 10a + b выражает двузначное число, в котором a десятков и b единиц: в 1 десятке 10 единиц, в a десятках 10 ∙ a единиц, да еще b единиц, а всего (10 ∙ a + b) единиц (желательно повторить те же рассуждения для числа, напр., 79). Также точно, установив вышеуказанные ограничения для букв c и d, получим:
100a + 10b + c... формулу, выражающую трехзначное число, в котором a сотен, b десятков и c единиц,
1000a + 100b + 10c + d... формулу, выражающую четырехзначное число, и т. д.
5. Подобно тому, как сложение нескольких чисел считается за одно действие, так точно и умножение многих множителей удобно выполнять сразу и считать за одно действие.
(Если среди множителей имеются дроби, напр., 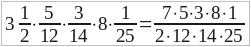 , выполняем сокращения и получаем ответ сразу.)
, выполняем сокращения и получаем ответ сразу.)
Поэтому формула
abcde
выражает «произведение 5 множителей».
Также точно: 1) (a + b)(c + d)(e + f)... произведение сумм трех пар чисел; 2) a(a + b)(a – b)... произведение числа a, на сумму чисел a и b и на разность тех же чисел; 3) если a целое число, то формула a(a + 1)(a + 2)(a + 3) выражает произведение четырех последовательных чисел и т. п.
Арифметика учит нас, что перемножать числа можно в любом порядке и любыми группами. Напр.:
abcde = cebda = (cd) ∙ (ae) ∙ b = . . . . .
Деление
4. Подобно тому, как это было сделано для вычитания, является возможность установить, что 2 вопроса:
1) ? × 11 = 143
и 2) 11 × ? = 143
(1) задумано число, умножено на 11, получилось 143, – какое число задумано? и 2) на какое число надо умножить 11, чтобы получить 143?) дают начало новому действию, делению. В силу переместительного закона умножения оба вопроса решаются одним и тем же действием 143 ÷ 11. Отсюда устанавливаем, что деление есть действие, обратное умножению, при помощи которого по данному произведению и по одному множителю находится другой.
Если написана формула a ÷ b или 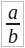 , то a есть данное произведение, b данный множитель, – надо найти другой множитель. Вспоминая название «делимое», «делитель» и «частное», мы можем прочесть предыдущую формулу словами: «частное чисел a и b».
, то a есть данное произведение, b данный множитель, – надо найти другой множитель. Вспоминая название «делимое», «делитель» и «частное», мы можем прочесть предыдущую формулу словами: «частное чисел a и b».
Более сложные формулы: 1) 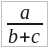 «частное от деления числа a на сумму чисел b и c», 2)
«частное от деления числа a на сумму чисел b и c», 2) 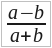 «частное от деления разности двух чисел на сумму тех же чисел», 3) (ab + cd) ÷ (a + b + c + d) «частное, причем делимым служит сумма произведений двух пар чисел, а делителем – сумма всех этих четырех чисел» и т. п.
«частное от деления разности двух чисел на сумму тех же чисел», 3) (ab + cd) ÷ (a + b + c + d) «частное, причем делимым служит сумма произведений двух пар чисел, а делителем – сумма всех этих четырех чисел» и т. п.
