Возьмем сначала какое-либо положительное число, напр., +3, и станем его возводить в разные степени:
(+3)² = (+3) ∙ (+3) = +9; (+3)³ = (+3) ∙ (+3) ∙ (+3) = +27; (+3)4 = (+3) ∙ (+3) ∙ (+3) ∙ (+3) = +81 и т.д.
Из этих примеров уже становится совершенно ясным, что при возведении в любую степень положительного числа результат всегда получается положительным.
Возьмем затем отрицательное число, напр., –3, и станем его возводить в разные степени:
(–3)² = (–3) ∙ (–3) = +9; (–3)³ = (–3) ∙ (–3) ∙ (–3) = –27; (–3)4 = (–3) ∙ (–3) ∙ (–3) ∙ (–3) = +81; (–3)5 = (–3) ∙ (–3) ∙ (–3) ∙ (–3) ∙ (–3) = –243 и т. д.
Рассматривая эти примеры, придем к общему заключению, что при возведении отрицательного числа в четную степень (во 2-ую, в 4-ую, в 6-ую и т. д.) результат получается положительный, а при возведении его в нечетную степень (в 3-ю, в 5-ую, в 7-ую и т. д.) результат получается отрицательным.
Вот еще примеры:
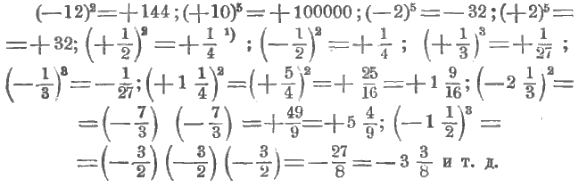
Выполним два примера на вычисление, где помимо, возведения в степень, входят и другие действия.
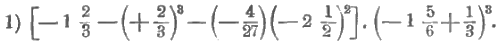
Сначала надо выполнить действия внутри каждых скобок, причем внутри квадратных скобок пришлось бы сначала выполнить умножение  , но второй множитель еще не вычислен – надо, поэтому, предварительно вычислить его. Итак,
, но второй множитель еще не вычислен – надо, поэтому, предварительно вычислить его. Итак,
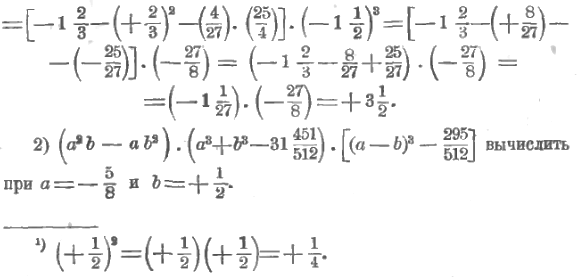
Будем вычислять по множителям. Первый множитель есть a²b – ab². Здесь написана разность между произведением квадрата числа a на число b и произведением числа a на квадрат числа b. Согласно этому, и следует вести вычисления: сначала число a возвести в квадрат, полученный результат умножить на число b, – получим уменьшаемое; затем число b возвести в квадрат, умножить число a на полученный результат, – получим вычитаемое, после чего надо выполнить вычитание:

Действия, обратные возведению в степень, будут разучиваться в дальнейшем курсе.
