55. Уравнение с двумя неизвестными. Рассмотрим теперь уравнение

5x + 3y = 18.

Оно является записью задачи: найти числовые значения для x и y, чтобы двучлен 5x + 3y оказался равным числу 18.

Мы знаем, что если бы в этом двучлене было бы лишь одно неизвестное число, то и тогда мы сумели бы решить соответствующее уравнение. Поэтому возникает соображение, что здесь одно из неизвестных является как бы лишним: если взамен неизвестного y, например, взять какое угодно число, то мы получим уравнение с одним неизвестным.

А если так, то данное уравнение должно иметь сколько угодно решений, и выясняется способ их получения: станем давать одному из неизвестных, например, y, произвольные значения и всякий раз из получаемого уравнения с 1 неизвестным станем определять другое неизвестное x. Чтобы придать этой работе больше порядка, будем результаты ее записывать в таблице.

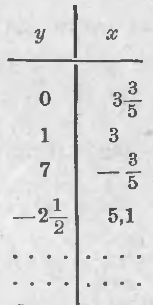
Дадим y значение 0, т. е. примем, что y = 0 (записано в первой строчке таблицы). Тогда наше уравнение обратится в

5x = 18,

откуда

x = 3(3/5)

(в таблице записываем это число во втором столбце, озаглавленном буквою x).

Итак, мы получили одно решение нашего уравнения: y = 0 и x = 3(3/5) (если эти значения подставить в наш двучлен вместо x и y, то требование, чтобы двучлен равнялся числу 18, оправдается:
3 * 3(3/5) + 3 * 0 = 18).

Дадим y значение 1, т. е. примем, что y = 1 (вторая строчка таблицы); тогда получим

5x + 3 = 18,

откуда 5x = 18 – 3 или 5x = 15 и x = 3 (записано во 2-ой строчке). Итак, найдено второе решение уравнения y = 1 и x = 3.

Дадим y значение 7, т. е. примем, что y = 7; тогда получим уравнение 5x + 21 = 18, откуда 5x = –3 и x = –3/5 (см. 3-ю строчку таблицы).

Примем еще y = –2½; тогда 5x + 3(–2½) = 18 или 5x – 7½ = 18, откуда 5x = 25½ и x = 5(1/10) = 5,1 (см. 4-ю строчку таблицы). Эту работу можно продолжить сколь угодно далеко. Итак, одно уравнение с двумя неизвестными имеет бесконечно много решений; для их получения надо одному неизвестному давать произвольные значения и из получаемых уравнений определять всякий раз другое неизвестное.

Рассматривая предыдущую таблицу и вспоминая п. 49, мы установим: у нас y был независимым переменным, x — зависимым, или x является функцией y – a.

Мы можем несколько ускорить работу нахождения решений данного уравнения. Сочтем y за известное число (все равно, ведь, y мы всякий раз заменяли известным числом); тогда на уравнение 5x + 3y = 18 мы можем смотреть, как на уравнение с одним неизвестным x и решим это уравнение:

5x = 18 – 3y; x = (18 – 3y) / 5

Мы можем этот результат выразить словами так: мы из данного уравнения определили y через x.

Теперь по формуле (18 – 3y) / 5 мы можем легко найти сколько угодно решений, делая вычисления в уме. Примем, например, y = 2. Тогда надо (–3) умножить на (+2), получим –6; сложить (+18) и (–6) — получим +12 и разделить на 5 — получим x = +2(2/5). Еще пусть y = 10; тогда (–3) · (+10) = –30; (+18) + (–30) = –12; (–12) : (+5) = –2(2/5), т. е. x = –2(2/5) и т. д.

Возьмем еще уравнение:

5x – 3y = 17.

Примем за независимое переменное x, а за зависимое y и определим y через x. Это можно сделать двумя приемами:

 

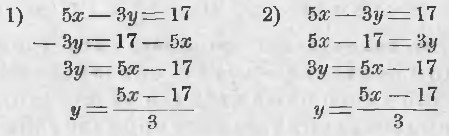
Быть может второй прием удобнее 1-го, так как его выполнение легче поддается воображению, если желательно выполнить определение y-а через x в уме.

Теперь мы можем найти сколько угодно решений нашего уравнения: 1) x = 0; y = –5(2/3); 2) x = 1; y = –4; 3) x = –1; y = –7(1/3) и т. д.

Следует приучиться быстро (в уме) определять одно из неизвестных данного уравнения с двумя неизвестными через другое. Примеры:
f55_3

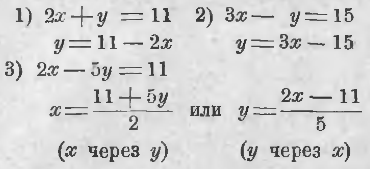
и т. д.