Мы легко найдем:

(5a³b)² = 5a³b ∙ 5a³b = 25a⁶b²
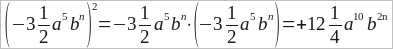 и т. п.

Однако, следует писать результат сразу, не записывая промежуточных умножений, напр.

(–ab²c³)² = +a²b⁴c⁶ и т. п.

Наблюдая выполненные примеры, мы придем к заключению, что при возведении одночлена в квадрат следует: 1) возвести в квадрат его коэффициент и 2) показателя степени каждого множителя удвоить (или умножить на 2).

Также

(5a³b)³ = 5a³b ∙ 5a³b ∙ 5a³b = 125a⁹b³

(–2ab⁴)³ = –2ab⁴ ∙ (–2ab⁴) ∙ (–2ab⁴) = –8a³b¹² и т. п.

Из этих примеров мы придем к заключению, что при возведении одночлена в куб следует коэффициент возвести в куб, а показателя степени каждого множителя умножить на 3.

Результат следует писать сразу.

Напр.,

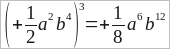 и т. п.

Теперь уже не трудно сообразить, что при возведении одночлена, напр., в 5-ую степень следует коэффициент возвести в 5-ую степень, а показателей степеней каждого множителя умножить на 5 и т. п.

(a³)⁵ = a¹⁵; (x⁴)⁴ = x¹⁶; (y⁵)⁶ = y³⁰
и вообще (a^m)ⁿ = a^mn, т. е.

при возведении степени в новую степень показатели перемножаются.

Также:

(+2ab³)⁵ = +32a⁵b¹⁵; (–2ab³)⁵ = –32a⁵b¹⁵

(+2ab³)⁶ = +64a⁶b¹⁸; (–2ab³)⁶ = +64a⁶b¹⁸ и т. п.