В предыдущем мы имели много примеров, в которых, при помощи нашего знания о значении коэффициентов, мы более короткий многочлен заменяли более длинным.
Так, трехчлен 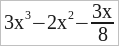 был заменен восьмичленом
был заменен восьмичленом 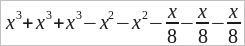 . Но в большинстве случаев приходится пользоваться обратным преобразованием многочлена: пользуясь смыслом коэффициента, можно уменьшать число членов многочлена. Вот простейшие примеры:
. Но в большинстве случаев приходится пользоваться обратным преобразованием многочлена: пользуясь смыслом коэффициента, можно уменьшать число членов многочлена. Вот простейшие примеры:
a + a + a + a – b – b – b = 4a – 3b
x – y – y + x – y – y + x = 3x – 4y
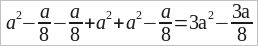
Поясним, например, 2-ой пример. Мы видим, что в этом многочлене слагаемое (+x) повторяется три раза. Мы можем, переставив члены многочлена, сделать так, чтобы эти три слагаемых оказались рядом; тогда сумму +x + x + x мы можем заменить одним членом, воспользовавшись коэффициентом +3, т. е. членом 3x. Далее мы получим, после указанной перестановки членов, четыре слагаемых, написанных рядом –y – y – y – y, мы можем, воспользовавшись коэффициентом –4, заменить эти 4 члена одним –4y.
Вот еще несколько примеров:
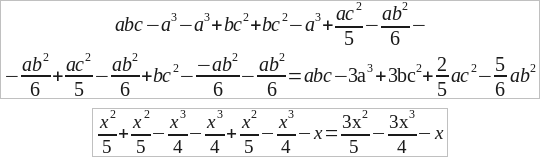
Рассмотрим далее пример:
a – 2b + 3a – b + a – 3b
Зная значения коэффициентов, имеющихся у некоторых членов этого многочлена, мы могли бы заменить второй член этого многочлена –2b через –b – b, третий член +3a через +a + a + a и последний член –3b через –b – b – b, и тогда мы увидали бы,что во всем многочлене a повторяется слагаемым 5 раз, что можно выразить коэффициентом +5, –b повторяется слагаемым 6 раз, что можно выразить коэффициентом –6 при множителе b, т. е.
a – 2b + 3a – b + a – 3b = 5a – 6b
Также
x + 9x – y – 7y + 11x – 2y + 4x = 25x – 10y
a³ – 3a² + 14a³ – 2a² = 15a³ – 5a²
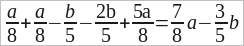 и т. п.
и т. п.
Пусть теперь имеем двучлен
5a – 8a
Зная значение коэффициентов, мы видим, что
5a – 8a = a + a + a + a + a – a – a – a – a – a – a – a – a
Так как известно, что +a и –a взаимно уничтожаются (или +a – a = 0), то предыдущая сумма сведется к –a – a – a или к –3a, т. е.
5a – 8a = –3a
Также
5x – 2x = x + x + x + x + x – x – x = 3x.
Возьмем теперь многочлен
12a – 4b – 3c + 4a + 7b – 2c – 6a – 4b + 5c.
Мы видим, что здесь сначала +a повторяется слагаемым 12 раз, затем 4 раза, а затем –a повторяется слагаемым 6 раз. Так как –6a взаимно уничтожаются c +6a, то остается после этого +a, повторенное слагаемым 10 раз, т. е. получим член +10a.
Также члены –4b + 7b – 4b вместе дадут лишь член –b, а члены –3c – 2c + 5c взаимно уничтожатся. Поэтому
2a – 4b – 3c + 4a + 7b – 2c – 6a – 4b + 5c= 10a – b.
Те упрощения многочленов, какие имели место в ряде предыдущих примеров, называются приведением подобных членов многочлена. Смысл этого преобразования состоит в том, что мы можем в одном многочлене те члены, буквенные множители которых совершенно одинаковы, заменять одним членом.
Эти члены, о которых здесь идет речь, имеющие одинаковых буквенных множителей, называются подобными членами. Так, 3a²b³ и –5a²b³ суть подобные члены и их можно, если они являются членами одного многочлена, заменить одним членом, но члены 3a³b и –5a²b не суть подобные, ибо их буквенные множители не одинаковы: у первого члена есть буквенный множитель a³, а у второго имеется множитель a², но не a³, и эти два члена, если они даже являются членами одного многочлена, нельзя соединить в один член.
Соединение подобных членов многочлена в один член и называется приведением подобных членов многочлена.
Чтобы научиться быстрее выполнять это преобразование, рассмотрим следующие 4 основных примера:
1) 12ab² + 23ab²
2) –7a³b² – 8a³b²
3) 12a²b – 7a²b
4) 6a²b² – 11a²b²
Зная значение входящих сюда коэффициентов, мы найдем результаты:
12ab² + 23ab² = 35ab²
–7a³b² – 8a³b² = –15a³b²
12a²b – 7a²b = 5a²b
6a²b² – 11a²b² = –5a²b²
Рассматривая эти результаты, мы прежде всего видим, что при приведении подобных членов буквенные множители остаются неизменными. Далее в 1-м примере у двух подобных членов были коэффициенты +12 и +23, а у результата получился коэф. +35. Ясно, что пришлось коэффициенты приводимых подобных членов сложить, также точно во 2-м примере были коэффициенты –7 и –8, а в результате коэф. = –15. Здесь также пришлось выполнить сложение (абсолютные величины сложить и приписать общий знак). В 3-м примере были коэффициенты +12 и –7, а у результата получился коэффициент +5, в 4-м из коэффиц. +6 и –11 получился коэффиц. –5. Вспоминая, что при сложении относительных чисел надо абсолютные их величины вычитать арифметически (из большей меньшую) и брать знак того числа, у которого абсолютная величина больше, мы придем к заключению, что и в этих случаях коэффициенты приходится складывать. Дело не меняется, если коэффициенты возьмем дробные. Итак,
чтобы выполнить приведение подобных членов многочлена (другими словами: чтобы все подобные члены одного многочлена соединить в один), надо сложить их коэффициенты, а буквенные множители оставить без изменения.
Конечно, если в многочлене 3 или более подобных членов, то можно выполнять сложение их коэффициентов в любом порядке.
Примеры:

Здесь для удобства подобные члены подчеркнуты одинаковыми знаками.
